Пусть 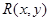 — рациональная функция своих аргументов.
— рациональная функция своих аргументов.
1) Интегралы вида 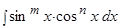 , где m и n - целые числа.
, где m и n - целые числа.
Рассмотрим два случая:
а) Среди чисел m, n есть хотя бы одно нечетное. Тогда отделяем от нечетной степени один сомножитель и выражаем с помощью формулы 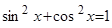 оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.
оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.
Пример. 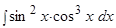 .
.
Решение.
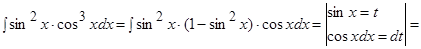
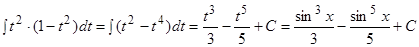 .
.
б) Оба числа m, n- четные неотрицательные.
Применим формулы:
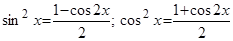 .
.
Пример. 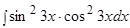 .
.
Решение.
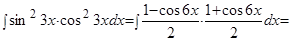
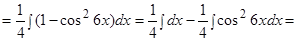
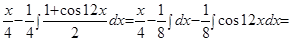
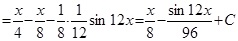 .
.
2) Интегралы вида 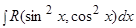 , где
, где 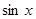 и
и 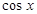 входят в подынтегральную рациональную функцию, только в четных степенях.
входят в подынтегральную рациональную функцию, только в четных степенях.
Делается замена: 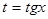 .
.
При этом 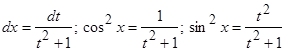 .
.
Пример. 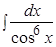 .
.
Решение.
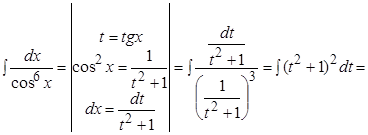
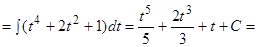
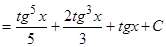 .
.
3) Интегралы вида 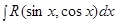 , где
, где 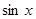 и
и 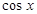 входят в подынтегральную рациональную функцию в нечетных степенях.
входят в подынтегральную рациональную функцию в нечетных степенях.
Делается универсальная тригонометрическая подстановка: 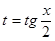 . В результате сводится к интегралу от рациональной дроби.
. В результате сводится к интегралу от рациональной дроби.
При этом 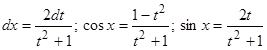 .
.
Пример. 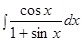 .
.
Решение.
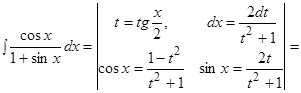
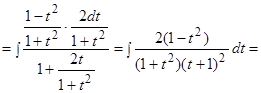
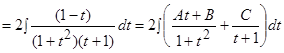 .
.
Приводим к общему знаменателю подынтегральную функцию. А поскольку дроби равны и их знаменатели равны, то равны и числители:
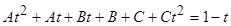 .
.
Два многочлена равны, когда равны коэффициенты при соответствующих степенях:
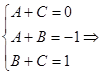
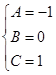 .
.
Получаем:
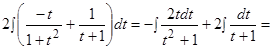
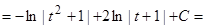
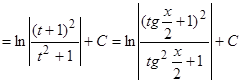 .
.





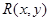 — рациональная функция своих аргументов.
— рациональная функция своих аргументов.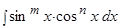 , где m и n - целые числа.
, где m и n - целые числа.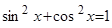 оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.
оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.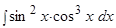 .
.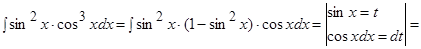
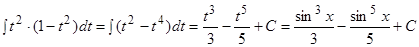 .
.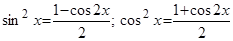 .
.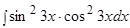 .
.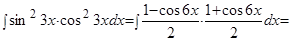
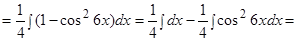
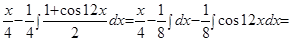
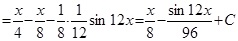 .
.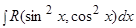 , где
, где 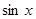 и
и 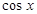 входят в подынтегральную рациональную функцию, только в четных степенях.
входят в подынтегральную рациональную функцию, только в четных степенях.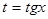 .
.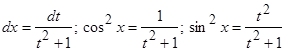 .
.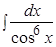 .
.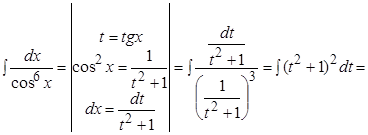
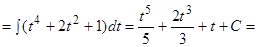
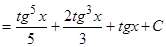 .
.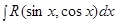 , где
, где 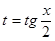 . В результате сводится к интегралу от рациональной дроби.
. В результате сводится к интегралу от рациональной дроби.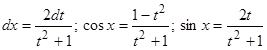 .
.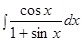 .
.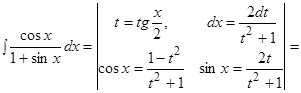
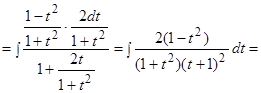
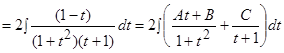 .
.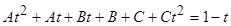 .
.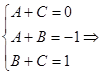
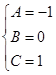 .
.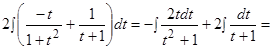
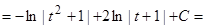
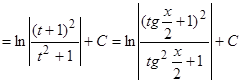 .
.


