Задание 1. Непосредственное интегрирование.
Непосредственное интегрирование предполагает использование свойств неопределенного интеграла, таблицы интегралов и различных формул из элементарной математики.
Пример. 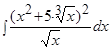 .
.
Решение. Воспользуемся формулой сокращенного умножения (квадрат суммы), свойствами степеней, свойствами 3-4 и формулой 1 таблицы интегралов:
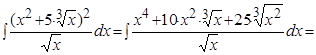
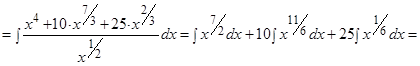
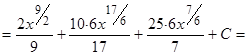

Пример. 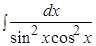 .
.
Решение. Преобразуем подынтегральную функцию:
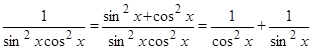 .
.
Следовательно, используя формулы 7 и 8 таблицы интегралов, получим:
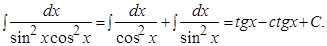
Пример. 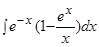 .
.
Решение. Преобразуем подынтегральную функцию, раскрыв скобки, и воспользуемся формулами 2 и 4 таблицы интегралов:
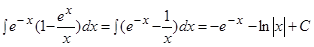 .
.
Задание 2. Интегралы с квадратным трехчленом.
Интегралы с квадратным трехчленом - это интегралы вида: 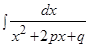 ,
, 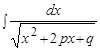 ,
, 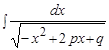 .
.
Для вычисления этих интегралов необходимо выделить в квадратных трехчленах знаменателей полный квадрат. В первых двух случаях квадратный трехчлен перепишется в виде: 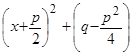 , в третьем случае он будет иметь вид:
, в третьем случае он будет иметь вид: 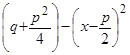 . В результате интегралы сводятся к табличным интегралам.
. В результате интегралы сводятся к табличным интегралам.
Замечание. Если коэффициент при 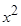 в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.
в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.
Пример. 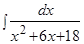 .
.
Решение. Выделим полный квадрат в знаменателе и воспользуемся формулой 10 таблицы интегралов:
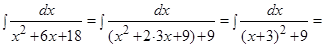
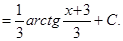
Пример. 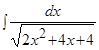 .
.
Решение. Выделим полный квадрат в подкоренном выражении и воспользуемся формулой 14 таблицы интегралов: 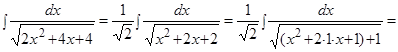
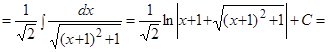
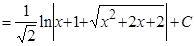 .
.
Пример . 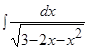 .
.
Решение. Выделим полный квадрат в подкоренном выражении и воспользуемся формулой 12 таблицы интегралов:
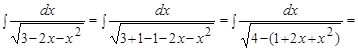
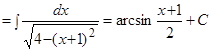 .
.
Задание 3. Замена переменной.
Пусть требуется найти интеграл с непрерывной подынтегральной функцией 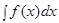 .
.
Сделаем замену переменных, положив 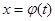 , где функция
, где функция 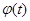 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям:
1) 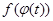 - непрерывная функция;
- непрерывная функция;
2) 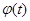 - непрерывно дифференцируемая функция, имеющая обратную функцию.
- непрерывно дифференцируемая функция, имеющая обратную функцию.
Тогда 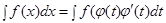 .
.
После интегрирования возвращаются к старой переменной обратной подстановкой.
Пример. 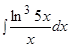 .
.
Решение.
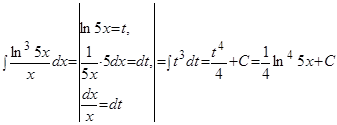 .
.
Пример. 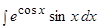 .
.
Решение.
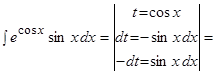
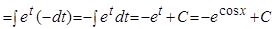 .
.
Пример. 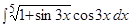 .
.
Решение.
Полагая 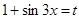 и продифференцировав обе части этого равенства, получаем:
и продифференцировав обе части этого равенства, получаем:
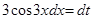 или
или 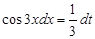 .
.
Тогда первоначальный интеграл равен:
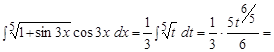
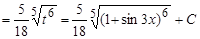 .
.
Пример. 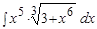 .
.
Решение.
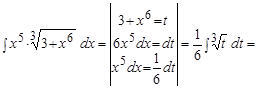
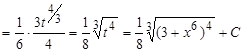 .
.
Задание 4. Интегрирование по частям.
Интегрированием по частям называется нахождение интеграла по формуле:
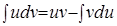 ,
,
где 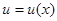
 и
и 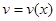 — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от 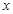 . С помощью этой формулы нахождение интеграла
. С помощью этой формулы нахождение интеграла 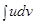 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 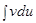 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
Применяется формула в следующих случаях:
1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию.
Это интегралы вида: 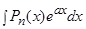 ,
, 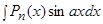 ,
, 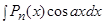 .
.
В этом случае в качестве 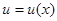 выбирается многочлен
выбирается многочлен 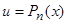 .
.
Пример. 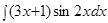 .
.
Решение. Подынтегральная функция есть произведение многочлена на тригонометрическую функцию (1 случай). Поэтому в качестве 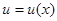 выбирается многочлен.
выбирается многочлен.
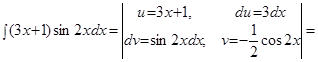
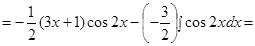
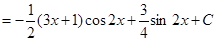 .
.
2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию.
Это интегралы вида: 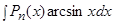 ,
, 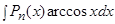 ,
, 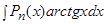 ,
, 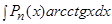 ,
, 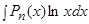 .
.
В качестве 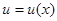 следует принимать обратную тригонометрическую или логарифмическую функцию.
следует принимать обратную тригонометрическую или логарифмическую функцию.
Пример. 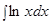 .
.
Решение. Подынтегральная функция есть логарифмическая функция (2 случай). Поэтому в качестве 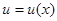 выбирается логарифмическая функция.
выбирается логарифмическая функция.
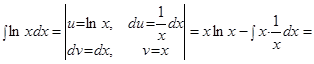
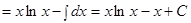 .
.
3) Интегралы вида: 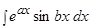 ,
, 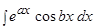 .
.
Метод интегрирования по частям применяется два раза до появления исходного интеграла. Оба раза в качестве 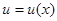 берем либо
берем либо 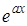 , либо тригонометрическую функцию. Получаем уравнение относительно исходного интеграла и решаем его.
, либо тригонометрическую функцию. Получаем уравнение относительно исходного интеграла и решаем его.
Пример. 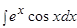 .
.
Решение. Это интеграл вида: 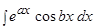 (3 случай). Поэтому в качестве
(3 случай). Поэтому в качестве 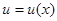 выберем
выберем 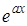 .
.
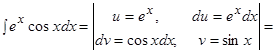
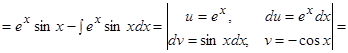
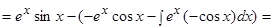
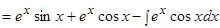 .
.
Обозначим исходный интеграл 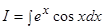 .
.
Получим уравнение:
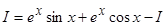 ;
;
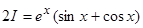 ;
;
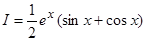 .
.
Таким образом, 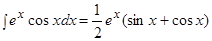 .
.
В некоторых случаях метод интегрирования по частям надо применять неоднократно.
Пример. 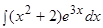 .
.
Решение.
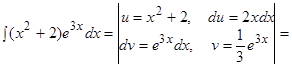
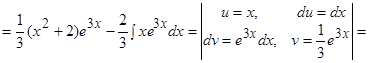
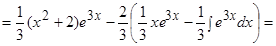
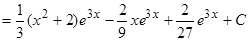 .
.





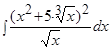 .
.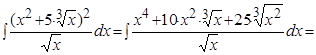
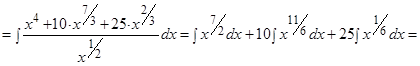
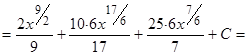

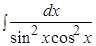 .
.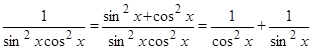 .
.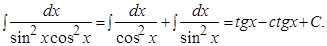
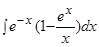 .
.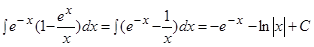 .
.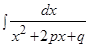 ,
, 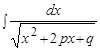 ,
, 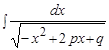 .
.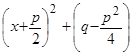 , в третьем случае он будет иметь вид:
, в третьем случае он будет иметь вид: 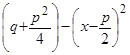 . В результате интегралы сводятся к табличным интегралам.
. В результате интегралы сводятся к табличным интегралам.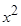 в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.
в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.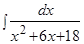 .
.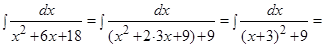
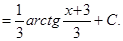
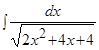 .
.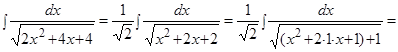
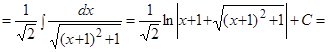
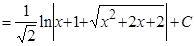 .
.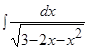 .
.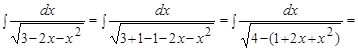
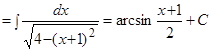 .
. 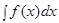 .
.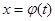 , где функция
, где функция 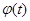 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям: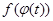 - непрерывная функция;
- непрерывная функция;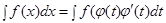 .
.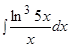 .
.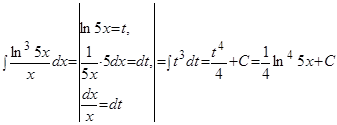 .
.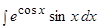 .
.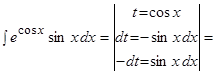
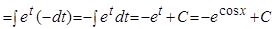 .
.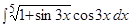 .
.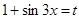 и продифференцировав обе части этого равенства, получаем:
и продифференцировав обе части этого равенства, получаем: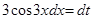 или
или 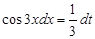 .
.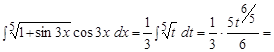
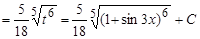 .
.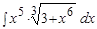 .
.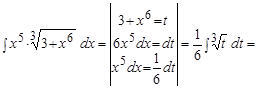
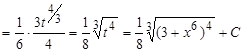 .
.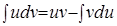 ,
,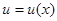
 и
и 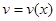 — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от 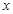 . С помощью этой формулы нахождение интеграла
. С помощью этой формулы нахождение интеграла 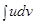 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 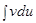 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.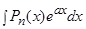 ,
, 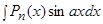 ,
, 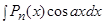 .
.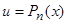 .
.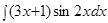 .
.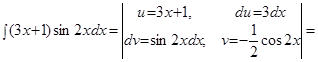
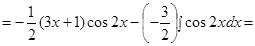
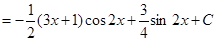 .
.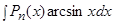 ,
, 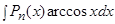 ,
, 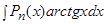 ,
, 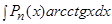 ,
, 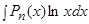 .
.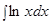 .
.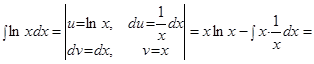
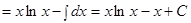 .
.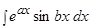 ,
, 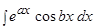 .
. 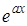 , либо тригонометрическую функцию. Получаем уравнение относительно исходного интеграла и решаем его.
, либо тригонометрическую функцию. Получаем уравнение относительно исходного интеграла и решаем его.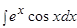 .
.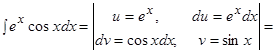
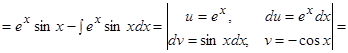
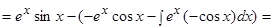
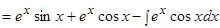 .
.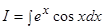 .
.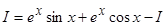 ;
;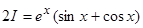 ;
;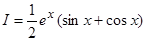 .
.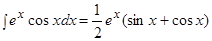 .
.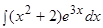 .
.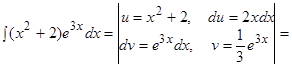
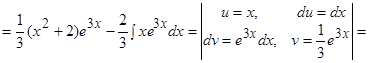
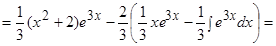
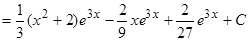 .
.


