Выражения вида 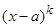 ;
; 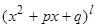 , где а - вещественное, k,l - натуральные числа, а квадратный трехчлен
, где а - вещественное, k,l - натуральные числа, а квадратный трехчлен 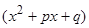 не имеет действительных корней, назовем простейшими сомножителями.
не имеет действительных корней, назовем простейшими сомножителями.
Известна основная теорема алгебры: любой многочлен 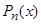 степени n можно разложить в произведение простейших сомножителей:
степени n можно разложить в произведение простейших сомножителей:
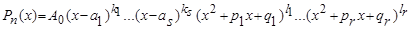 ,
,
где 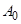 - число;
- число; 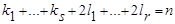 .
.
Дроби вида 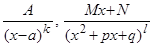 , где k, l - натуральные числа,
, где k, l - натуральные числа, 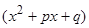 - простейший сомножитель, будем называть простейшими рациональными дробями.
- простейший сомножитель, будем называть простейшими рациональными дробями.
Дробь 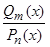 называется правильной, если
называется правильной, если 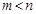 (m и nстепени многочленов, стоящих в числителе и в знаменателе, соответственно). Если
(m и nстепени многочленов, стоящих в числителе и в знаменателе, соответственно). Если 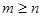 , дробь называется неправильной.
, дробь называется неправильной.
Каждую неправильную дробь можно представить в виде суммы многочлена и правильной дроби: 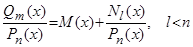 .
.
Теорема. Любая правильная рациональная дробь 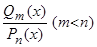 может быть представлена в виде суммы простейших рациональных дробей.
может быть представлена в виде суммы простейших рациональных дробей.
Эта сумма строится следующим образом в два этапа:
1) каждый простейший множитель вида 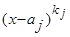 порождает следующую сумму из
порождает следующую сумму из 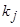 слагаемых:
слагаемых:
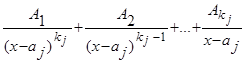 ;
;
2) каждый сомножитель вида 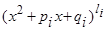 порождает следующую сумму из
порождает следующую сумму из 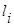 слагаемых:
слагаемых:
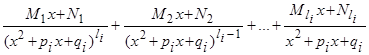 .
.
В результате мы получим следующее разложение правильной дроби на простейшие:
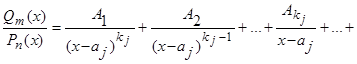
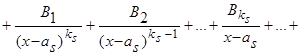
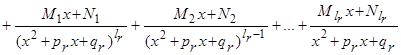 .
.
Пример. Разложить дробь 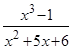 на простейшие дроби.
на простейшие дроби.
Решение. Так как дробь является неправильной, то сначала выделим целую часть (для этого достаточно найти частное и остаток от деления числителя на знаменатель):
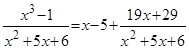 .
.
Разложим знаменатель на простейшие сомножители:
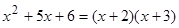 .
.
Тогда
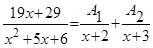 ;
;
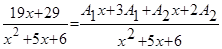 .
.
Две дроби, имеющие одинаковые знаменатели, равны, значит равны их числители:
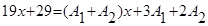 .
.
Два многочлена тождественно равны тогда, когда у них совпадают коэффициенты при одинаковых степенях 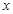 , следовательно, можно записать следующую систему уравнений:
, следовательно, можно записать следующую систему уравнений:
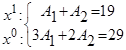 .
.
Решая ее, находим: 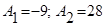 .
.
Окончательно получим: 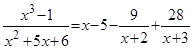 .
.
Из разложения следует, что интегрирование правильных рациональных дробей сводится к интегрированию простейших дробей.
Интегрирование простейших дробей:
I. 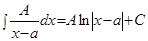 ;
;
II. 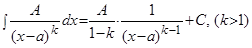 ;
;
III. 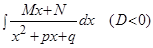 .
.
Этот интеграл вычисляется методом выделения полного квадрата.
IV. 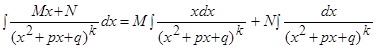 , квадратный трехчлен
, квадратный трехчлен 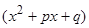 не имеет действительных корней.
не имеет действительных корней.
Первый интеграл берётся заменой:
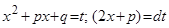 ,
,
второй интеграл вычисляется по формуле:
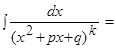
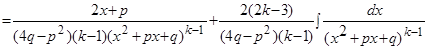 В результате получили формулу, в которой подынтегральное выражение имеет степень на единицу меньше. К нему вновь применяем ту же формулу пока не получим в знаменателе степень равную единице.
В результате получили формулу, в которой подынтегральное выражение имеет степень на единицу меньше. К нему вновь применяем ту же формулу пока не получим в знаменателе степень равную единице.
Пример. 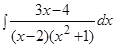 .
.
Решение. Подынтегральная дробь является правильной, так как степень многочлена в числителе меньше, чем в знаменателе. Разложим подынтегральное выражение на простейшие дроби:
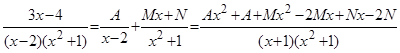 .
.
Составим систему уравнений для нахождения неизвестных коэффициентов:
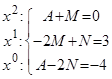 .
.
Отсюда 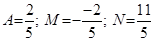 .
.
Следовательно, 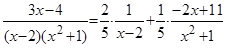 .
.
Теперь вычислим исходный интеграл:
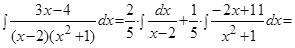
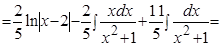
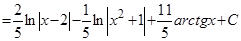 .
.
Пример.  .
.
Решение. Сначала разложим дробь на простейшие:
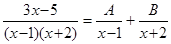 .
.
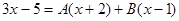 .
.
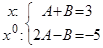 .
.
Решая систему, получим: 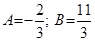 .
.
Тогда исходный интеграл примет вид:
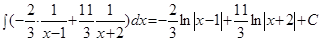 .
.
Пример. 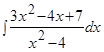 .
.
Решение. Так как дробь является неправильной, то сначала выделим целую часть. В результате получим:
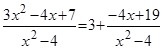 .
.
Теперь вычислим интеграл:
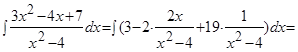
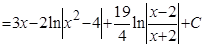 .
.
Пример. 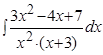 .
.
Решение. Подынтегральная дробь является правильной, так как степень многочлена в числителе меньше, чем в знаменателе. Разложим дробь на простейшие:
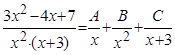 .
.
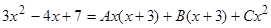 .
.
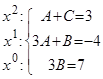 .
.
Решая систему, получим:  .
.
Тогда исходный интеграл примет вид:
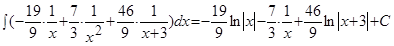 .
.





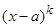 ;
; 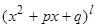 , где а - вещественное, k,l - натуральные числа, а квадратный трехчлен
, где а - вещественное, k,l - натуральные числа, а квадратный трехчлен 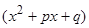 не имеет действительных корней, назовем простейшими сомножителями.
не имеет действительных корней, назовем простейшими сомножителями. степени n можно разложить в произведение простейших сомножителей:
степени n можно разложить в произведение простейших сомножителей: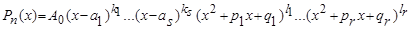 ,
,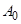 - число;
- число; 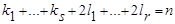 .
.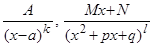 , где k, l - натуральные числа,
, где k, l - натуральные числа, 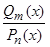 называется правильной, если
называется правильной, если 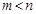 (m и nстепени многочленов, стоящих в числителе и в знаменателе, соответственно). Если
(m и nстепени многочленов, стоящих в числителе и в знаменателе, соответственно). Если 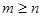 , дробь называется неправильной.
, дробь называется неправильной.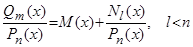 .
.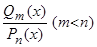 может быть представлена в виде суммы простейших рациональных дробей.
может быть представлена в виде суммы простейших рациональных дробей.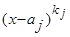 порождает следующую сумму из
порождает следующую сумму из 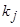 слагаемых:
слагаемых: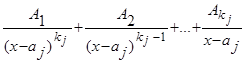 ;
;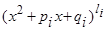 порождает следующую сумму из
порождает следующую сумму из 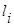 слагаемых:
слагаемых: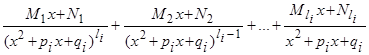 .
.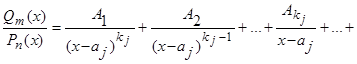
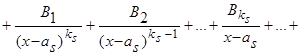
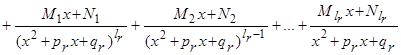 .
.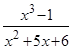 на простейшие дроби.
на простейшие дроби.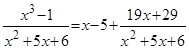 .
.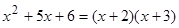 .
.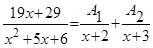 ;
;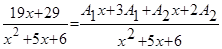 .
.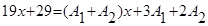 .
.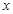 , следовательно, можно записать следующую систему уравнений:
, следовательно, можно записать следующую систему уравнений: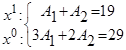 .
.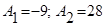 .
.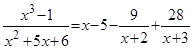 .
.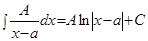 ;
;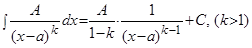 ;
;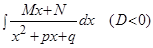 .
.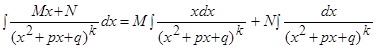 , квадратный трехчлен
, квадратный трехчлен 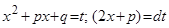 ,
,
 В результате получили формулу, в которой подынтегральное выражение имеет степень на единицу меньше. К нему вновь применяем ту же формулу пока не получим в знаменателе степень равную единице.
В результате получили формулу, в которой подынтегральное выражение имеет степень на единицу меньше. К нему вновь применяем ту же формулу пока не получим в знаменателе степень равную единице. .
. .
.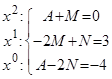 .
.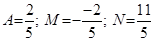 .
.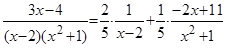 .
.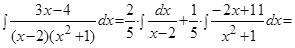
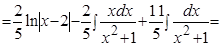
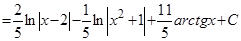 .
. .
.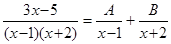 .
.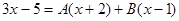 .
.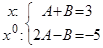 .
.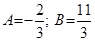 .
.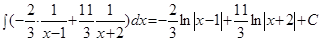 .
.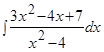 .
.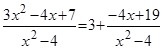 .
.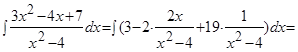
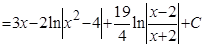 .
.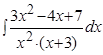 .
.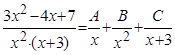 .
.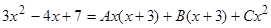 .
.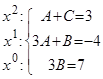 .
. .
.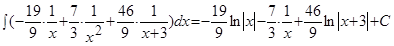 .
.


