Определенный интеграл и его приложения

Если 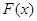 — некоторая первообразная функции 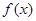, непрерывной на отрезке 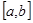, то определенный интеграл вычисляется по формуле Ньютона – Лейбница:

.

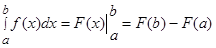Пример. .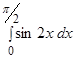

Решение.

.

 

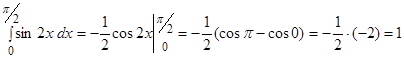Задание 8. Замена переменной.

Пусть выполняются следующие условия:

1) функция 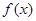 непрерывна на отрезке ;

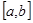2) функция 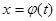 непрерывна вместе со своей производной 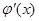на отрезке ;

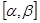3) , ;

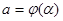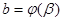4) функция 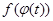 определена и непрерывна на отрезке .

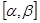Тогда .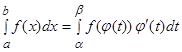

Пример. .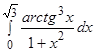

Решение.

.

 

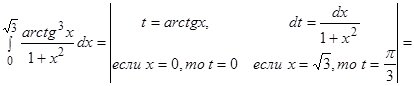
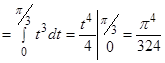Задание 9. Интегрирование по частям.

Определенный интеграл по частям вычисляется по формуле:

,

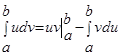где 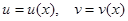 — непрерывно дифференцируемые функции на отрезке . Случаи, в которых следует применять интегрирование по частям, такие же, как в неопределенном интеграле.

Пример. .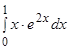

Решение.

.

 

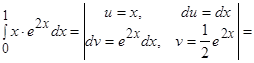
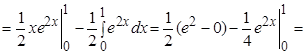
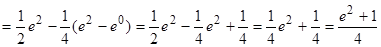Задание 10. Вычисление площади плоской фигуры, ограниченной линиями, заданными в декартовых координатах.

В декартовой системе координат элементарной фигурой является криволинейная трапеция (рис.1), ограниченная линиями 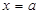, , 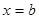, , 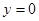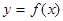площадь которой вычисляется по формуле:

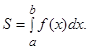
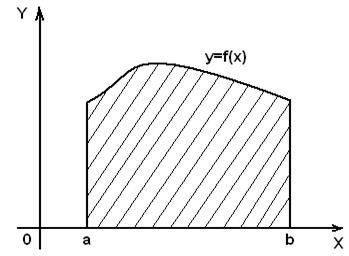
Рис.1

 

Площадь фигуры (рис.2) вычисляется по формуле:

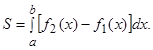
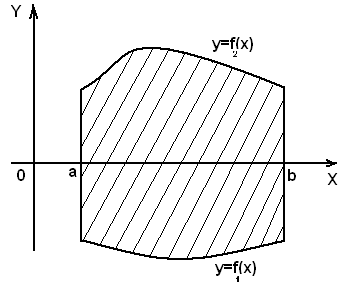
Рис.2

 

Пример. Найти площадь фигуры, ограниченной линиями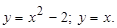

Решение. Построим чертеж к задаче (рис. 3).

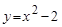 — это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));

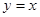 — прямая, проходящая через начало координат.

Найдем точки пересечения кривых. Для этого решим систему уравнений: .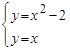

Отсюда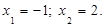

Площадь фигуры вычислим по формуле:

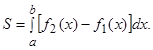
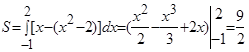(кв.ед.).

 

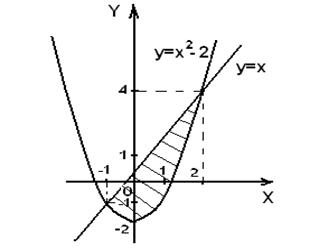
Рис. 3