Индуктивность 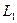 соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния
соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния 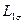 , индуктивность от части основного магнитного потока, созданной самой обмоткой
, индуктивность от части основного магнитного потока, созданной самой обмоткой 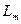 , и индуктивность от части основного потока, созданной двумя другими обмотками статора, равная
, и индуктивность от части основного потока, созданной двумя другими обмотками статора, равная 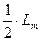 . Индуктивность
. Индуктивность 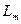 рассчитывается при отсутствии токов в других обмотках статора. Таким образом, полная индуктивность обмотки статора от основного магнитного потока одной обмотки статора и магнитных потоков двух других обмоток статора, равная
рассчитывается при отсутствии токов в других обмотках статора. Таким образом, полная индуктивность обмотки статора от основного магнитного потока одной обмотки статора и магнитных потоков двух других обмоток статора, равная 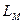 , в 3/2 раза больше ее индуктивности
, в 3/2 раза больше ее индуктивности 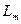 , рассчитанной при отсутствии токов в других обмотках.
, рассчитанной при отсутствии токов в других обмотках.
В силу симметрии статора, для других обмоток можно записать аналогичные выражения, а затем объединить фазные составляющие потокосцепления в обобщенный вектор потокосцепления статора при отсутствии токов ротора.
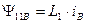 . (35)
. (35)
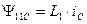 . (36)
. (36)
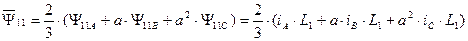 - обобщенный вектор потокосцепления статора АД.
- обобщенный вектор потокосцепления статора АД.
Наличие токов в обмотках ротора приведет к появлению дополнительных составляющих потокосцеплений обмоток статора. Если ось фазы «a» ротора смещена в пространстве на некоторый угол (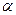 ), то взаимные индуктивности обмоток ротора и фазы «А» статора можно определить через соответствующие углы, образуемые их осями в виде –
), то взаимные индуктивности обмоток ротора и фазы «А» статора можно определить через соответствующие углы, образуемые их осями в виде – 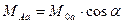 , (37)
, (37)
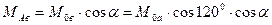 , (38)
, (38)
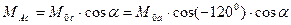 , (39)
, (39)
где 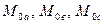 – взаимные индуктивности при (
– взаимные индуктивности при (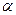 ) =0. Тогда «полное» потокосцепление обмотки фазы «А» статора при наличии токов ротора (т.е. потокосцепление обмотки статора в фазе «А» с магнитными потоками обмоток ротора) и с учетом того, что нулевой провод ротора отсутствует, будет равно
) =0. Тогда «полное» потокосцепление обмотки фазы «А» статора при наличии токов ротора (т.е. потокосцепление обмотки статора в фазе «А» с магнитными потоками обмоток ротора) и с учетом того, что нулевой провод ротора отсутствует, будет равно
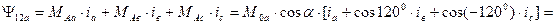
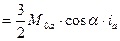 . (40)
. (40)
Но взаимная индуктивность обмотки фазы А статора и обмотки фазы «а» ротора при нулевом смещении осей 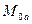 равна
равна 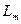 , т.к. параметры обмоток ротора приведены к статорным и приближенно можно считать, что при совпадении их осей картина магнитного поля будет такой же, как при совпадении осей статорных обмоток. Поэтому
, т.к. параметры обмоток ротора приведены к статорным и приближенно можно считать, что при совпадении их осей картина магнитного поля будет такой же, как при совпадении осей статорных обмоток. Поэтому 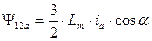 . (41)
. (41)
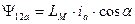 . (42)
. (42)
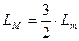 . (43)
. (43)
Аналогично можно получить для других потокосцеплений взаимной индуктивности обмоток фазы В и С статора и обмоток ротора.
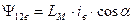 . (44)
. (44)
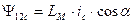 . (45)
. (45)
Объединяя уравнения (42), (44), (45), получим выражение для вектора обобщенного потокосцепления обмоток статора с магнитными потоками обмоток ротора.
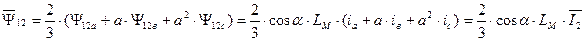 .
.
 . (46)
. (46)
Объединяя потокосцепления фазных обмоток статора 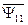 (с потоками статора) и
(с потоками статора) и 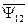 (с потоками ротора) в обобщенный вектор потокосцепления, получим
(с потоками ротора) в обобщенный вектор потокосцепления, получим
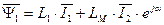 . (47)
. (47)
Аналогичное выражение, в силу симметрии связей между статором и ротором, можно записать для вектора обобщенного потокосцепления ротора.
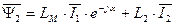 . (48)
. (48)
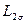 - индуктивность рассеяния роторной обмотки;
- индуктивность рассеяния роторной обмотки;
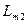 - индуктивность основного потока роторной обмотки.
- индуктивность основного потока роторной обмотки.
 - полная индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз.
- полная индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз.
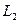 - результирующая индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз и магнитного потока рассеяния роторной обмотки.
- результирующая индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз и магнитного потока рассеяния роторной обмотки.
В выражениях (47) и (48) для потокосцеплений 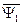 и
и  векторы тока статора и ротора записаны в различных системах координат. Так в выражении для потокосцепления
векторы тока статора и ротора записаны в различных системах координат. Так в выражении для потокосцепления 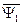 ток статора записан в неподвижной системе координат «
ток статора записан в неподвижной системе координат «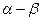 », связанной со статором, а ток ротора во вращающейся системе координат «
», связанной со статором, а ток ротора во вращающейся системе координат «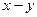 », связанной с ротором (смещенной на текущий угол «
», связанной с ротором (смещенной на текущий угол «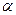 »). Полная запись выражений для потокосцеплений
»). Полная запись выражений для потокосцеплений 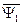 и
и  с учетом индексов систем координат выглядит следующим образом.
с учетом индексов систем координат выглядит следующим образом.
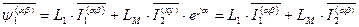 . (49)
. (49)
 . (49а)
. (49а)
В уравнениях (49) и (49а) имеют дело с переменными коэффициентами 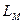 , зависящими от взаимного расположения обмоток статора и ротора.
, зависящими от взаимного расположения обмоток статора и ротора.
13.8. Особенности, свойства и преобразования «обобщенного» вектора и уравнений с «обобщенным» вектором
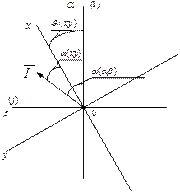 Если вектор тока представлен в неподвижной системе координат «
Если вектор тока представлен в неподвижной системе координат «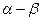 », то переход к новой системе координат «
», то переход к новой системе координат «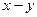 », развернутой относительно исходной на некоторый угол
», развернутой относительно исходной на некоторый угол 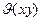 осуществляется из соотношения аргументов комплексных чисел. Новая система координат «x-y» может вращаться с постоянной скоростью
осуществляется из соотношения аргументов комплексных чисел. Новая система координат «x-y» может вращаться с постоянной скоростью 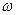 .
.
Рис. 10. Вектор обобщенного тока в двух системах координат
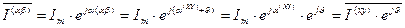 . (50)
. (50)
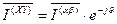 . (51)
. (51)
 . (52)
. (52)
При этом следует заметить, что на угол 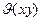 не накладывается никаких ограничений, т.е. он может иметь постоянное значение, но
не накладывается никаких ограничений, т.е. он может иметь постоянное значение, но 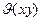 может также изменяться произвольным образом. Обобщенный вектор можно представить также во вращающейся системе координат (
может также изменяться произвольным образом. Обобщенный вектор можно представить также во вращающейся системе координат (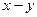 ). Для системы координат (
). Для системы координат (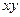 ), вращающейся с постоянной угловой частотой
), вращающейся с постоянной угловой частотой 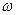 угол
угол 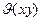 равен
равен 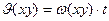 .
.
Преобразование координат можно осуществить не только от неподвижной системы к вращающейся, но и для двух систем координат, вращающихся с различными угловыми частотами.
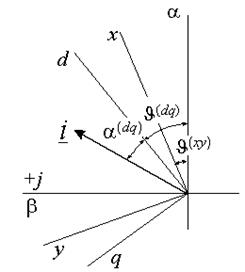
Рис. 11. Вектор обобщенного тока в трех системах координат, две из которых вращаются
Пусть вектор 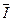 представлен в системе координат «
представлен в системе координат «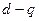 », текущий угол которой относительно неподвижных координат составляет
», текущий угол которой относительно неподвижных координат составляет 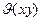 . Тогда из соотношений углов преобразование координат можно записать в виде
. Тогда из соотношений углов преобразование координат можно записать в виде
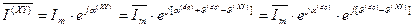 . (53)
. (53)
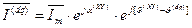 . (54)
. (54)





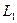 соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния
соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния 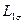 , индуктивность от части основного магнитного потока, созданной самой обмоткой
, индуктивность от части основного магнитного потока, созданной самой обмоткой 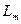 , и индуктивность от части основного потока, созданной двумя другими обмотками статора, равная
, и индуктивность от части основного потока, созданной двумя другими обмотками статора, равная 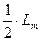 . Индуктивность
. Индуктивность 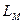 , в 3/2 раза больше ее индуктивности
, в 3/2 раза больше ее индуктивности 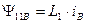 . (35)
. (35)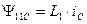 . (36)
. (36)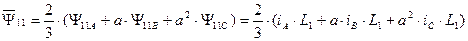 - обобщенный вектор потокосцепления статора АД.
- обобщенный вектор потокосцепления статора АД.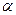 ), то взаимные индуктивности обмоток ротора и фазы «А» статора можно определить через соответствующие углы, образуемые их осями в виде –
), то взаимные индуктивности обмоток ротора и фазы «А» статора можно определить через соответствующие углы, образуемые их осями в виде – 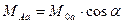 , (37)
, (37)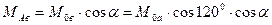 , (38)
, (38)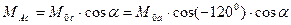 , (39)
, (39)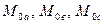 – взаимные индуктивности при (
– взаимные индуктивности при (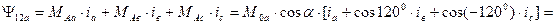
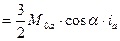 . (40)
. (40)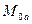 равна
равна 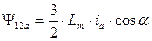 . (41)
. (41)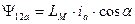 . (42)
. (42)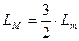 . (43)
. (43)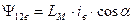 . (44)
. (44)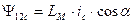 . (45)
. (45)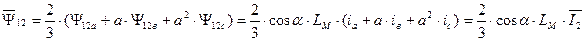 .
. . (46)
. (46)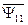 (с потоками статора) и
(с потоками статора) и 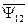 (с потоками ротора) в обобщенный вектор потокосцепления, получим
(с потоками ротора) в обобщенный вектор потокосцепления, получим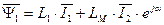 . (47)
. (47)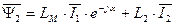 . (48)
. (48)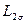 - индуктивность рассеяния роторной обмотки;
- индуктивность рассеяния роторной обмотки;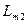 - индуктивность основного потока роторной обмотки.
- индуктивность основного потока роторной обмотки. - полная индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз.
- полная индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз.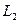 - результирующая индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз и магнитного потока рассеяния роторной обмотки.
- результирующая индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз и магнитного потока рассеяния роторной обмотки.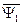 и
и  векторы тока статора и ротора записаны в различных системах координат. Так в выражении для потокосцепления
векторы тока статора и ротора записаны в различных системах координат. Так в выражении для потокосцепления 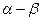 », связанной со статором, а ток ротора во вращающейся системе координат «
», связанной со статором, а ток ротора во вращающейся системе координат «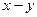 », связанной с ротором (смещенной на текущий угол «
», связанной с ротором (смещенной на текущий угол «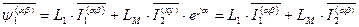 . (49)
. (49) . (49а)
. (49а)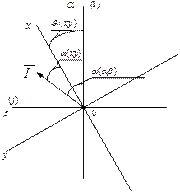 Если вектор тока представлен в неподвижной системе координат «
Если вектор тока представлен в неподвижной системе координат «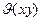 осуществляется из соотношения аргументов комплексных чисел. Новая система координат «x-y» может вращаться с постоянной скоростью
осуществляется из соотношения аргументов комплексных чисел. Новая система координат «x-y» может вращаться с постоянной скоростью 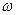 .
.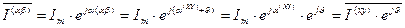 . (50)
. (50)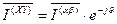 . (51)
. (51) . (52)
. (52)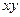 ), вращающейся с постоянной угловой частотой
), вращающейся с постоянной угловой частотой 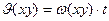 .
.
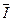 представлен в системе координат «
представлен в системе координат «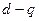 », текущий угол которой относительно неподвижных координат составляет
», текущий угол которой относительно неподвижных координат составляет 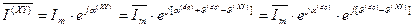 . (53)
. (53)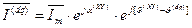 . (54)
. (54)

