Общие представления о математических моделях систем электропривода
Среди видов математического обеспечения САПР ЭП имеются математические модели элементов электропривода и математические модели систем электропривода.
Существуют следующие формы представления математических моделей:
1. форма уравнений состояния;
2. форма структурных схем;
Форма передаточной функции.
При разработке математической модели системы электропривода в первую очередь рассматривается функциональная схема системы и математические модели элементов электропривода. Примерная функциональная схема системы электропривода приведена на рис. 1.
Рис. 1. Функциональная схема системы электропривода с регуляторами положения, скорости и тока
Математическая модель системы ЭП, записанная в первой форме, представляет систему алгебраических и дифференциальных уравнений. Провести анализ такой математической модели системы ЭП – это значит решить эту систему алгебраических и дифференциальных уравнений. Общим методом решения систем дифференциальных уравнений является метод интегрирования этих дифференциальных уравнений.
Различают следующие методы интегрирования систем дифференциальных уравнений.
Аналитические методы.
Графические методы.
Графо – аналитические методы.
Численные методы.
В настоящее время графические и графо – аналитические методы практически не применяются. Аналитические методы используются при выполнении исследований с целью проведения анализа и получения общих выводов при решении теоретических задач. Численные методы применяются при решении большинства прикладных задач.
На рис. 2 приведена структурная схема системы электропривода с регулятором скорости.
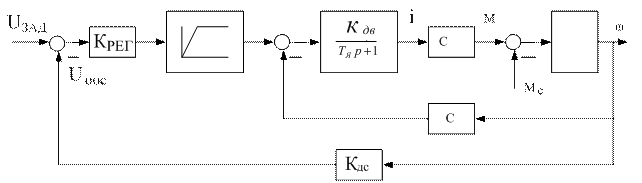
Рис. 2. Структурная схема системы электропривода с регулятором скорости
Пример математической модели системы электропривода
Для моделирования СЭП с применением структурной схемы (см. рис. 2.) используется структурный метод.
Различают реализацию структурного метода моделирования в стандартном варианте и нестандартном. Стандартный вариант предполагает использование современных программных пакетов, реализующих структурное моделирование. В нестандартном варианте используются классические традиционные программы по методу структурного моделирования, требующие подготовки рабочих подпрограмм, в которых обозначается связь между элементами структурной схемы. Оба варианта применимы к любым линейным и нелинейным системам управления.
Уравнения математической модели системы электропривода составляются на основе структурной схемы (см. рис. 2.).
Входное напряжение регулятора скорости (см. рис. 2) представляет собой ошибку регулирования и определяется как разность напряжений задания и датчика скорости.
 . (1)
. (1)
Выходной сигнал пропорционального регулятора скорости системы электропривода (СЭП) является напряжением управления силового преобразователя и вычисляется как произведение 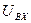 на коэффициент передачи регулятора.
на коэффициент передачи регулятора.
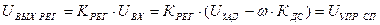 . (2)
. (2)
Силовой преобразователь (СП) на рис. 2 является безинерционным звеном и его выходное напряжение рассчитывается по выражению

 . (3)
. (3)
Уравнение для цепи якоря ЭД составлено по 2-му закону Кирхгофа.
 . (4)
. (4)
Уравнение состояния механической части СЭП запишем в форме равнения движения.
 . (5)
. (5)
Уравнения (4) и (5) преобразуем и после преобразования запишем в нормальной форме.
 . (6)
. (6)
 . (7)
. (7)
Для моделирования СЭП по уравнениям (1)-(3), (6) и (7) используется метод моделирования по уравнениям состояния.
Различают реализацию метода моделирования по уравнениям состояния в стандартном варианте и нестандартном. Стандартный вариант предполагает использование готовых программных пакетов, в которых реализуются современные методы численного интегрирования дифференциальных уравнений, и создаваемой пользователем рабочей подпрограммы, в которой запрограммированы уравнения СЭП, т.е. применительно к рис. 2. уравнения (1)-(3), (6) и (7) и нелинейная характеристика СП. В нестандартном варианте пользователь практически полностью программирует решение задачи моделирования СЭП по уравнениям состояния без обращения к рабочей подпрограмме. Оба варианта применимы к любым линейным и нелинейным системам управления.

Рис. 3. Характеристика управления СП, представленная по методу кусочно-линейной аппроксимации
Нелинейная характеристика управления СП имеет 2 участка.
Уравнение первого участка  соответствует пределам изменения напряжения управления от 0 до
соответствует пределам изменения напряжения управления от 0 до  . На втором участке характеристики управления СП напряжение на выходе не изменяется, т.е.
. На втором участке характеристики управления СП напряжение на выходе не изменяется, т.е.  при изменении
при изменении  .
.
Для нелинейной характеристики управления СП, представленной на рис. 4, уравнение первого участка определяется функцией синуса (см. уравнение (8), а на втором участке напряжение на выходе СП остается постоянным  .
.
 , (8)
, (8)
где 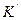 - фазовый коэффициент.
- фазовый коэффициент.

Рис. 4. Характеристика управления СП







 . (1)
. (1)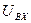 на коэффициент передачи регулятора.
на коэффициент передачи регулятора.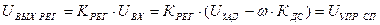 . (2)
. (2)
 . (3)
. (3) . (4)
. (4) . (5)
. (5) . (6)
. (6) . (7)
. (7)
 соответствует пределам изменения напряжения управления от 0 до
соответствует пределам изменения напряжения управления от 0 до  . На втором участке характеристики управления СП напряжение на выходе не изменяется, т.е.
. На втором участке характеристики управления СП напряжение на выходе не изменяется, т.е.  при изменении
при изменении  .
. , (8)
, (8)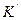 - фазовый коэффициент.
- фазовый коэффициент.


