Полная система уравнений идеальной жидкости включает, во-первых, универсальную систему, которая для идеальной жидкости имеет вид:
|
| 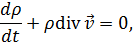
| Уравнение неразрывности
|
|
| 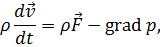
| Уравнение движения идеальной жидкости (уравнение Эйлера)
|
|
| 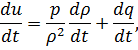
| Уравнение притока тепла
|
|
| 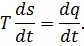
| Второй закон термодинамики
|
где 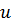 – плотность внутренней энергии;
– плотность внутренней энергии;
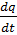 – приток тепла к единице массы за единицу времени;
– приток тепла к единице массы за единицу времени;
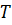 – температура;
– температура;
 – энтропия.
– энтропия.
Уравнение движения идеальной жидкости 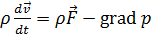 называется уравнением Эйлера.
называется уравнением Эйлера.
Обычно приток тепла 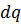 определяется законом Фурье, поэтому неизвестных в этой системе 8:
определяется законом Фурье, поэтому неизвестных в этой системе 8:
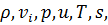
а уравнений – 6, следовательно, нужны еще 2 соотношения, которые определяют конкретную жидкость или газ. Эти два отношения называются уравнениями состояния. Обычно они представляют собой: 1) связь между давлением, плотностью и температурой, и 2) выражение плотности внутренней энергии как функции плотности и температуры, то есть следующие соотношения:
1) 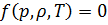 - уравнение состояния,
- уравнение состояния,
2) 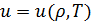 – калорическое уравнение состояния.
– калорическое уравнение состояния.
Рассмотрим различные уравнения состояния для жидкостей и газов.
В области нефтяной и газовой промышленности, преимущественно уравнение состояния описывает связь между плотностью флюида и давлением в виде 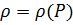 .
.
Для жидкостей при больших изменениях давления от начального значения P0 до текущего значения P плотность жидкости может быть определена по формуле:
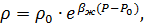
где 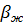 – объемный коэффициент упругости жидкости,
– объемный коэффициент упругости жидкости,
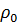 – плотность жидкости при давлении P0.
– плотность жидкости при давлении P0.
Так как значение выражения 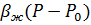 обычно много меньше единицы, то при разложении экспоненты в ряд Тейлора, ограничиваясь линейным приближением, можно записать уравнение состояния в виде
обычно много меньше единицы, то при разложении экспоненты в ряд Тейлора, ограничиваясь линейным приближением, можно записать уравнение состояния в виде
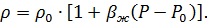
Данная форма записи обычно используется при определении плотности жидкости при малых изменениях давления P.
Для газов уравнение состояния играет очень важную роль в силу сильной сжимаемости. Самой простой моделью газа является совершенный газ.
Совершенным газом называется такой газ, в котором согласно молекулярно-кинетической теории выполнены следующие условия:
· Потенциальной энергией взаимодействия частиц газа можно пренебречь по сравнению с их кинетической энергией;
· Суммарный объем частиц газа пренебрежимо мал;
· Отсутствуют силы взаимодействия между частицами, а соударения частиц между собой и со стенками сосуда являются абсолютно упругими;
· Время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями.
Совершенный газ описывается уравнением состояния Менделеева-Клапейрона:
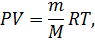
где 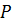 – давление;
– давление;
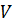 – объем;
– объем;
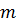 – масса;
– масса;
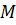 – молярная масса;
– молярная масса;
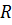 – универсальная газовая постоянная;
– универсальная газовая постоянная;
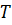 – температура.
– температура.
При изотермическом переходе газа из одного состояния в другое, уравнение состояния Менделеева-Клапейрона удобнее записать в виде:
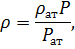
где 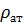 – плотность газа при атмосферном давлении
– плотность газа при атмосферном давлении 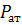 .
.
Примечание. В физике используется термин «идеальный газ». Однако в механике сплошных сред термины «идеальный газ» и «идеальная жидкость» заняты. Они означают, что касательные напряжения (вязкость) в этой модели не учитываются. Поэтому для газа, удовлетворяющего уравнению Менделеева-Клапейрона, вместо названия «идеальный газ», принятого в физике, используется название «совершенный газ» (perfect gas).
Использовать уравнение состояния совершенного газа целесообразно лишь при низких давлениях, так как в этом случае реальные газы согласуются с введенным определением совершенного газа. В случае высоких давлений и возможных фазовых переходах, использование уравнения состояния совершенного газа невозможно. В этом случае часто используют полуэмпирически выведенные уравнения состояния. Например, уравнения состояния Ван-дер-Ваальса, Дитеричи, Редлиха-Квонга, Пенга-Робинсона и другие.
Наиболее распространенной формой уравнения состояния для реальных газов является уравнение состояния Менделеева-Клапейрона с коэффициентом сверхсжимаемости z(P):
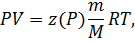
или в случае изотермического перехода
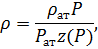
где z(P) характеризует степень отклонения реального газа от совершенного. Характерная зависимость коэффициента сжимаемости для углеводородной смеси в терминах приведенной температуры и давления представлена на рисунке 5.2.
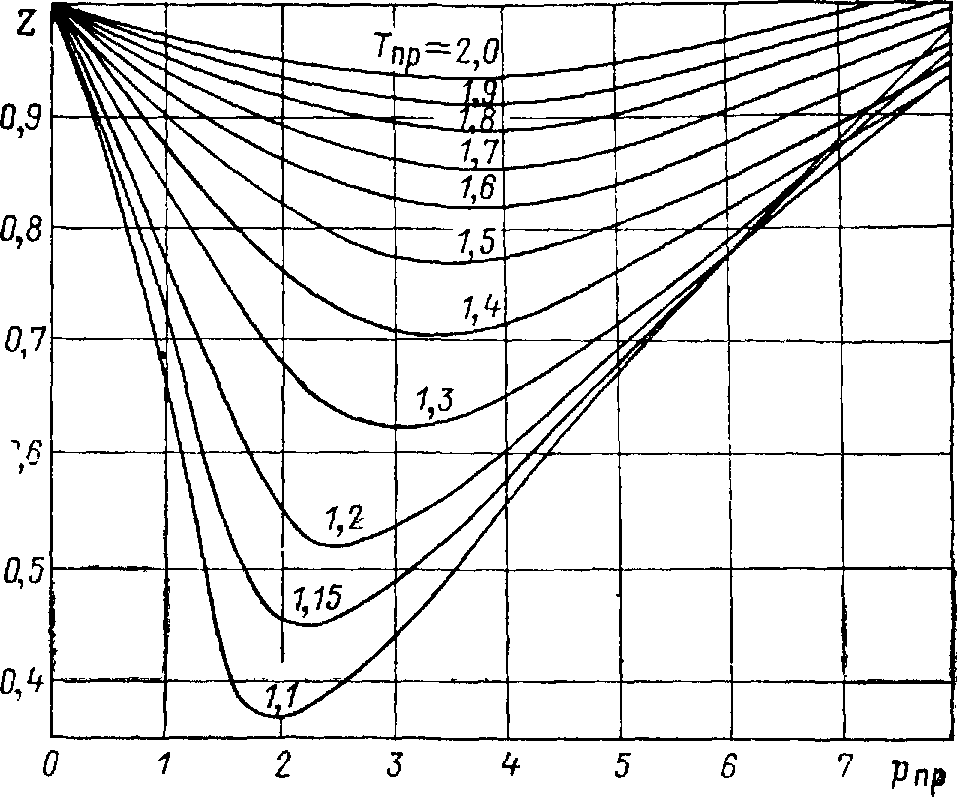
Рисунок 5.2 – Зависимость коэффициента сверхсжимаемости z(P) от приведенного давления
С молекулярно-кинетической точки зрения характер изменения коэффициента z(P) можно объяснить следующим образом. При малых значениях давления реальный и совершенный газ близки между собой, поэтому 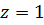 . Увеличение давления в системе ведет к увеличению плотности газа, а, следовательно, уменьшению расстояния между молекулами, что приводит к большей сжимаемости реального газа за счет проявления сил притяжения (которые отсутствуют в совершенном газе), объясняющее уменьшение значения z. Точка минимума на графике z(P) соответствует максимальной интенсивности проявления сил притяжение. Последующее увеличение давления и увеличение коэффициента z связано с сопротивлением газа сжатию, из-за проявления сил межмолекулярного отталкивания. Определение зависимости коэффициента сверхсжимаемости z от давления P является важной задачей, так как позволяет наиболее точно характеризовать газовую смесь и определить возможный момент конденсации газа в жидкое состояние.
. Увеличение давления в системе ведет к увеличению плотности газа, а, следовательно, уменьшению расстояния между молекулами, что приводит к большей сжимаемости реального газа за счет проявления сил притяжения (которые отсутствуют в совершенном газе), объясняющее уменьшение значения z. Точка минимума на графике z(P) соответствует максимальной интенсивности проявления сил притяжение. Последующее увеличение давления и увеличение коэффициента z связано с сопротивлением газа сжатию, из-за проявления сил межмолекулярного отталкивания. Определение зависимости коэффициента сверхсжимаемости z от давления P является важной задачей, так как позволяет наиболее точно характеризовать газовую смесь и определить возможный момент конденсации газа в жидкое состояние.





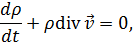
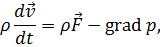
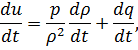
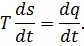
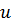 – плотность внутренней энергии;
– плотность внутренней энергии;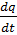 – приток тепла к единице массы за единицу времени;
– приток тепла к единице массы за единицу времени;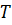 – температура;
– температура; – энтропия.
– энтропия.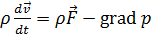 называется уравнением Эйлера.
называется уравнением Эйлера.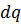 определяется законом Фурье, поэтому неизвестных в этой системе 8:
определяется законом Фурье, поэтому неизвестных в этой системе 8: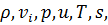
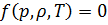 - уравнение состояния,
- уравнение состояния,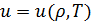 – калорическое уравнение состояния.
– калорическое уравнение состояния.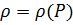 .
.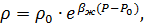
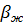 – объемный коэффициент упругости жидкости,
– объемный коэффициент упругости жидкости,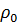 – плотность жидкости при давлении P0.
– плотность жидкости при давлении P0.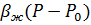 обычно много меньше единицы, то при разложении экспоненты в ряд Тейлора, ограничиваясь линейным приближением, можно записать уравнение состояния в виде
обычно много меньше единицы, то при разложении экспоненты в ряд Тейлора, ограничиваясь линейным приближением, можно записать уравнение состояния в виде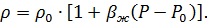
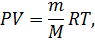
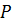 – давление;
– давление;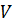 – объем;
– объем;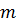 – масса;
– масса;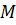 – молярная масса;
– молярная масса;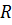 – универсальная газовая постоянная;
– универсальная газовая постоянная;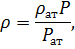
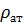 – плотность газа при атмосферном давлении
– плотность газа при атмосферном давлении 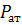 .
.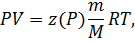
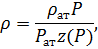

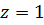 . Увеличение давления в системе ведет к увеличению плотности газа, а, следовательно, уменьшению расстояния между молекулами, что приводит к большей сжимаемости реального газа за счет проявления сил притяжения (которые отсутствуют в совершенном газе), объясняющее уменьшение значения z. Точка минимума на графике z(P) соответствует максимальной интенсивности проявления сил притяжение. Последующее увеличение давления и увеличение коэффициента z связано с сопротивлением газа сжатию, из-за проявления сил межмолекулярного отталкивания. Определение зависимости коэффициента сверхсжимаемости z от давления P является важной задачей, так как позволяет наиболее точно характеризовать газовую смесь и определить возможный момент конденсации газа в жидкое состояние.
. Увеличение давления в системе ведет к увеличению плотности газа, а, следовательно, уменьшению расстояния между молекулами, что приводит к большей сжимаемости реального газа за счет проявления сил притяжения (которые отсутствуют в совершенном газе), объясняющее уменьшение значения z. Точка минимума на графике z(P) соответствует максимальной интенсивности проявления сил притяжение. Последующее увеличение давления и увеличение коэффициента z связано с сопротивлением газа сжатию, из-за проявления сил межмолекулярного отталкивания. Определение зависимости коэффициента сверхсжимаемости z от давления P является важной задачей, так как позволяет наиболее точно характеризовать газовую смесь и определить возможный момент конденсации газа в жидкое состояние.


