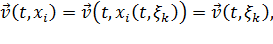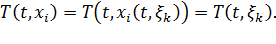При описании движения по Лагранжу мы следим за тем,что происходит в каждой индивидуальной частице среды.Частицы движутся, и приборы, измеряющие их параметры, следуют за каждой из них, например движутся вместе с ними (рис. 2.1а).
С точки зрения Лагранжа, мы интересуемся законами изменения скорости 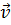 , температуры
, температуры 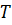 , давления
, давления  и других величин для данной индивидуальной точки среды:
и других величин для данной индивидуальной точки среды:
При описании движения по Эйлеру мы изучаем, что происходит в точках пространства, через которое движется среда. Обычно Эйлеров подход используется, когда нам не важно знать историю движения каждой индивидуальной частицы – где она была когда-то, куда попадет в будущем, а важно лишь знать, что происходит в данном месте.
Величины, характеризующие движение сплошной среды рассматриваются при эйлеровом подходе как функции пространственных координат 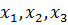 и времени
и времени 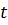 :
:
Лагранжев и эйлеров подходы к описанию движения среды схематически изображены на рисунке 2.1.
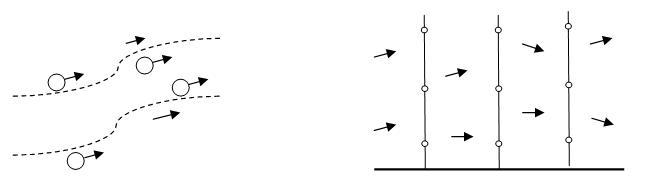
а) б)
Рисунок 2.1 – a) лагранжево описание: шары с измерительными приборами летят вместе с частицами воздуха; б) эйлерово описание: параметры воздушного потока измеряют приборы, помещенные на специальных мачтах
Переход от лагранжева описания к эйлерову
Пусть известны все параметры, описывающие движение, как функции времени и лагранжевых координат, то есть известны 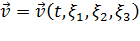 ,
, 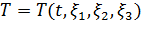 и т.д. В частности, известен закон движения
и т.д. В частности, известен закон движения
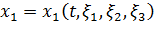 ,
,
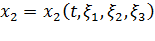 ,
,
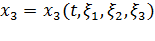 .
.
Найдем из этих соотношений 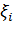 как функции от
как функции от 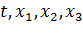 :
:
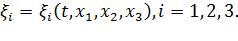
Подставляя эти выражения в функции 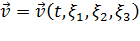 ,
, 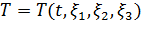 и т.д., найдем скорость, температуру и другие параметры как функции пространственных координат и времени, то есть в эйлеровом описании:
и т.д., найдем скорость, температуру и другие параметры как функции пространственных координат и времени, то есть в эйлеровом описании:
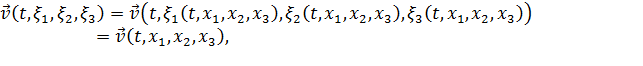
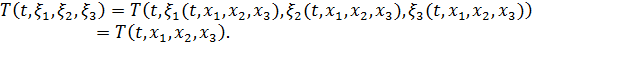
Переход от эйлерова описания к лагранжеву
Пусть нам известно все с точки зрения Эйлера. В частности, известны скорости среды во всех точках 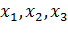 во все моменты времени
во все моменты времени  , то есть известна функция
, то есть известна функция 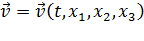 . Как найти закон движения? Как ввести лагранжевы координаты?
. Как найти закон движения? Как ввести лагранжевы координаты?
По определению, компоненты скорости каждой точки равны производным по времени от пространственных координат точки:
Эти соотношения представляют собой системы обыкновенных дифференциальных уравнений для нахождения  , как функций времени. Для нахождения решения необходимо задать значения
, как функций времени. Для нахождения решения необходимо задать значения  в начальный момент времени. Если при
в начальный момент времени. Если при  задано, что
задано, что 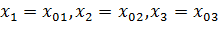 , то решение записывается в виде:
, то решение записывается в виде:
Это и есть закон движения (2.2). Начальные координаты 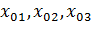 можно взять в качестве лагранжевых координат. Вводя обозначения
можно взять в качестве лагранжевых координат. Вводя обозначения 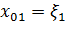 ,
, 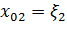 ,
, 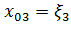 , будем иметь
, будем иметь 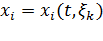 , где для краткости через
, где для краткости через 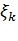 обозначен набор
обозначен набор 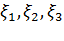 . Подставляя полученные выражения для
. Подставляя полученные выражения для 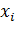 в функции
в функции 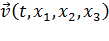 ,
, 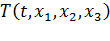 и т.д., получим интересующие нас параметры как функции времени и лагранжевых координат, то есть в лагранжевом описании:
и т.д., получим интересующие нас параметры как функции времени и лагранжевых координат, то есть в лагранжевом описании:





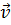 , температуры
, температуры 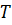 , давления
, давления  и других величин для данной индивидуальной точки среды:
и других величин для данной индивидуальной точки среды: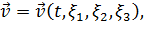
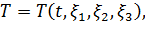
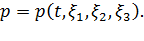
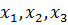 и времени
и времени 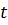 :
: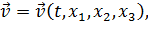
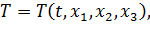
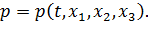

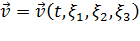 ,
, 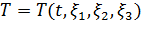 и т.д. В частности, известен закон движения
и т.д. В частности, известен закон движения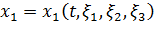 ,
,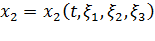 ,
,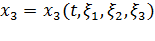 .
.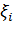 как функции от
как функции от 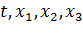 :
: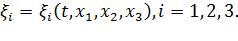
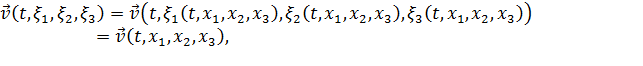
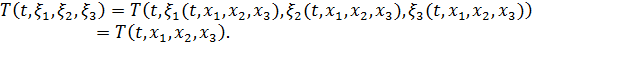
 во все моменты времени
во все моменты времени  , то есть известна функция
, то есть известна функция 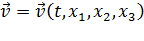 . Как найти закон движения? Как ввести лагранжевы координаты?
. Как найти закон движения? Как ввести лагранжевы координаты?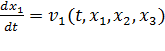 ,
,
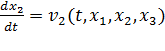 ,
,
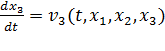 .
.
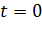 задано, что
задано, что 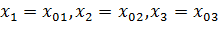 , то решение записывается в виде:
, то решение записывается в виде: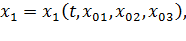
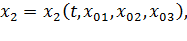
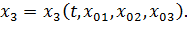
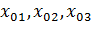 можно взять в качестве лагранжевых координат. Вводя обозначения
можно взять в качестве лагранжевых координат. Вводя обозначения 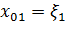 ,
, 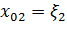 ,
, 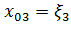 , будем иметь
, будем иметь 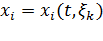 , где для краткости через
, где для краткости через 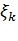 обозначен набор
обозначен набор 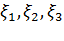 . Подставляя полученные выражения для
. Подставляя полученные выражения для 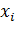 в функции
в функции 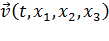 ,
, 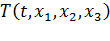 и т.д., получим интересующие нас параметры как функции времени и лагранжевых координат, то есть в лагранжевом описании:
и т.д., получим интересующие нас параметры как функции времени и лагранжевых координат, то есть в лагранжевом описании: