Тензор скоростей деформаций. Вектор вихря

 

Компоненты тензора скоростей деформаций в некоторой точке M сплошной среды определяются формулами:

 

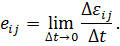
(4.15)

 

Здесь - компоненты тензора малых деформаций, произошедших в окрестности точки M за малое время . Из определения виден механический смысл компонент тензора скоростей деформаций: - это скорости относительных удлинений отрезков, в данный момент параллельных координатным осям, а 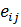при 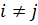равны половинам скоростей изменения углов между отрезками, в данный момент параллельными соответственно осям 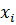и 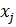. Величина первого инварианта тензора скоростей деформаций равна скорости относительного изменения объема среды в малой окрестности соответствующей точки при деформировании.

Из формул (4.12), учитывая, что предел отношения величины перемещения точки к величине промежутка времени , за который произошло это перемещение, равен скорости этой точки, выводятся следующие формулы:

 

(4.16)

 

В частности, для скорости относительного изменения объема с помощью формулы (4.13) получаем

 

.

(4.17)

 

Если среда несжимаемая, то величина объема каждой индивидуальной частицы не меняется. Таким образом, для несжимаемой среды

 

 

Вектором вихря называется вектор, определяемый формулой

 

В декартовых координатах компоненты вектора вихря вычисляются по формулам

.

 

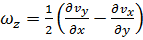В малой окрестности любой точки M сплошной среды для скоростей всех близких точек имеет место следующая формула Коши-Гельмгольца:

 

		(4.18)

где – скорость точки M (эту точку можно условно назвать центром),

- векторы базиса декартовой системы координат;

- радиус-вектор близкой точки относительно точки M;

- компоненты вектора ;

– вектор вихря.

 

Последний член в правой части этой формулы есть скорость за счет вращения частицы с мгновенной угловой скоростью . Формула (4.17) утверждает, что в малой окрестности любой точки сплошной среды движение представляет собой сумму поступательного и вращательного движения со скоростью , движения, связанного с деформированием (второй член в правой части), и вращения с угловой скоростью . Если бы частица не деформировалась, то второй член в правой части формулы (4.17) был бы равен нулю, и формула превратилась бы в известную формулу Эйлера для распределения скоростей в абсолютно твердом теле. В этом случае все материальные отрезки в частице вращались бы с мгновенной угловой скоростью . За счет деформации разные отрезки в частице поворачиваются вовсе не одинаково. Существенно также, что если среда при движении деформируется, то вектор в разных точках разный.

Если вектор вихря во всех точках равен нулю, то движение называется безвихревым. Можно доказать, что для безвихревого движения существует потенциал скорости, то есть такая функция , что

 

 

В случае, когда существует потенциал скорости, движение называется потенциальным.