

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Выясним сначала механический смысл компоненты 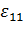 .
.
Рассмотрим малый отрезок, который до деформации был параллелен оси 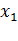 (рисунок 4.3). Обозначим через
(рисунок 4.3). Обозначим через 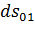 его длину до деформации,
его длину до деформации, 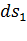 - длину после деформации. Имеем для этого отрезка
- длину после деформации. Имеем для этого отрезка
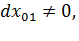
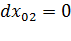 ,
, 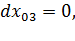
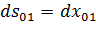 .
.
Из (4.3) получаем
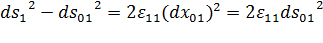
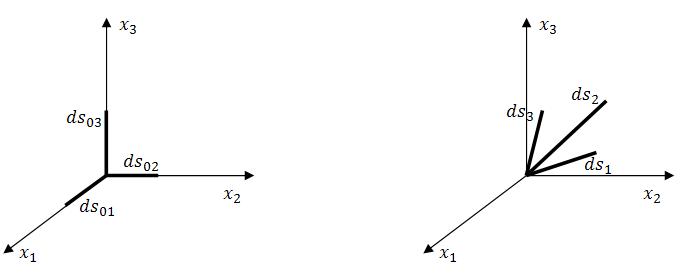
Рисунок 4.3 – Деформация малых отрезков, изначально параллельных координатным осям. Справа – отрезки до деформации, слева – отрезки после деформации
Введем понятия коэффициентов растяжения и относительного удлинения отрезков.
Коэффициент растяжения 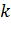 :
:
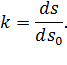
Коэффициент относительного удлинения 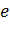 :
:
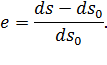
Коэффициенты растяжения и относительного удлинения рассматриваемого отрезка 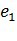 равны соответственно
равны соответственно
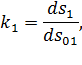
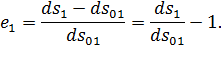
Кроме того,
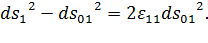
Поделив обе части последнего равенства на 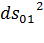 , получим
, получим
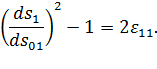
Таким образом,
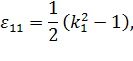
или
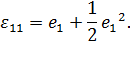
| (4.4) |
В случае малых деформаций 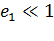 ,
, 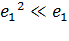 , поэтому с точностью до малых первого порядка
, поэтому с точностью до малых первого порядка
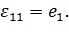
| (4.5) |
Вид соотношения (4.5) объясняет, для чего введен множитель 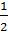 в формулах (4.2), определяющих компоненты тензора деформаций. Без этого множителя в случае малых деформаций было бы
в формулах (4.2), определяющих компоненты тензора деформаций. Без этого множителя в случае малых деформаций было бы 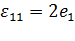 , что представляется менее естественным.
, что представляется менее естественным.
Рассматривая отрезки, лежавшие до деформации параллельно осям 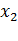 или
или 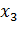 , получим формулы, аналогичные (4.4), (4.5). Итак,
, получим формулы, аналогичные (4.4), (4.5). Итак,

то есть 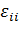 (
(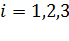 ) определяются относительными удлинениями отрезков, которые до деформации были параллельны соответственно координатным осям
) определяются относительными удлинениями отрезков, которые до деформации были параллельны соответственно координатным осям 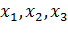 .
.
В случае малых деформаций 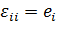 , то есть
, то есть 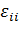 (
(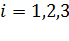 ) равны относительным удлинениям отрезков, которые до деформации были параллельны соответственно осям
) равны относительным удлинениям отрезков, которые до деформации были параллельны соответственно осям 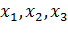 .
.
Выясним теперь механический смысл компонент тензора деформаций 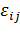 при
при 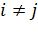 . Из определения компонент
. Из определения компонент 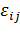 следует, что:
следует, что:
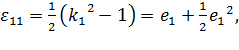 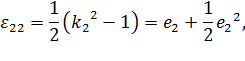
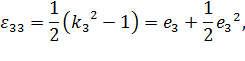
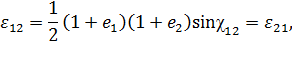
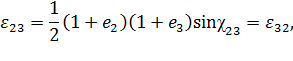
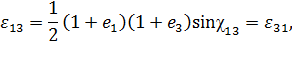
| (4.6) |
где 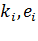 – соответственно коэффициенты растяжения и относительного удлинения отрезка, до деформации параллельного координатной оси
– соответственно коэффициенты растяжения и относительного удлинения отрезка, до деформации параллельного координатной оси 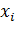 , а
, а 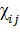 – разность между первоначально прямым углом между отрезками, которые до деформации были параллельны соответственно осям
– разность между первоначально прямым углом между отрезками, которые до деформации были параллельны соответственно осям 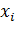 и
и 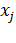 , и углом
, и углом 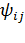 между этими отрезками после деформации (рисунок 4.4):
между этими отрезками после деформации (рисунок 4.4):
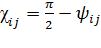 .
.
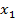
|
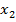
|
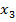
|
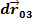
|
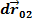
|
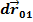
|
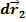
|
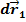
|
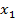
|
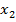
|
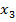
|

|
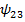
|
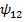
|
Рисунок 4.4 – Изменение угла между материальными отрезками при деформации
При малых деформациях 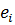 и
и 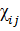 малы, поэтому с точностью до малых высшего порядка верны формулы
малы, поэтому с точностью до малых высшего порядка верны формулы
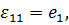 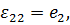 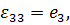 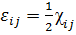 при при 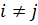 . .
| (4.7) |
Эти формулы используются в теории малых деформаций. Итак, в случае малых деформаций 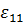 ,
, 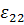 ,
, 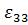 – это коэффициенты относительных удлинений отрезков, параллельных координатным осям, а
– это коэффициенты относительных удлинений отрезков, параллельных координатным осям, а 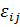 при
при 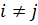 равны половинам величин изменения углов между отрезками, которые до деформации были параллельны соответственно осям
равны половинам величин изменения углов между отрезками, которые до деформации были параллельны соответственно осям 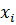 и
и 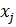 . В простейшем двумерном случае малые деформации проиллюстрировать на примере квадрата.
. В простейшем двумерном случае малые деформации проиллюстрировать на примере квадрата.
| Тело до деформации | Растяжение-сжатие | Сдвиг |
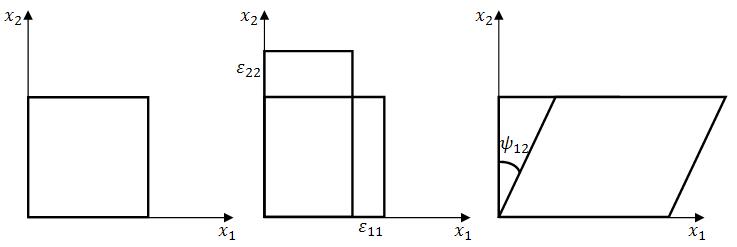
Рисунок 4.5 – Геометрическая интерпретация тензора малых деформаций
Величина относительного изменения малого объема в случае малых деформаций определяется формулой:
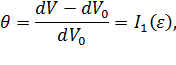
| (4.8) |
где 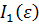 - первый инвариант тензора деформаций. В декартовых координатах
- первый инвариант тензора деформаций. В декартовых координатах
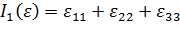 . .
| (4.9) |
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!