Поровое пространство гранулярных горных пород, а также имеющиеся в породах трещины, каверны и другие полости в естественных условиях, как правило, бывают заполнены жидкостями или газами. Эти подвижные вещества, насыщающие горные породы, находятся под давлением. В горных породах в свою очередь имеются напряжения. Любое изменение давления жидкости или газа, а также нагрузок на горные породы нарушает имеющееся в данный момент времени соотношение между давлением и напряжениями. Другими словами, между породами и насыщающими их веществами существует механическое взаимодействие.
Начнем рассмотрение механического взаимодействия горных пород и насыщающих их веществ в следующем, наиболее простом, случае. Возьмем образец пористой среды (рисунок 7.1), покрытый сверху гибкой непроницаемой оболочкой, и поместим его под пресс, создающий вертикальное давление 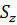 на образец. Допустим, что гидравлическим или иным способом в образце создается также горизонтальное давление
на образец. Допустим, что гидравлическим или иным способом в образце создается также горизонтальное давление 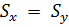 . Внутрь образца подводится по трубке жидкость, имеющая давление р. В материале образца соответственно возникают напряжения
. Внутрь образца подводится по трубке жидкость, имеющая давление р. В материале образца соответственно возникают напряжения 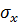 ,
, 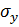 и
и 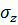 . Если, например, изменить давление жидкости
. Если, например, изменить давление жидкости 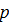 , оставив неизменными внешние нагрузки на образец
, оставив неизменными внешние нагрузки на образец 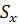 ,
,  и
и 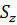 , то это должно вызвать изменение напряжений
, то это должно вызвать изменение напряжений 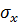 ,
, 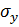 и
и 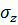 в материале образца. Возникает вопрос: каковы эти изменения в количественном отношении?
в материале образца. Возникает вопрос: каковы эти изменения в количественном отношении?
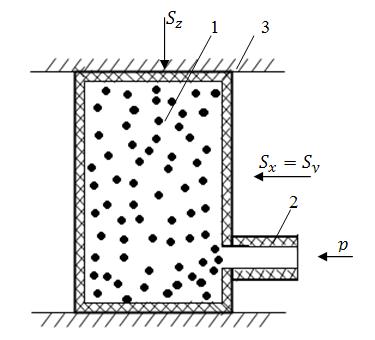
Рисунок 7.1 – Действие усилий на образец пористой горной породы:
1 – образец, 2 – трубка, 3 – гибкая непроницаемая оболочка
Прежде чем ответить на этот вопрос, разберемся в самих понятиях о напряжениях в пористом теле. Механика взаимодействия жидкостей и твердого вещества в пористом теле требует введения различных понятий о напряжениях. Если детально рассматривать деформацию самого материала пористой среды, т. е. каждого ее «зерна», то нужно пользоваться понятием истинных напряжений.
Истинные напряжения — это обычные напряжения, с которыми имеют дело при изучении деформации монолитного материала.
Если же рассматривать деформацию пористого тела в целом, т. е. принимать это тело за некоторую условно монолитную среду, то следует ввести в рассмотрение понятие об эффективном напряжении, или усилии, действующем на единичную площадку пористого тела в целом, включая как зерна, так и пустоты. Напряжения 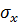 ,
, 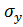 и
и 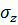 в образце пористого тела, показанного на рис. 7.2, являются эффективными напряжениями. Используем еще понятие так называемого нейтрального напряжения, создаваемого в пористом теле только внутрипоровым давлением р и приводящего к возникновению в материале пористого тела следующих истинных напряжений:
в образце пористого тела, показанного на рис. 7.2, являются эффективными напряжениями. Используем еще понятие так называемого нейтрального напряжения, создаваемого в пористом теле только внутрипоровым давлением р и приводящего к возникновению в материале пористого тела следующих истинных напряжений:
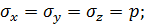
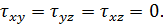
Безусловно, и эффективные напряжения и нейтральное напряжение связаны определенным образом с истинными напряжениями. Понятия об эффективном и нейтральном напряжениях были введены К. Терцаги.
Было бы, возможно, более правильным пользоваться только истинными напряжениями, однако трудность их определения в пористом теле приводит в конце концов к необходимости применения понятия эффективных напряжений, так как экспериментально их определить значительно легче.

Рисунок 7.2 – Действие усилий на зерна породы:
1 – непроницаемая оболочка, 2 – зерна породы
Вернемся теперь к поставленному выше вопросу о количественной взаимосвязи между внутрипоровым давлением  , эффективными напряжениями
, эффективными напряжениями 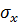 ,
, 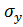 и
и 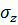 и величинами
и величинами 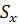 ,
,  и
и 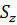 , которые назовем полными напряжениями.
, которые назовем полными напряжениями.
В связи с этим вопросом рассмотрим равновесие сил на контакте образца с прессом (рисунок 7.2, а). Пусть «зерно» породы на участке ab соприкасается с непроницаемой оболочкой и далее — с прессом, а на участках bc, de и fa (рисунок 7.2, б) смачивается жидкостью. На участках ab, cd и ef на зерно действуют осредненные напряжения 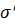 . Из равновесия усилий на участке a’b’ (рисунок 7.2, а) длиной, равной единице, получаем, считая, что смачиваемая жидкостью часть участка a’b’ равна т,
. Из равновесия усилий на участке a’b’ (рисунок 7.2, а) длиной, равной единице, получаем, считая, что смачиваемая жидкостью часть участка a’b’ равна т,
|
| 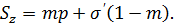
| (7.1)
|
На первый взгляд может показаться, что согласно (7.1) давление жидкости не полностью «противостоит» внешним усилиям. Однако это не так. Выше под напряжениями понимались только эффективные напряжения, а напряжение 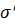 включает в себя как эффективное, так и нейтральное напряжение. В самом деле, если рассмотреть действие на зерно породы различных усилий согласно рис. 7.2, б, то можно увидеть, что сдвиговые напряжения и, следовательно, деформацию, вызывающую изменение конфигурации зерна, может создать только разность напряжений
включает в себя как эффективное, так и нейтральное напряжение. В самом деле, если рассмотреть действие на зерно породы различных усилий согласно рис. 7.2, б, то можно увидеть, что сдвиговые напряжения и, следовательно, деформацию, вызывающую изменение конфигурации зерна, может создать только разность напряжений 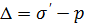 . Изменение же нейтрального напряжения не приводит к изменению эффективных напряжений. При существовании нейтрального напряжения (7.1) эффективные напряжения в пористом теле могут быть равны нулю. Эффективные напряжения вызывают изменение конфигурации скелета пористой среды; при определенном значении эффективных напряжений может произойти разрушение пористой среды. Нейтральное же напряжение вызывает лишь сжатие материала пористой среды.
. Изменение же нейтрального напряжения не приводит к изменению эффективных напряжений. При существовании нейтрального напряжения (7.1) эффективные напряжения в пористом теле могут быть равны нулю. Эффективные напряжения вызывают изменение конфигурации скелета пористой среды; при определенном значении эффективных напряжений может произойти разрушение пористой среды. Нейтральное же напряжение вызывает лишь сжатие материала пористой среды.
Вряд ли можно ожидать разрушения материала пористой среды под действием внутрипорового давления р. Поэтому с целью выделения в формуле (7.1) части, связанной с эффективным напряжением, и части, связанной с нейтральным напряжением, необходимо в (7.1) заменить 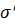 на
на 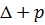 .
.
Тогда получим
|
| 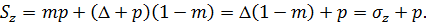
| (7.2)
|
Величина  в формуле (7.2) связана cэффективным напряжением, и виду того, что эффективное напряжение есть усилие, отнесенное ко всему участку ab, величина
в формуле (7.2) связана cэффективным напряжением, и виду того, что эффективное напряжение есть усилие, отнесенное ко всему участку ab, величина 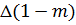 заменена на
заменена на 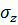 . Из формулы (7.2) теперь уже видно, что уменьшение внутрипорового давления
. Из формулы (7.2) теперь уже видно, что уменьшение внутрипорового давления 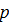 в образце на какую-то величину при неизменном полном напряжении
в образце на какую-то величину при неизменном полном напряжении 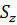 приводит к увеличению эффективного напряжения
приводит к увеличению эффективного напряжения 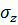 на такую же величину.
на такую же величину.
Это теоретическое положение хорошо подтверждается экспериментальными фактами. Так, разрушение покрытых непроницаемой оболочкой образцов при различных значениях внутрипорового давления  показало, что все экспериментальные точки на зависимости предельного эффективного напряжения
показало, что все экспериментальные точки на зависимости предельного эффективного напряжения 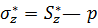 , при котором происходило разрушение образца, от предельного эффективного напряжения
, при котором происходило разрушение образца, от предельного эффективного напряжения 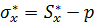 укладываются практически на одну прямую линию (рисунок 7.3), как это и следует из теории. Согласно экспериментальным данным, показанным на рисунке 7.3, получается, что коэффициент при давлении
укладываются практически на одну прямую линию (рисунок 7.3), как это и следует из теории. Согласно экспериментальным данным, показанным на рисунке 7.3, получается, что коэффициент при давлении  равен единице.
равен единице.
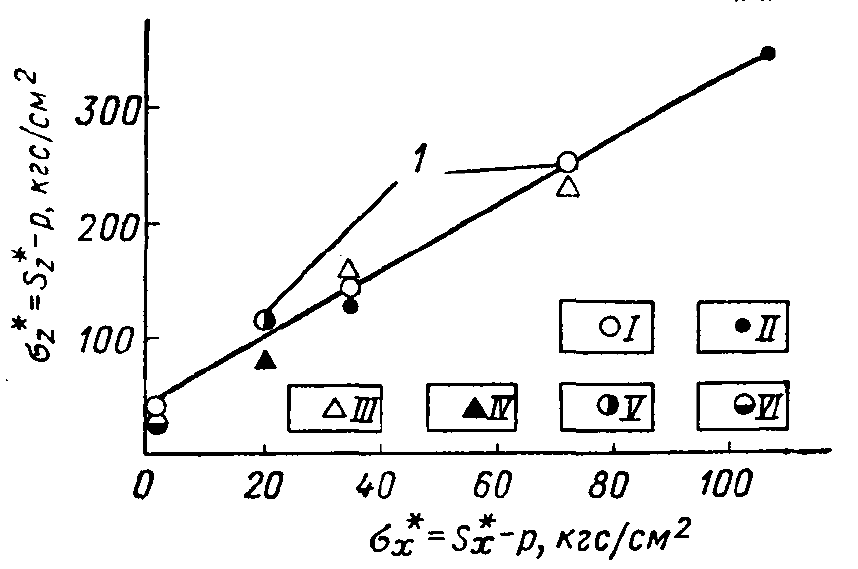
Рисунок 7.3 – Зависимость 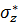 от
от 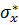 : 1 – экспериментальные точки. Случаи I-VI соответствуют давлениям
: 1 – экспериментальные точки. Случаи I-VI соответствуют давлениям  , кгс/см2: I – 0; II – 35,2; III – 70,5; IV – 106; V – 123; VI – 141
, кгс/см2: I – 0; II – 35,2; III – 70,5; IV – 106; V – 123; VI – 141
Описанные выше эксперименты относятся к разрушению пористых образцов. Если же рассматривать результаты экспериментов по сжимаемости пористых сред, то может показаться, что соотношение (7.2) не выполняется, так как коэффициент при давлении р в формуле (7.2) не равен единице (по результатам многих экспериментов он равен 0,85). Однако соотношение (7.2) справедливо и в этом случае. Дело в том, что поровый объем образца пористой среды зависит не только от эффективного напряжения, но и от нейтрального напряжения, правда, не так сильно, как от эффективного напряжения.
На рисунке 7.4 изображена в крупном масштабе пористая среда при различных значениях нейтрального напряжения 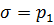 и
и  ,
, 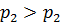 , конечно, в сильно увеличенном виде. При увеличении нейтрального напряжения от
, конечно, в сильно увеличенном виде. При увеличении нейтрального напряжения от 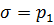 до
до  зерна пористой среды сжимаются и уменьшается поровый объем образца этой среды, как и размеры самого образца. Хотя сжимаемость материала зерен меньше сжимаемости пористой среды от эффективных напряжений, однако она существует. Изменение порового объема образца можно было бы измерить, поместив не покрытый оболочкой образец в бомбу высокого давления.
зерна пористой среды сжимаются и уменьшается поровый объем образца этой среды, как и размеры самого образца. Хотя сжимаемость материала зерен меньше сжимаемости пористой среды от эффективных напряжений, однако она существует. Изменение порового объема образца можно было бы измерить, поместив не покрытый оболочкой образец в бомбу высокого давления.
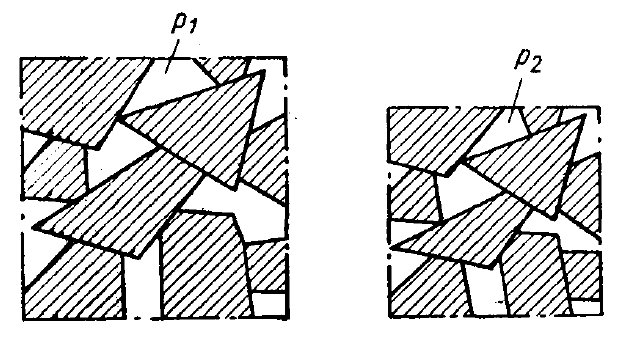
Рисунок 7.4 – Сжатие пористой среды при увеличении давления от 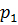 до
до 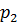
Допустим, что измеряется изменение порового объема образца пористой среды, покрытого гибкой непроницаемой оболочкой. В этом случае поровый объем образца будет зависеть главным образом от эффективных напряжений и, в известной степени, от нейтрального напряжения. Поэтому, используя радиально-симметричную cистему координат, а также считая зависимость порового объема от напряжений в первом приближении линейной, можно написать для изменения порового объема 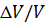 следующую формулу:
следующую формулу:
|
| 
| (7.3)
|
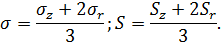
В формуле (7.3) 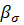 — коэффициент изменения (сжимаемости) порового объема от эффективных напряжений, а
— коэффициент изменения (сжимаемости) порового объема от эффективных напряжений, а 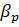 — коэффициент изменения порового объема от нейтрального напряжения. Пусть
— коэффициент изменения порового объема от нейтрального напряжения. Пусть 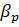 /
/ 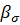 = 0,15. Тогда из (7.3) имеем
= 0,15. Тогда из (7.3) имеем 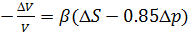 .
.
Приведенные выше рассуждения относятся к средам с сильно развитым поровым объемом. У пород кавернозного типа механическое взаимодействие твердого материала и насыщающих породу жидкостей происходит сложнее. Пусть согласно рисунку 7.5 такая порода содержит жидкость лишь в вертикально расположенных «трубочках» радиусом 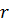 , соприкасающихся с «кровлей» по контакту ab. Эти «трубочки» расположены далеко друг от друга, так что при изменении давления жидкости в них изменение сжатия материала среды происходит практически лишь в области
, соприкасающихся с «кровлей» по контакту ab. Эти «трубочки» расположены далеко друг от друга, так что при изменении давления жидкости в них изменение сжатия материала среды происходит практически лишь в области  . Тогда изменение давления жидкости не будет вызывать в целом такого же изменения нейтрального напряжения в материале и, следовательно, приведенные выше соотношения не будут выполняться.
. Тогда изменение давления жидкости не будет вызывать в целом такого же изменения нейтрального напряжения в материале и, следовательно, приведенные выше соотношения не будут выполняться.
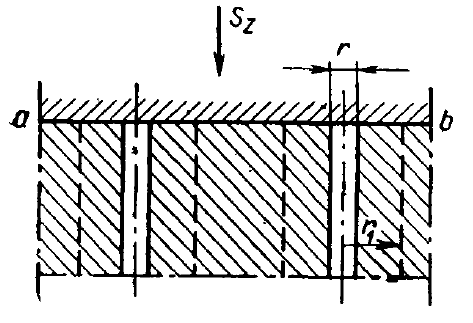
Рисунок 7.5 – Пористая среда с узкими каналами
Взаимодействие горных пород и насыщающих их жидкостей происходит, естественно, не только когда жидкость находится в покое, но и когда она движется. Если, например, имеем образец пористой среды в форме параллелепипеда (рисунок 7.5), имеющий снаружи непроницаемое покрытие, и к концу образца 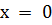 приложено давление жидкости
приложено давление жидкости 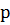 , а на другом конце образца
, а на другом конце образца 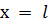 давление жидкости равно нулю, то распределение давления жидкости в порах образца будет согласно закону Дарси представлено эпюрой 3, показанной на рисунке 7.6. Давление жидкости в образце с ростом координаты
давление жидкости равно нулю, то распределение давления жидкости в порах образца будет согласно закону Дарси представлено эпюрой 3, показанной на рисунке 7.6. Давление жидкости в образце с ростом координаты 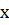 уменьшается, но поскольку давление жидкости создает усилие, которое должно восприниматься материалом пористой среды, в материале пористой среды должно с ростом координаты х увеличиваться эффективное напряжение
уменьшается, но поскольку давление жидкости создает усилие, которое должно восприниматься материалом пористой среды, в материале пористой среды должно с ростом координаты х увеличиваться эффективное напряжение 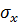 . Рассматривая равновесие сил в произвольном сечении образца, получаем, что распределение напряжения
. Рассматривая равновесие сил в произвольном сечении образца, получаем, что распределение напряжения 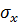 , выражается эпюрой 4, показанной на том же рис. 7.6, откуда видно, что
, выражается эпюрой 4, показанной на том же рис. 7.6, откуда видно, что
|
| 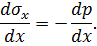
| (7.4)
|
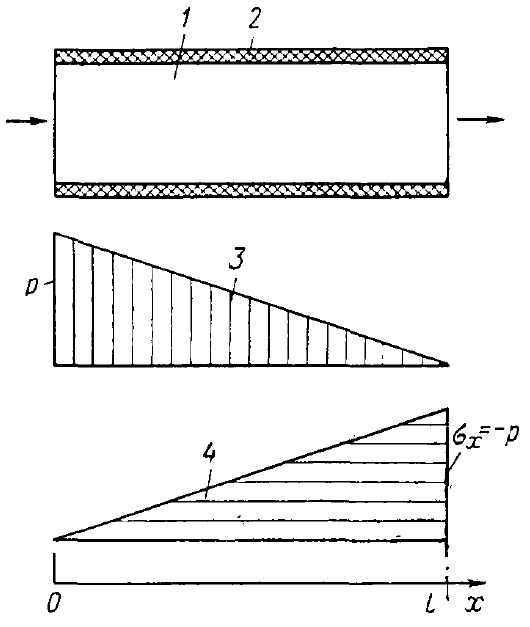
Рисунок 7.6 – Действие градиентов давления на пористую среду:
1 – образец, 2 – непроницаемое покрытие, 3 – эпюра давления, 4 – эпюра эффективного напряжения





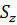 на образец. Допустим, что гидравлическим или иным способом в образце создается также горизонтальное давление
на образец. Допустим, что гидравлическим или иным способом в образце создается также горизонтальное давление 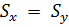 . Внутрь образца подводится по трубке жидкость, имеющая давление р. В материале образца соответственно возникают напряжения
. Внутрь образца подводится по трубке жидкость, имеющая давление р. В материале образца соответственно возникают напряжения 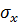 ,
, 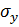 и
и 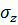 . Если, например, изменить давление жидкости
. Если, например, изменить давление жидкости 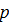 , оставив неизменными внешние нагрузки на образец
, оставив неизменными внешние нагрузки на образец 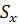 ,
,  и
и 
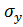 и
и 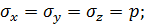
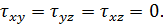

 , эффективными напряжениями
, эффективными напряжениями 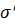 . Из равновесия усилий на участке a’b’ (рисунок 7.2, а) длиной, равной единице, получаем, считая, что смачиваемая жидкостью часть участка a’b’ равна т,
. Из равновесия усилий на участке a’b’ (рисунок 7.2, а) длиной, равной единице, получаем, считая, что смачиваемая жидкостью часть участка a’b’ равна т,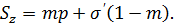
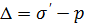 . Изменение же нейтрального напряжения не приводит к изменению эффективных напряжений. При существовании нейтрального напряжения (7.1) эффективные напряжения в пористом теле могут быть равны нулю. Эффективные напряжения вызывают изменение конфигурации скелета пористой среды; при определенном значении эффективных напряжений может произойти разрушение пористой среды. Нейтральное же напряжение вызывает лишь сжатие материала пористой среды.
. Изменение же нейтрального напряжения не приводит к изменению эффективных напряжений. При существовании нейтрального напряжения (7.1) эффективные напряжения в пористом теле могут быть равны нулю. Эффективные напряжения вызывают изменение конфигурации скелета пористой среды; при определенном значении эффективных напряжений может произойти разрушение пористой среды. Нейтральное же напряжение вызывает лишь сжатие материала пористой среды.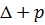 .
.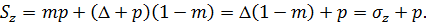
 в формуле (7.2) связана cэффективным напряжением, и виду того, что эффективное напряжение есть усилие, отнесенное ко всему участку ab, величина
в формуле (7.2) связана cэффективным напряжением, и виду того, что эффективное напряжение есть усилие, отнесенное ко всему участку ab, величина 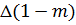 заменена на
заменена на 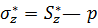 , при котором происходило разрушение образца, от предельного эффективного напряжения
, при котором происходило разрушение образца, от предельного эффективного напряжения 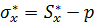 укладываются практически на одну прямую линию (рисунок 7.3), как это и следует из теории. Согласно экспериментальным данным, показанным на рисунке 7.3, получается, что коэффициент при давлении
укладываются практически на одну прямую линию (рисунок 7.3), как это и следует из теории. Согласно экспериментальным данным, показанным на рисунке 7.3, получается, что коэффициент при давлении 
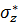 от
от 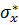 : 1 – экспериментальные точки. Случаи I-VI соответствуют давлениям
: 1 – экспериментальные точки. Случаи I-VI соответствуют давлениям 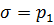 и
и  ,
, 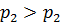 , конечно, в сильно увеличенном виде. При увеличении нейтрального напряжения от
, конечно, в сильно увеличенном виде. При увеличении нейтрального напряжения от 
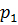 до
до 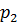
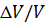 следующую формулу:
следующую формулу:
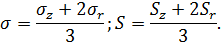
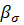 — коэффициент изменения (сжимаемости) порового объема от эффективных напряжений, а
— коэффициент изменения (сжимаемости) порового объема от эффективных напряжений, а 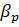 — коэффициент изменения порового объема от нейтрального напряжения. Пусть
— коэффициент изменения порового объема от нейтрального напряжения. Пусть 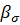 = 0,15. Тогда из (7.3) имеем
= 0,15. Тогда из (7.3) имеем 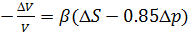 .
.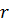 , соприкасающихся с «кровлей» по контакту ab. Эти «трубочки» расположены далеко друг от друга, так что при изменении давления жидкости в них изменение сжатия материала среды происходит практически лишь в области
, соприкасающихся с «кровлей» по контакту ab. Эти «трубочки» расположены далеко друг от друга, так что при изменении давления жидкости в них изменение сжатия материала среды происходит практически лишь в области  . Тогда изменение давления жидкости не будет вызывать в целом такого же изменения нейтрального напряжения в материале и, следовательно, приведенные выше соотношения не будут выполняться.
. Тогда изменение давления жидкости не будет вызывать в целом такого же изменения нейтрального напряжения в материале и, следовательно, приведенные выше соотношения не будут выполняться.
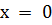 приложено давление жидкости
приложено давление жидкости 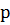 , а на другом конце образца
, а на другом конце образца 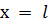 давление жидкости равно нулю, то распределение давления жидкости в порах образца будет согласно закону Дарси представлено эпюрой 3, показанной на рисунке 7.6. Давление жидкости в образце с ростом координаты
давление жидкости равно нулю, то распределение давления жидкости в порах образца будет согласно закону Дарси представлено эпюрой 3, показанной на рисунке 7.6. Давление жидкости в образце с ростом координаты 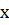 уменьшается, но поскольку давление жидкости создает усилие, которое должно восприниматься материалом пористой среды, в материале пористой среды должно с ростом координаты х увеличиваться эффективное напряжение
уменьшается, но поскольку давление жидкости создает усилие, которое должно восприниматься материалом пористой среды, в материале пористой среды должно с ростом координаты х увеличиваться эффективное напряжение