Условия оптимальности, которые дают метод динамического программирования, могут быть положены в основу создания приближенных методов решения задач определения оптимального управления.
Метод последовательных приближений.
Пусть требуется найти оптимальную программу управления системой
 ,
,  ,
,  ,
,  ,
, 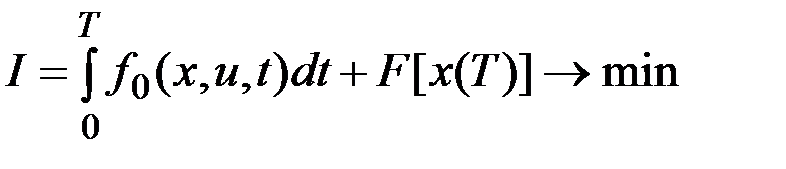 .
.
В соответствии с методом динамического программирования оптимальное управление должно удовлетворять уравнению Беллмана

при условии  . Уравнение Беллмана можно представить в следующей форме:
. Уравнение Беллмана можно представить в следующей форме:
 ,
,
 .
.
Так как при оптимальном управлении функция  обращается в нуль, то полная производная функции будущих потерь, вычисленная вдоль оптимальной траектории, равна
обращается в нуль, то полная производная функции будущих потерь, вычисленная вдоль оптимальной траектории, равна
 ,
,  .
.
Допустим, что на итерации  имеем
имеем  - некоторое допустимое управление и
- некоторое допустимое управление и  - соответствующую ему траекторию. Тогда можно вычислить функцию
- соответствующую ему траекторию. Тогда можно вычислить функцию  :
:
 ,
,
так как  при
при  .
.
Теперь построим функцию
 .
.
Минимизируя эту функцию, найдем новое  приближение для управления
приближение для управления 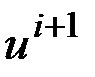 . Можно показать, что если указанное построение оказывается возможным, то последовательность управлений
. Можно показать, что если указанное построение оказывается возможным, то последовательность управлений  является минимизирующей, т.е.
является минимизирующей, т.е.  .
.
Аппроксимация функции будущих потерь. Метод параметров.
Основное рекуррентное соотношение дает формальный алгоритм численного решения. Однако аналитическое выражение для функции будущих потерь получить в общем виде не удается. Задачу можно решить приближенно, если функцию будущих потерь на каждом шаге аппроксимировать некоторой зависимостью вида
 ,
,
где  - некоторые заданные функции,
- некоторые заданные функции,  - параметры, которые определяются типом аппроксимации. Например,
- параметры, которые определяются типом аппроксимации. Например,  можно определить из условия обращения в минимум следующей квадратичной ошибки:
можно определить из условия обращения в минимум следующей квадратичной ошибки:
 .
.
Здесь под  понимаются некоторые характерные точки из допустимого множества векторов
понимаются некоторые характерные точки из допустимого множества векторов  , через
, через  обозначены значения функции будущих потерь, вычисленные для точек
обозначены значения функции будущих потерь, вычисленные для точек  согласно основному рекуррентному соотношению. Дифференцируя последнее выражение по
согласно основному рекуррентному соотношению. Дифференцируя последнее выражение по  и приравнивая производные к нулю, получаем
и приравнивая производные к нулю, получаем
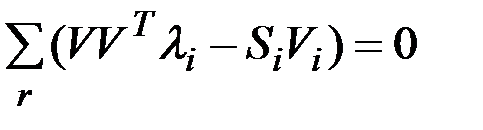 или
или  ,
,
где 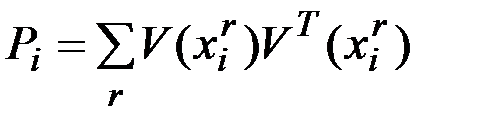 ,
, 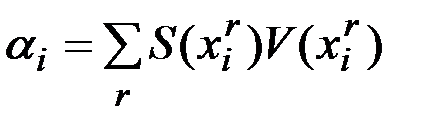 .
.
Искомый вектор параметров, обеспечивающий наилучшее приближение функции будущих потерь в смысле квадратичной ошибки  , определяется следующим образом:
, определяется следующим образом:
 .
.
При выборе структуры функций  необходимо учитывать ограничение, в силу которого должно иметь место условие
необходимо учитывать ограничение, в силу которого должно иметь место условие
 .
.
Приближенное решение уравнения Беллмана.
Метод параметров легко распространяется и на непрерывный случай, т.е. он может быть применен для приближенного решения уравнения Беллмана:
 ,
,  .
.
Представим  в виде
в виде
 ,
,
где  - заданные функции,
- заданные функции,  - функции времени, определяемые из условия
- функции времени, определяемые из условия
 ,
,
где  - множество допустимых векторов
- множество допустимых векторов  .
.
Отсюда получаем
 ,
,
 ,
,  .
.
Продифференцировав по времени, получим
 .
.
Производную  можно приближенно определить из уравнения Беллмана, тогда
можно приближенно определить из уравнения Беллмана, тогда
 .
.
Граничное условие для  получается из условия
получается из условия
 .
.





 ,
,  ,
,  ,
,  ,
, 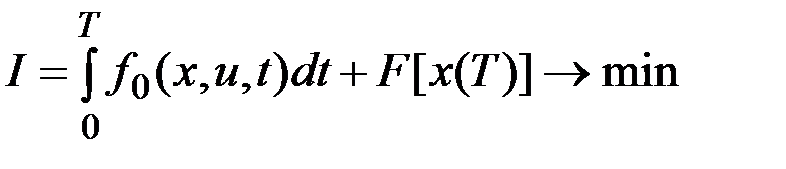 .
.
 . Уравнение Беллмана можно представить в следующей форме:
. Уравнение Беллмана можно представить в следующей форме: ,
, .
. обращается в нуль, то полная производная функции будущих потерь, вычисленная вдоль оптимальной траектории, равна
обращается в нуль, то полная производная функции будущих потерь, вычисленная вдоль оптимальной траектории, равна ,
,  .
. имеем
имеем  - некоторое допустимое управление и
- некоторое допустимое управление и  - соответствующую ему траекторию. Тогда можно вычислить функцию
- соответствующую ему траекторию. Тогда можно вычислить функцию  :
: ,
, при
при  .
. .
. приближение для управления
приближение для управления 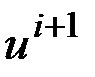 . Можно показать, что если указанное построение оказывается возможным, то последовательность управлений
. Можно показать, что если указанное построение оказывается возможным, то последовательность управлений  является минимизирующей, т.е.
является минимизирующей, т.е.  .
. ,
, - некоторые заданные функции,
- некоторые заданные функции,  - параметры, которые определяются типом аппроксимации. Например,
- параметры, которые определяются типом аппроксимации. Например,  можно определить из условия обращения в минимум следующей квадратичной ошибки:
можно определить из условия обращения в минимум следующей квадратичной ошибки: .
. понимаются некоторые характерные точки из допустимого множества векторов
понимаются некоторые характерные точки из допустимого множества векторов  , через
, через  обозначены значения функции будущих потерь, вычисленные для точек
обозначены значения функции будущих потерь, вычисленные для точек  согласно основному рекуррентному соотношению. Дифференцируя последнее выражение по
согласно основному рекуррентному соотношению. Дифференцируя последнее выражение по  и приравнивая производные к нулю, получаем
и приравнивая производные к нулю, получаем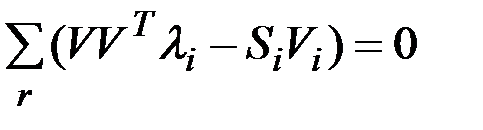 или
или  ,
,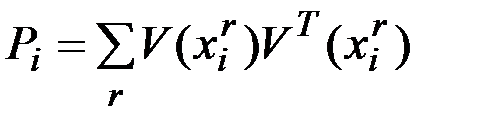 ,
, 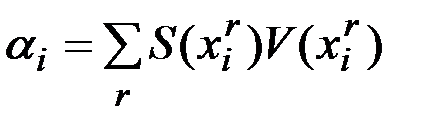 .
. , определяется следующим образом:
, определяется следующим образом: .
. необходимо учитывать ограничение, в силу которого должно иметь место условие
необходимо учитывать ограничение, в силу которого должно иметь место условие .
. ,
,  .
. в виде
в виде ,
, - заданные функции,
- заданные функции,  - функции времени, определяемые из условия
- функции времени, определяемые из условия ,
, - множество допустимых векторов
- множество допустимых векторов  .
. ,
, ,
,  .
. .
. можно приближенно определить из уравнения Беллмана, тогда
можно приближенно определить из уравнения Беллмана, тогда .
. получается из условия
получается из условия .
.

