Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения функционалов. Задачи, в которых требуется исследовать функционал на максимум или минимум, называются вариационными [1].
Определение. Переменная величина  называется функционалом от функции
называется функционалом от функции  , если каждой функции
, если каждой функции  из некоторого класса функций
из некоторого класса функций  соответствует определенное значение
соответствует определенное значение  .
.
Рис.2.1. Длина дуги кривой – функционал от функции 
|
Считается, что функционал задан, если каждой функции или кривой поставлено в соответствие некоторое число

.
Например, функционалом является длина  дуги кривой, соединяющей две точки
дуги кривой, соединяющей две точки  и
и  (рис.2.1). Величина
(рис.2.1). Величина  может быть вычислена, если задано уравнение кривой
может быть вычислена, если задано уравнение кривой  :
:
 .
.
Запишем общее выражение для функционала в виде
 , (2.1)
, (2.1)
где  - одна из возможных непрерывно дифференцируемых функций на отрезке
- одна из возможных непрерывно дифференцируемых функций на отрезке  .
.
Существует связь задачи вариационного исчисления с задачей отыскания экстремума функции многих переменных: если разбить отрезок  на
на  частей и рассмотреть ломаную линию вместо кривой
частей и рассмотреть ломаную линию вместо кривой  , а функционал
, а функционал  заменить суммой
заменить суммой
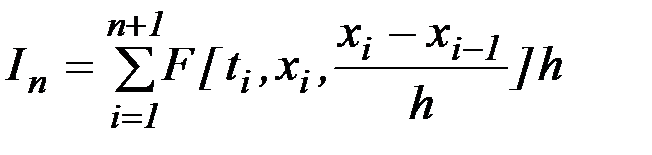 , (2.2)
, (2.2)
где  , то вариационная задача трансформируется в задачу о нахождении экстремума функции
, то вариационная задача трансформируется в задачу о нахождении экстремума функции  переменных и может быть решена классическими методами. Такой подход впервые был предложен Л. Эйлером.
переменных и может быть решена классическими методами. Такой подход впервые был предложен Л. Эйлером.
Определение. Пространство, элементами которого, являются функции, называется функциональным.
Функциональные пространства выбираются в соответствии с характером вариационной задачи. Например, при рассмотрении функционалов вида

функция  должна иметь непрерывную первую производную; при рассмотрении функционалов вида
должна иметь непрерывную первую производную; при рассмотрении функционалов вида

функция  должна иметь непрерывные первую и вторую производные и т.д.
должна иметь непрерывные первую и вторую производные и т.д.
Назовем линейным пространством 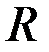 совокупность элементов
совокупность элементов  , для которых определены операции сложения и умножения на число и выполняются следующие аксиомы:
, для которых определены операции сложения и умножения на число и выполняются следующие аксиомы:
1. коммутативности сложения  ,
,
2. ассоциативности сложения  ,
,
3. существования нулевого элемента  ,
,
4. существования противоположного элемента
 :
:  ,
,
5. существования единичного элемента 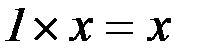 ,
,
6. ассоциативности умножения  , где
, где  и
и  - числа,
- числа,
7. дистрибутивности по сложению  ,
,
8. дистрибутивности по умножению  .
.
Линейное пространство называется нормированным, если каждому элементу 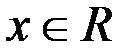 поставлено в соответствие неотрицательное число
поставлено в соответствие неотрицательное число 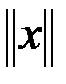 (норма этого элемента) такое, что выполняются свойства:
(норма этого элемента) такое, что выполняются свойства:
1.  только при
только при  ,
,
2.  ,
,
3.  .
.
Введем понятие близости элементов, используя понятие нормы их разности, которое аналогично понятию расстояния между точками в эвклидовом пространстве.
Рис.2.2. Сильная окрестность кривой 
|
Рассмотрим пространство

, состоящее из непрерывных функций, определенных на отрезке

. Норму функции определим как

. Расстояние между точками пространства

будет

. Функции

и

близки в смысле близости нулевого порядка, если модуль разности

не превышает некоторой наперед заданной малой положительной величины

:
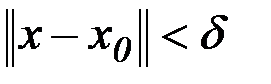
. Такая окрестность называется сильной (рис. 2.2).
Рассмотрим пространство  , состоящее из непрерывных функций, определенных на отрезке
, состоящее из непрерывных функций, определенных на отрезке  и имеющих непрерывные первые производные. Очевидно,
и имеющих непрерывные первые производные. Очевидно,  . Функции
. Функции  и
и  близки в смысле близости первого порядка, если
близки в смысле близости первого порядка, если 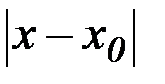 и
и 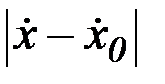 , а также
, а также  не превышают некоторой наперед заданной малой положительной величины
не превышают некоторой наперед заданной малой положительной величины  :
:  ,
,  ,
,  . Такая окрестность называется слабой (рис. 2.3).
. Такая окрестность называется слабой (рис. 2.3).
Рис.2.3. Слабая окрестность кривой 
|
Соответственно вводится понятие близости k-ого порядка, соответствующее функциональному пространству

.
Определение. Функционал  называется непрерывным при
называется непрерывным при  , если для любого положительного
, если для любого положительного  можно подобрать
можно подобрать  , что
, что  при
при  , где
, где  - норма, определенная в смысле близости функций
- норма, определенная в смысле близости функций  и
и  k-го порядка
k-го порядка
Определение. Линейным называется функционал  , удовлетворяющий следующим условиям.
, удовлетворяющий следующим условиям.
1. Функционал  является непрерывным,
является непрерывным,
2.  ,
,
3.  .
.
Общий вид линейного функционала
 . (2.3)
. (2.3)
2.2. Вариация функционала.





 называется функционалом от функции
называется функционалом от функции  , если каждой функции
, если каждой функции  из некоторого класса функций
из некоторого класса функций  соответствует определенное значение
соответствует определенное значение  .
.
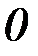

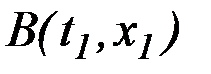
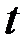

 .
.
 дуги кривой, соединяющей две точки
дуги кривой, соединяющей две точки  и
и  (рис.2.1). Величина
(рис.2.1). Величина 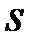 может быть вычислена, если задано уравнение кривой
может быть вычислена, если задано уравнение кривой  :
: .
. , (2.1)
, (2.1) - одна из возможных непрерывно дифференцируемых функций на отрезке
- одна из возможных непрерывно дифференцируемых функций на отрезке  .
. на
на  частей и рассмотреть ломаную линию вместо кривой
частей и рассмотреть ломаную линию вместо кривой  , а функционал
, а функционал  заменить суммой
заменить суммой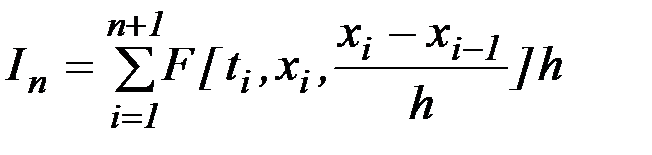 , (2.2)
, (2.2) , то вариационная задача трансформируется в задачу о нахождении экстремума функции
, то вариационная задача трансформируется в задачу о нахождении экстремума функции  переменных и может быть решена классическими методами. Такой подход впервые был предложен Л. Эйлером.
переменных и может быть решена классическими методами. Такой подход впервые был предложен Л. Эйлером. должна иметь непрерывную первую производную; при рассмотрении функционалов вида
должна иметь непрерывную первую производную; при рассмотрении функционалов вида
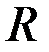 совокупность элементов
совокупность элементов  , для которых определены операции сложения и умножения на число и выполняются следующие аксиомы:
, для которых определены операции сложения и умножения на число и выполняются следующие аксиомы: ,
, ,
, ,
, :
:  ,
,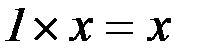 ,
, , где
, где  и
и  - числа,
- числа, ,
, .
.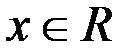 поставлено в соответствие неотрицательное число
поставлено в соответствие неотрицательное число 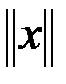 (норма этого элемента) такое, что выполняются свойства:
(норма этого элемента) такое, что выполняются свойства: только при
только при  ,
, ,
, .
.







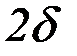
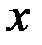

 , состоящее из непрерывных функций, определенных на отрезке
, состоящее из непрерывных функций, определенных на отрезке  . Норму функции определим как
. Норму функции определим как  . Расстояние между точками пространства
. Расстояние между точками пространства  будет
будет  . Функции
. Функции  и
и  близки в смысле близости нулевого порядка, если модуль разности
близки в смысле близости нулевого порядка, если модуль разности  не превышает некоторой наперед заданной малой положительной величины
не превышает некоторой наперед заданной малой положительной величины  :
: 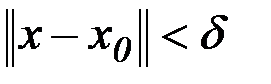 . Такая окрестность называется сильной (рис. 2.2).
. Такая окрестность называется сильной (рис. 2.2).
 , состоящее из непрерывных функций, определенных на отрезке
, состоящее из непрерывных функций, определенных на отрезке  . Функции
. Функции 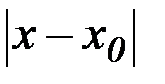 и
и 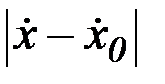 , а также
, а также  не превышают некоторой наперед заданной малой положительной величины
не превышают некоторой наперед заданной малой положительной величины  ,
,  ,
,  . Такая окрестность называется слабой (рис. 2.3).
. Такая окрестность называется слабой (рис. 2.3).

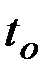




 .
.
 называется непрерывным при
называется непрерывным при  , если для любого положительного
, если для любого положительного  можно подобрать
можно подобрать  , что
, что  при
при  , где
, где  - норма, определенная в смысле близости функций
- норма, определенная в смысле близости функций  и
и  k-го порядка
k-го порядка , удовлетворяющий следующим условиям.
, удовлетворяющий следующим условиям. является непрерывным,
является непрерывным, ,
, .
. . (2.3)
. (2.3)


