Реализация метода последовательной линеаризации осуществляется с использованием конечномерной аппроксимации, которая позволяет процесс улучшения управления свести к последовательному решению стандартных задач линейного программирования. Хорошо разработанный и широко применяемый математический аппарат линейного программирования позволяет эффективно решать задачи с ограничениями. Рассмотрим способы редукции непрерывной задачи (6.6) - (6.8) к последовательности решений задач линейного программирования конечной размерности.
При выполнении итерации улучшения управления методом последовательной линеаризации исходная задача преобразуется в конечномерную вследствие замены дифференциальных уравнений движения (6.1) конечно-разностными при их численном интегрировании. В процессе численного интегрирования на отрезке времени  , относящемся к исследуемому участку траектории, располагаются точки
, относящемся к исследуемому участку траектории, располагаются точки 
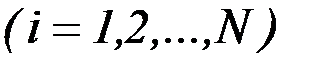 - узлы, которым соответствует вся необходимая информация для решения линейного приближения задачи (6.6) - (6.8).
- узлы, которым соответствует вся необходимая информация для решения линейного приближения задачи (6.6) - (6.8).
После расположения узлов  вычисляются значения в узловых точках фазовых координат
вычисляются значения в узловых точках фазовых координат  , сопряженных переменных
, сопряженных переменных 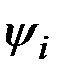 и функциональных производных
и функциональных производных 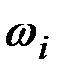 , а также фиксируются значения управляющих зависимостей
, а также фиксируются значения управляющих зависимостей  . В дальнейшем эти величины используются при аппроксимации зависимостей от времени фазовых координат, сопряженных переменных, функциональных производных и управляющих воздействий. Таким образом, непрерывная задача (6.6) - (6.8) преобразуется в конечномерную, пригодную для численного решения.
. В дальнейшем эти величины используются при аппроксимации зависимостей от времени фазовых координат, сопряженных переменных, функциональных производных и управляющих воздействий. Таким образом, непрерывная задача (6.6) - (6.8) преобразуется в конечномерную, пригодную для численного решения.
В результате конечномерной аппроксимации на каждой итерации улучшения управления условия (6.6) - (6.8) представляются в форме стандартной задачи линейного программирования. Для этого все используемые зависимости, представленные конечным набором значений в узлах, аппроксимируются по определенному правилу.
Процедура расчета итерации улучшения опорного управления при кусочно-линейной аппроксимации зависимостей формируется следующим образом.
Управление 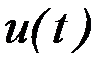 представляет собой вектор-функцию размерности
представляет собой вектор-функцию размерности  . Пусть каждый компонент
. Пусть каждый компонент 
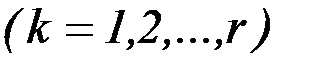 опорного управления
опорного управления 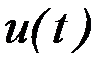 аппроксимирован непрерывной кусочно-линейной функцией со значениями
аппроксимирован непрерывной кусочно-линейной функцией со значениями  в узловых точках
в узловых точках 
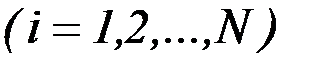 .В дальнейшем индекс «
.В дальнейшем индекс « » не будет указываться, и под управлением
» не будет указываться, и под управлением 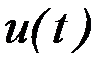 будем понимать в зависимости от контекста или вектор-функцию размерности
будем понимать в зависимости от контекста или вектор-функцию размерности 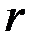 или ее
или ее 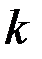 -ый компонент.
-ый компонент.
Тогда 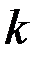 -й компонент управления
-й компонент управления 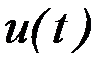 , представленный в классе кусочно-линейных функций, в каждый момент времени
, представленный в классе кусочно-линейных функций, в каждый момент времени  может быть рассчитан по формуле:
может быть рассчитан по формуле:
 ,
, 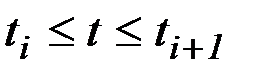
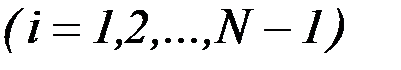 .
.
Возмущение  каждого
каждого  -того компонента управления
-того компонента управления 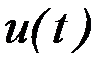 , представленное в том же классе функций, имеет вид:
, представленное в том же классе функций, имеет вид:
 ,
, 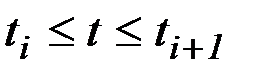
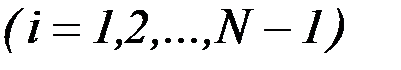 ,
,
где  и
и 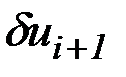 - постоянные величины, представляющие собой вариации непрерывного кусочно-линейного управления в узловых точках.
- постоянные величины, представляющие собой вариации непрерывного кусочно-линейного управления в узловых точках.
При этих допущениях условия (6.6) - (6.8) приводятся к следующей задаче линейного программирования относительно неизвестных 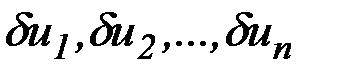 :
:
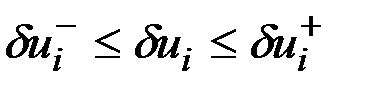
 , (6.16)
, (6.16)

 , (6.17)
, (6.17)
 , (6.18)
, (6.18)
где 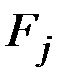 - значения функционалов, вычисленные для опорного закона движения
- значения функционалов, вычисленные для опорного закона движения  ;
; 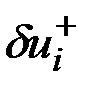 ,
,  - малые заданные величины.
- малые заданные величины.
Коэффициенты 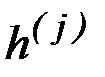 вычисляются по интегральным соотношениям:
вычисляются по интегральным соотношениям:
 ,
,
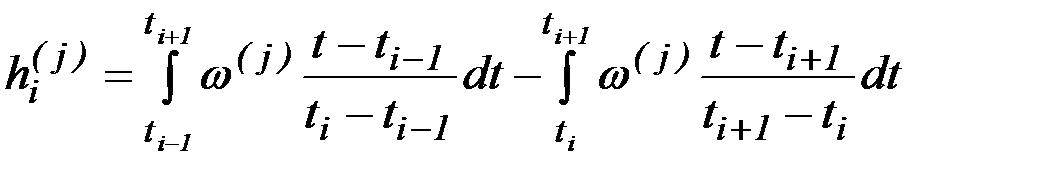
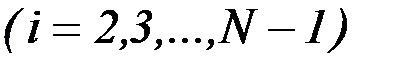 ,
,

 . (6.19)
. (6.19)
Если известны значения функциональных производных  в узлах
в узлах 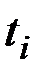
 , то, используя кусочно-линейную аппроксимацию зависимостей
, то, используя кусочно-линейную аппроксимацию зависимостей 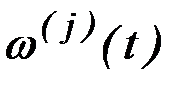 , получим следующие формулы для вычисления коэффициентов
, получим следующие формулы для вычисления коэффициентов 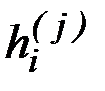 :
:
 ,
,

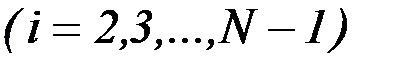

 . (6.20)
. (6.20)
В некоторых случаях при аппроксимации задачи более подходящими могут оказаться кусочно-постоянные аппроксимирующие зависимости, упрощающие вычислительную процедуру решения по сравнению с использованием кусочно-линейных зависимостей.
Наиболее просто задача расположения узлов решается, если узлы расположить равномерно по времени на отрезке  . При изменении эффективности управления наибольшая концентрация узлов необходима в местах наиболее интенсивного изменения и наибольшей эффективности управления.
. При изменении эффективности управления наибольшая концентрация узлов необходима в местах наиболее интенсивного изменения и наибольшей эффективности управления.
Метод плавающих узлов обеспечивает рациональное распределение узлов аппроксимации и учет изменения длины отрезка 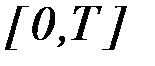 в процессе улучшения управления.
в процессе улучшения управления.
Для рассмотрения метода плавающих узлов удобно использовать функцию Гамильтона, которая для функционалов (6.9) и (6.15) имеет вид:
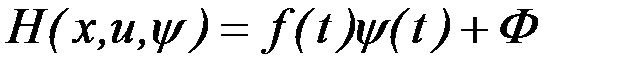 .
.
Для функционалов (6.10) гамильтониан записывается в виде:
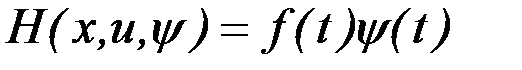 .
.
Вектор-функция  определяется из решения сопряженной системы вида:
определяется из решения сопряженной системы вида:
 . (6.21)
. (6.21)
Для функционалов вида (6.9)  , для функционалов вида (2.10)
, для функционалов вида (2.10)  , а для функционалов вида (6.10)
, а для функционалов вида (6.10)  , причем
, причем 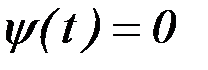 при
при 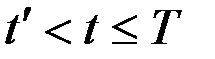 .
.
Можно показать, что условия (6.6) - (6.8) с помощью функции Гамильтона могут быть преобразованы и записаны в следующем виде:
 при всех
при всех  , (6.22)
, (6.22)
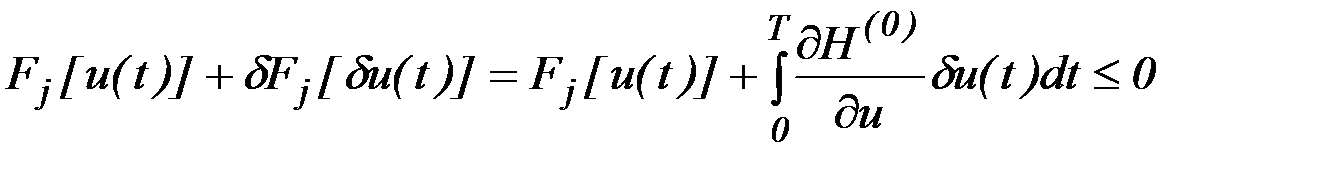 , (6.23)
, (6.23)
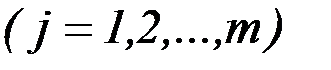 ,
,
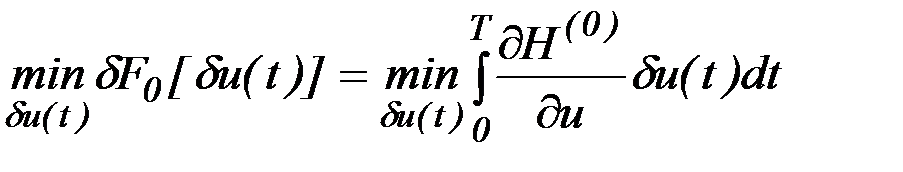 . (6.24)
. (6.24)
Для функционалов вида (6.11) и (6.12) гамильтонианы записаны быть не могут, поэтому при численном решении эти функционалы заменяются на функционалы других видов в соответствии с выбранной процедурой.
Значения функций  , соответствующих функциональным производным
, соответствующих функциональным производным 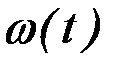 , определяются по формулам:
, определяются по формулам:
 , (6.25)
, (6.25)
для функционалов вида (6.10) 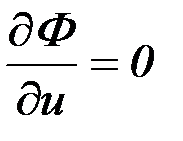 . Таким образом, для определения зависимости
. Таким образом, для определения зависимости  необходимо проинтегрировать слева направо систему (1.9) и справа налево систему (6.21).
необходимо проинтегрировать слева направо систему (1.9) и справа налево систему (6.21).
Метод плавающих узлов основан на замене независимой переменной путем отображения отрезка времени  в отрезок
в отрезок  . Для этого вводится функция
. Для этого вводится функция 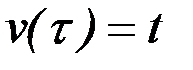 ,
,  ,
,  ,
,  , которая должна удовлетворять условию монотонности
, которая должна удовлетворять условию монотонности 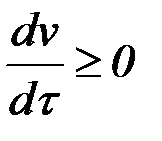 , исключающему обратный ход времени. Функция
, исключающему обратный ход времени. Функция 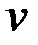 является дополнительным управлением, связанным с расположением узлов аппроксимации.
является дополнительным управлением, связанным с расположением узлов аппроксимации.
Система уравнений (6.1), функционалы (6.9), (6.10) и (6.15) после замены переменной приобретают вид:
 ,
,
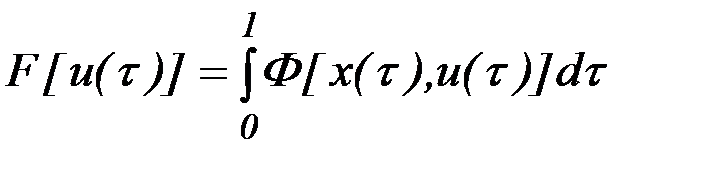 ,
,
 ,
,
 ,
,
где  - заданная точка на
- заданная точка на  .
.
Вариации функционалов после замены независимой переменной зависят от малых локальных вариаций  управления
управления  и
и  функции замены времени
функции замены времени  следующим образом:
следующим образом:
 .
.
Выражение для вариации функциональной производной приводится к виду:
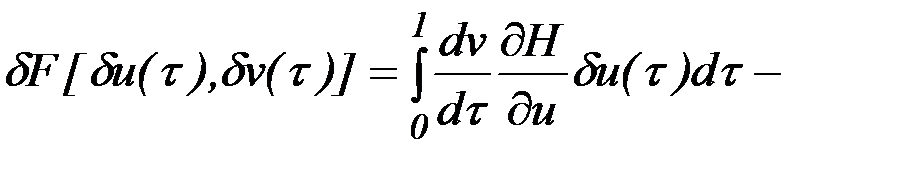
 .
.
Последнее соотношение позволяет преобразовать условия (6.22) - (6.24) к виду:
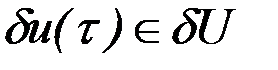 ,
,  при всех
при всех 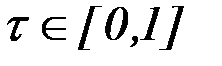 , (6.26)
, (6.26)

 , (6.27)
, (6.27)
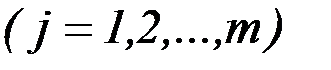 ,
,
 ,
,
(6.28)
где  - малая окрестность функции
- малая окрестность функции  .
.
При численном решении управление  и функция
и функция  задаются набором значений в узловых точках на отрезке
задаются набором значений в узловых точках на отрезке  . Условия (2.22) - (2.24) приводятся к задаче линейного программирования относительно неизвестных
. Условия (2.22) - (2.24) приводятся к задаче линейного программирования относительно неизвестных  и
и  :
:
 ,
, 
 , (6.29)
, (6.29)
 ,
,  , (6.30)
, (6.30)
 , (6.31)
, (6.31)
где  ,
,  ,
,  ,
,  - малые заданные величины;
- малые заданные величины;  ,
,  - коэффициенты, определяемые по интегральным зависимостям, например:
- коэффициенты, определяемые по интегральным зависимостям, например:
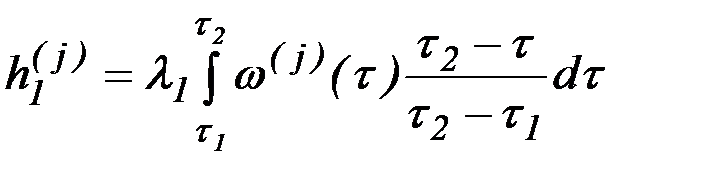 ,
,
 ,
,
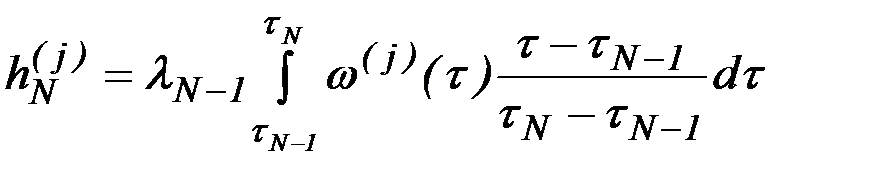 ,
,
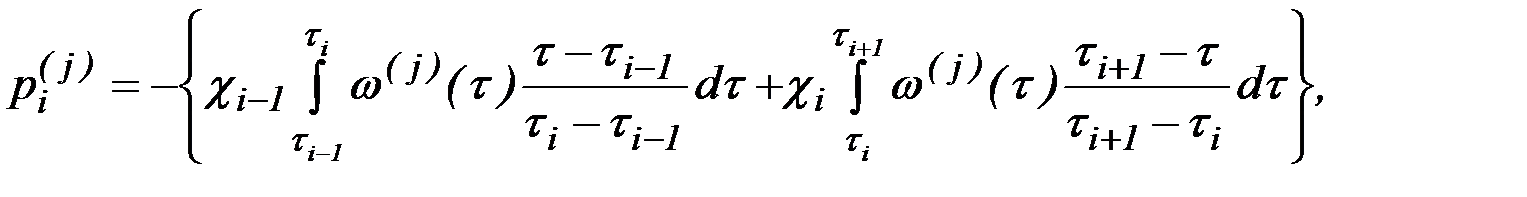
 ,
,
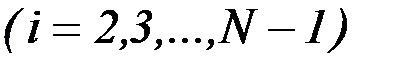 ,
,  . (6.32)
. (6.32)
Поиск управления 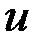 , функции
, функции  , вариаций
, вариаций  и
и 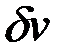 , а также представление производных
, а также представление производных  в классе кусочно-линейных функций позволяет получить конечные соотношения для производных
в классе кусочно-линейных функций позволяет получить конечные соотношения для производных 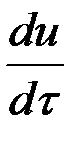 ,
,  и коэффициентов
и коэффициентов 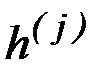 и
и  .
.
Кусочно-линейные зависимости управления  , функции
, функции 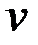 , вариаций
, вариаций  и
и  и производных
и производных 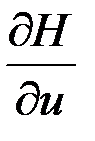 имеют вид:
имеют вид:
 ,
,
 ,
,
 ,
,
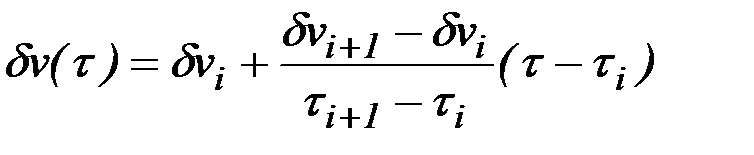 ,
,

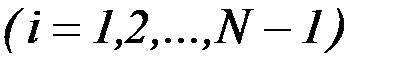 ,
,
где  ,
,  ,
,  ,
, 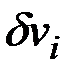 ,
,  - значения величин в узловых точках
- значения величин в узловых точках  .
.
Значения производных  и
и  в узловых точках вычисляются по формулам:
в узловых точках вычисляются по формулам:
 ,
,
 ,
, 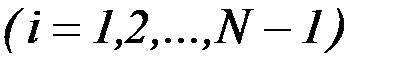
Выполнение условия  обеспечивается при
обеспечивается при

 ,
,

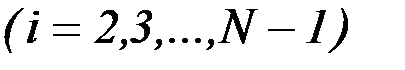 .
.
Возможность совпадения двух соседних узловых точек позволяет формировать не только непрерывное, но и разрывное кусочно-линейное управление. Малость допустимой окрестности  обеспечивается заданием ограничений
обеспечивается заданием ограничений  ,
,  где
где 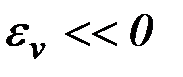 .
.
Коэффициенты  и
и  вычисляются по формулам:
вычисляются по формулам:
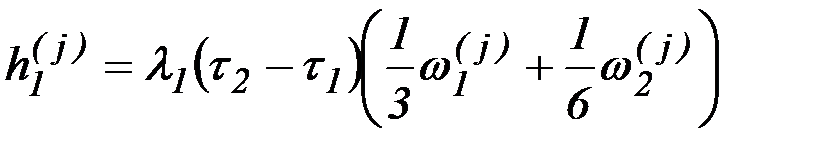 ,
,
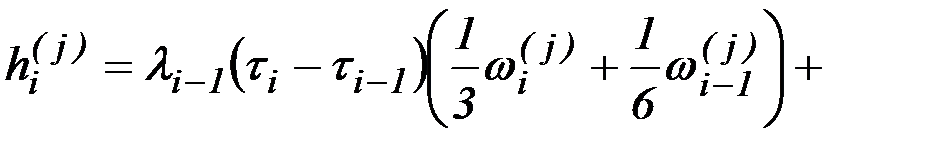
 ,
,
 ,
,

 ,
,
 ,
,
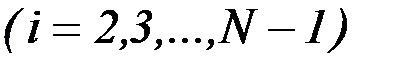
 . (6.33)
. (6.33)
Использование метода плавающих узлов вместо других способов конечномерной аппроксимации задачи совместно с методом последовательной линеаризации приводит к повышению размерности задачи линейного программирования. Если размерность матрицы коэффициентов  (6.20) без использования метода плавающих узлов равна
(6.20) без использования метода плавающих узлов равна 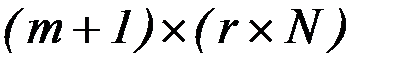 , где
, где  - число функционалов задачи,
- число функционалов задачи,  - размерность вектора управлений,
- размерность вектора управлений, 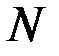 - число узловых точек аппроксимации, то при использовании метода плавающих узлов общая размерность матриц
- число узловых точек аппроксимации, то при использовании метода плавающих узлов общая размерность матриц 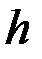 и
и  (6.33) увеличивается до
(6.33) увеличивается до  .
.



 , относящемся к исследуемому участку траектории, располагаются точки
, относящемся к исследуемому участку траектории, располагаются точки 
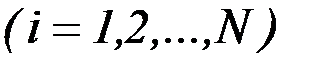 - узлы, которым соответствует вся необходимая информация для решения линейного приближения задачи (6.6) - (6.8).
- узлы, которым соответствует вся необходимая информация для решения линейного приближения задачи (6.6) - (6.8). , сопряженных переменных
, сопряженных переменных 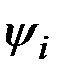 и функциональных производных
и функциональных производных 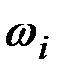 , а также фиксируются значения управляющих зависимостей
, а также фиксируются значения управляющих зависимостей  . В дальнейшем эти величины используются при аппроксимации зависимостей от времени фазовых координат, сопряженных переменных, функциональных производных и управляющих воздействий. Таким образом, непрерывная задача (6.6) - (6.8) преобразуется в конечномерную, пригодную для численного решения.
. В дальнейшем эти величины используются при аппроксимации зависимостей от времени фазовых координат, сопряженных переменных, функциональных производных и управляющих воздействий. Таким образом, непрерывная задача (6.6) - (6.8) преобразуется в конечномерную, пригодную для численного решения.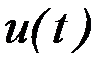 представляет собой вектор-функцию размерности
представляет собой вектор-функцию размерности  . Пусть каждый компонент
. Пусть каждый компонент 
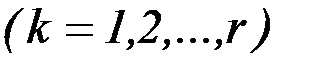 опорного управления
опорного управления  в узловых точках
в узловых точках  » не будет указываться, и под управлением
» не будет указываться, и под управлением 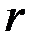 или ее
или ее 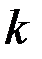 -ый компонент.
-ый компонент.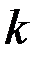 -й компонент управления
-й компонент управления  может быть рассчитан по формуле:
может быть рассчитан по формуле: ,
, 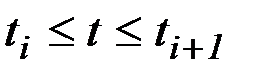
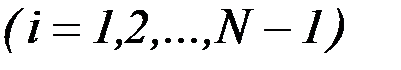 .
. каждого
каждого  -того компонента управления
-того компонента управления  ,
,  и
и 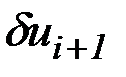 - постоянные величины, представляющие собой вариации непрерывного кусочно-линейного управления в узловых точках.
- постоянные величины, представляющие собой вариации непрерывного кусочно-линейного управления в узловых точках.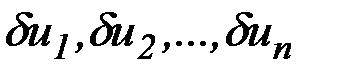 :
: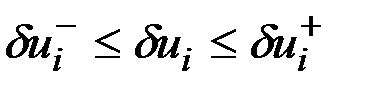
 , (6.16)
, (6.16)
 , (6.17)
, (6.17) , (6.18)
, (6.18)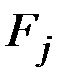 - значения функционалов, вычисленные для опорного закона движения
- значения функционалов, вычисленные для опорного закона движения  ;
; 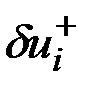 ,
,  - малые заданные величины.
- малые заданные величины.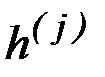 вычисляются по интегральным соотношениям:
вычисляются по интегральным соотношениям: ,
,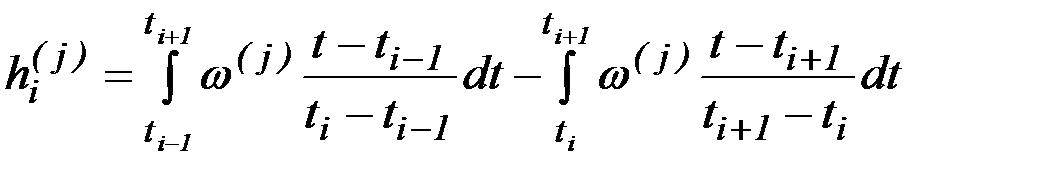
 ,
,
 . (6.19)
. (6.19) в узлах
в узлах 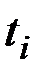
 , то, используя кусочно-линейную аппроксимацию зависимостей
, то, используя кусочно-линейную аппроксимацию зависимостей 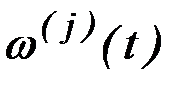 , получим следующие формулы для вычисления коэффициентов
, получим следующие формулы для вычисления коэффициентов 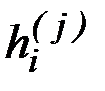 :
: ,
,

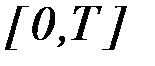 в процессе улучшения управления.
в процессе улучшения управления.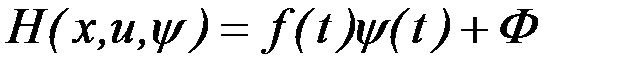 .
.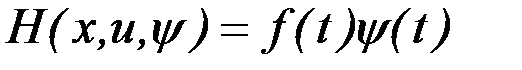 .
. определяется из решения сопряженной системы вида:
определяется из решения сопряженной системы вида: . (6.21)
. (6.21) , для функционалов вида (2.10)
, для функционалов вида (2.10)  , а для функционалов вида (6.10)
, а для функционалов вида (6.10)  , причем
, причем 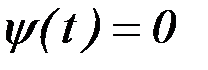 при
при 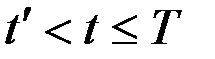 .
. при всех
при всех  , (6.22)
, (6.22)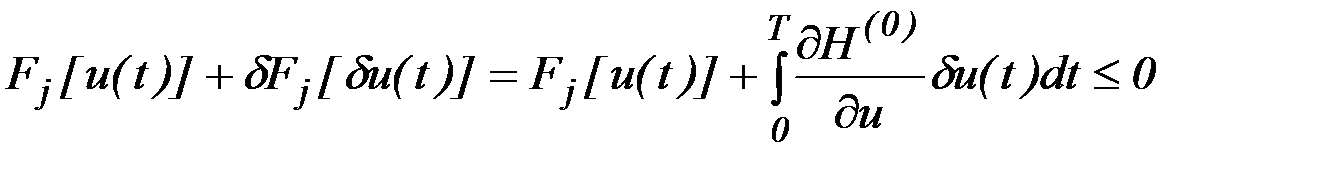 , (6.23)
, (6.23)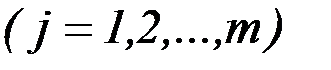 ,
,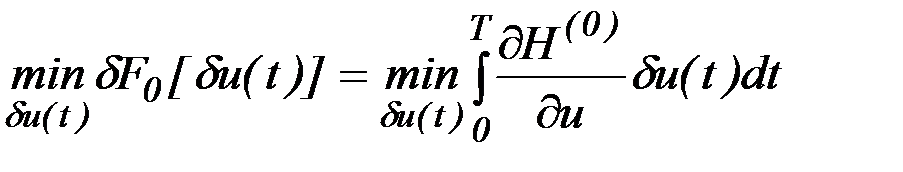 . (6.24)
. (6.24) , соответствующих функциональным производным
, соответствующих функциональным производным  , определяются по формулам:
, определяются по формулам: , (6.25)
, (6.25)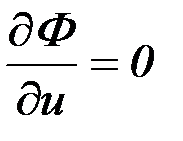 . Таким образом, для определения зависимости
. Таким образом, для определения зависимости  . Для этого вводится функция
. Для этого вводится функция 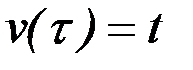 ,
,  ,
,  ,
,  , которая должна удовлетворять условию монотонности
, которая должна удовлетворять условию монотонности 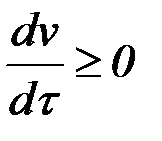 , исключающему обратный ход времени. Функция
, исключающему обратный ход времени. Функция 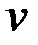 является дополнительным управлением, связанным с расположением узлов аппроксимации.
является дополнительным управлением, связанным с расположением узлов аппроксимации. ,
,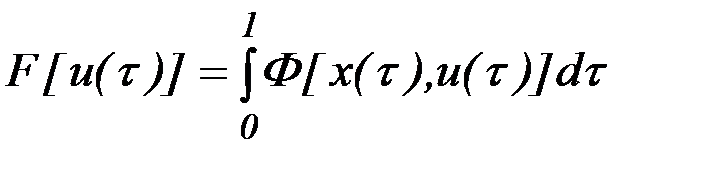 ,
, ,
, ,
, - заданная точка на
- заданная точка на  .
. управления
управления  и
и  функции замены времени
функции замены времени  следующим образом:
следующим образом: .
.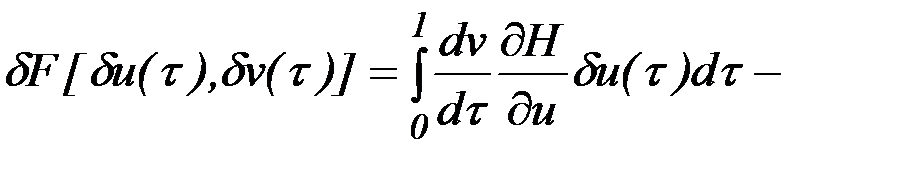
 .
. ,
,  при всех
при всех  , (6.26)
, (6.26)
 , (6.27)
, (6.27) ,
, - малая окрестность функции
- малая окрестность функции  .
. и функция
и функция  задаются набором значений в узловых точках на отрезке
задаются набором значений в узловых точках на отрезке  . Условия (2.22) - (2.24) приводятся к задаче линейного программирования относительно неизвестных
. Условия (2.22) - (2.24) приводятся к задаче линейного программирования относительно неизвестных  и
и  :
: ,
, 
 , (6.29)
, (6.29) ,
,  , (6.30)
, (6.30) , (6.31)
, (6.31) ,
,  ,
,  ,
,  - малые заданные величины;
- малые заданные величины;  ,
,  - коэффициенты, определяемые по интегральным зависимостям, например:
- коэффициенты, определяемые по интегральным зависимостям, например: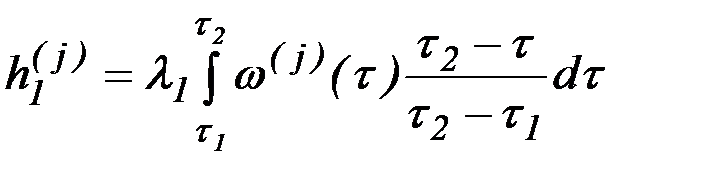 ,
, ,
,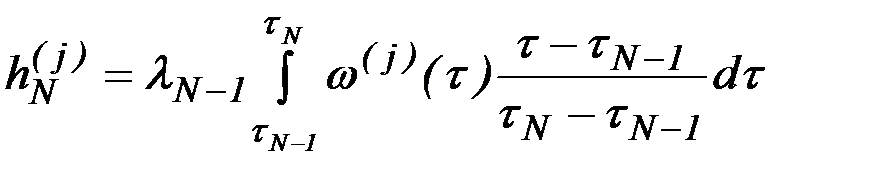 ,
,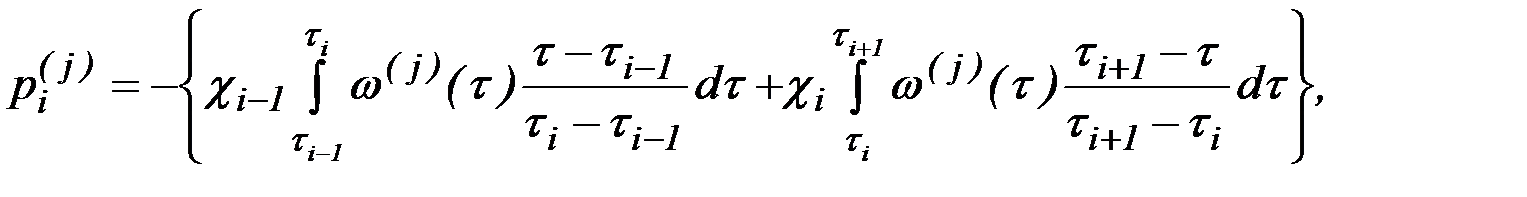
 ,
, , функции
, функции  , вариаций
, вариаций  и
и 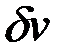 , а также представление производных
, а также представление производных  в классе кусочно-линейных функций позволяет получить конечные соотношения для производных
в классе кусочно-линейных функций позволяет получить конечные соотношения для производных 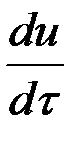 ,
,  и коэффициентов
и коэффициентов 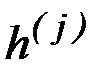 и
и  .
. , функции
, функции 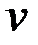 , вариаций
, вариаций  и
и  и производных
и производных 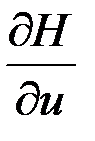 имеют вид:
имеют вид: ,
, ,
, ,
,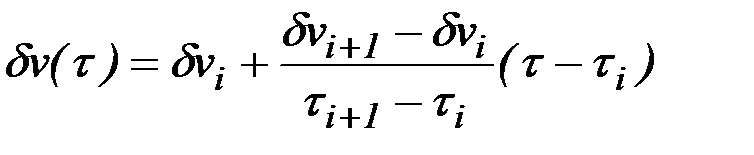 ,
,
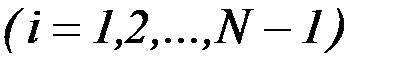 ,
, ,
,  ,
,  ,
, 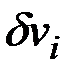 ,
,  - значения величин в узловых точках
- значения величин в узловых точках  .
. и
и  в узловых точках вычисляются по формулам:
в узловых точках вычисляются по формулам: ,
, ,
,  обеспечивается при
обеспечивается при
 ,
,
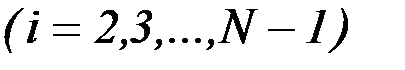 .
. обеспечивается заданием ограничений
обеспечивается заданием ограничений  ,
,  где
где 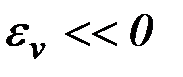 .
. и
и  вычисляются по формулам:
вычисляются по формулам: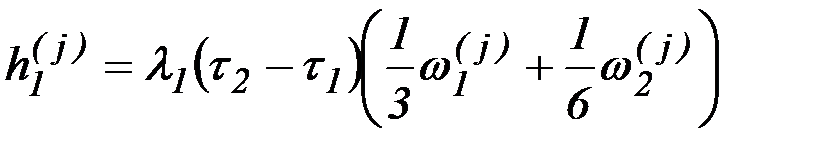 ,
,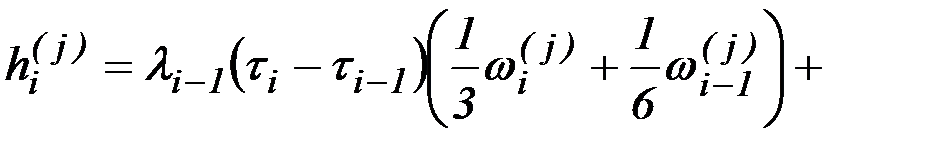
 ,
, ,
,
 ,
, ,
, (6.20) без использования метода плавающих узлов равна
(6.20) без использования метода плавающих узлов равна 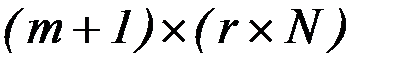 , где
, где  - число функционалов задачи,
- число функционалов задачи,  - размерность вектора управлений,
- размерность вектора управлений, 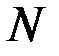 - число узловых точек аппроксимации, то при использовании метода плавающих узлов общая размерность матриц
- число узловых точек аппроксимации, то при использовании метода плавающих узлов общая размерность матриц 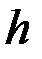 и
и  (6.33) увеличивается до
(6.33) увеличивается до  .
.


