Рассмотрим задачу Лагранжа, полагая, что система и функционал не зависят явно от времени, а на вектор 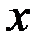 ограничения не накладываются:
ограничения не накладываются:
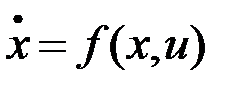 ,
,  ,
,  ,
,  , (3.4)
, (3.4)
 . (3.5)
. (3.5)
Введем в рассмотрение расширенный вектор  , где компонент
, где компонент  является решением уравнения
является решением уравнения
 ,
,  .
.
Таким образом, размерность вектора  равна
равна  . Тогда задача принимает частный вид задачи Майера:
. Тогда задача принимает частный вид задачи Майера:
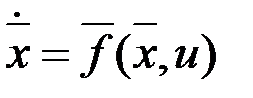 ,
,  ,
,  ,
,  , (3.6)
, (3.6)
 , (3.7)
, (3.7)
где  ,
,  .
.
Пусть 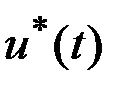 - искомое оптимальное управление, а
- искомое оптимальное управление, а  - соответствующая ему траектория (рис. 3.3):
- соответствующая ему траектория (рис. 3.3):
 ,
,  ,
,  ,
,  .
.
В дальнейшем будем полагать, что  относится к классу кусочно-непрерывных функций, т.е. может иметь конечное число точек разрыва первого рода. Дадим игольчатую вариацию управлению на бесконечно малом интервале
относится к классу кусочно-непрерывных функций, т.е. может иметь конечное число точек разрыва первого рода. Дадим игольчатую вариацию управлению на бесконечно малом интервале  . В результате варьирования дальнейшее движение
. В результате варьирования дальнейшее движение  при
при  будет отличаться от оптимального
будет отличаться от оптимального  (рис. 3.3). Обозначим через
(рис. 3.3). Обозначим через  вариацию траектории
вариацию траектории  .
.
С точностью до малых высшего порядка для момента  будем иметь
будем иметь
 . (3.8)
. (3.8)
Так как  - бесконечно малая величина, то возмущенная траектория будет бесконечно мало отличаться от оптимальной. Поэтому для определения вариации
- бесконечно малая величина, то возмущенная траектория будет бесконечно мало отличаться от оптимальной. Поэтому для определения вариации  при
при  можно воспользоваться уравнением в вариациях
можно воспользоваться уравнением в вариациях
 ,
,  .
.
Рис. 3.3. Траектории движения системы
Интегрируя, можно получить вариацию траектории  для любого
для любого  , в том числе и для
, в том числе и для  , т.е.
, т.е.  . Но вариация
. Но вариация 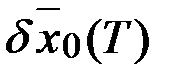 характеризует изменение функционала
характеризует изменение функционала  за счет игольчатой вариации управления. Так как
за счет игольчатой вариации управления. Так как  обеспечивает минимум
обеспечивает минимум  , то
, то  или
или
 , (3.9)
, (3.9)
где  - вектор размерности вектора
- вектор размерности вектора  , подобранный так, чтобы скалярное произведение
, подобранный так, чтобы скалярное произведение  и
и 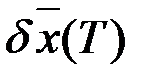 равнялось
равнялось  . Для этого достаточно положить
. Для этого достаточно положить
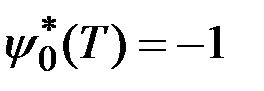 ,
,  . (3.10)
. (3.10)
Поставим задачу найти вектор  , который удовлетворял бы для любого
, который удовлетворял бы для любого  условию:
условию:
 . (3.11)
. (3.11)
Продифференцируем по времени:
 .
.
Учитывая уравнение в вариациях, получим
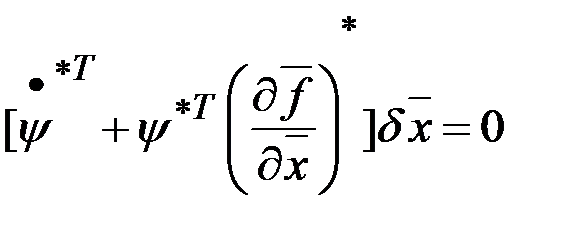 .
.
Так как это равенство должно выполняться для любого  , то получим следующее дифференциальное уравнение для вектора
, то получим следующее дифференциальное уравнение для вектора  :
:
 .
.
Это уравнение может быть решено лишь совместно с исходной системой, т.к. в него входят  и
и  .
.
Перепишем соотношение (3.11) для  с учетом (3.10)
с учетом (3.10)
 .
.
Раскрывая его с помощью (3.8), получим
 . (3.12)
. (3.12)
Введем в рассмотрение функцию  - гамильтониан
- гамильтониан
 .
.
Тогда (3.12) можно представить в виде
 .
.
Т.к.  может быть любым из
может быть любым из  , то окончательно
, то окончательно
 (3.13)
(3.13)
для любого  .
.
Если учесть, что
 ,
, 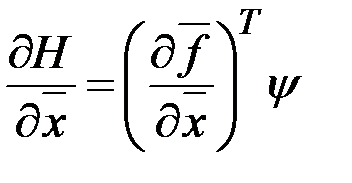 ,
,
то уравнения, определяющие  и
и  на оптимальной траектории при
на оптимальной траектории при  могут быть представлены в виде
могут быть представлены в виде
 ,
,  . (3.14)
. (3.14)
Эта система является канонической. Заметим, что она с точностью до обозначений совпадает с канонической формой уравнения Эйлера. Граничными условиями для нее являются условия трансверсальности:
 ,
,  ,
,  . (3.15)
. (3.15)
Принцип максимума Понтрягина формулируется следующим образом. Необходимое условие оптимальности для задачи (3.6) заключается в существовании такого вектора 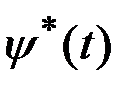 , который совместно с
, который совместно с  являлся бы решением канонической системы (3.14) с граничными условиями (3.15), а гамильтониан
являлся бы решением канонической системы (3.14) с граничными условиями (3.15), а гамильтониан  в каждый момент времени достигал бы своего максимального значения по
в каждый момент времени достигал бы своего максимального значения по  , т.е. выполнялось бы условие (3.13).
, т.е. выполнялось бы условие (3.13).
Свойства гамильтониана
На оптимальной траектории гамильтониан обладает следующими свойствами.
1. Гамильтониан  - непрерывная функция времени для всех
- непрерывная функция времени для всех  .
.
Это свойство очевидно для любого  , не совпадающего с точками разрыва управления
, не совпадающего с точками разрыва управления 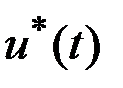 . Пусть
. Пусть  - одна из точек разрыва. Рассмотрим значения
- одна из точек разрыва. Рассмотрим значения  слева и справа от точки
слева и справа от точки  . В силу непрерывности по времени
. В силу непрерывности по времени 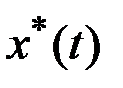 и
и  можно записать
можно записать
 .
.
 ,
,
 .
.
 .
.
Предположим, что  . Возможны два случая:
. Возможны два случая:  и
и 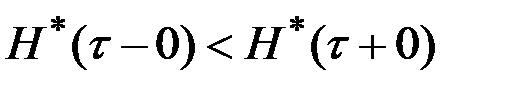 или
или
 .
.
 ,
,
 .
.
 .
.
И то и другое противоречит основной теореме принципа максимума, согласно которой гамильтониан всегда принимает максимальное значение. Следовательно,  , то есть функция
, то есть функция  непрерывна.
непрерывна.
2. Гамильтониан постоянен на оптимальной траектории, т.е.  для всех
для всех  .
.
Рассмотрим некоторый отрезок  , на котором функция
, на котором функция  непрерывна. Для любых
непрерывна. Для любых  в силу основной теоремы принципа максимума
в силу основной теоремы принципа максимума

и поэтому
 .
.
Если  , то
, то
 .
.
При  получаем неравенство
получаем неравенство
 .
.
Правая часть равна нулю, что следует из канонической системы уравнений. Следовательно,
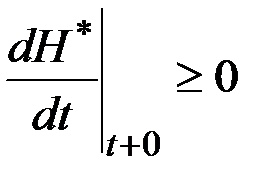 . (3.16)
. (3.16)
Если 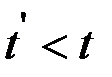 , то аналогично можно получить, что
, то аналогично можно получить, что
 . (3.17)
. (3.17)
Из (3.16) и (3.17) следует, что 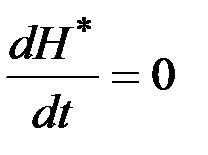 , т.е.
, т.е.  для всех
для всех  . В силу непрерывности
. В силу непрерывности  по времени
по времени  для всех
для всех  .
.
3. Если  свободно, то
свободно, то  для всех
для всех  .
.
Проварьируем управление в конечный момент времени  , изменив величину
, изменив величину 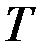 на бесконечно малую величину
на бесконечно малую величину  и сохранив при этом величину
и сохранив при этом величину  . В отличие от игольчатой такая вариация называется временной вариацией управления. Видно, что вариация траектории
. В отличие от игольчатой такая вариация называется временной вариацией управления. Видно, что вариация траектории  с точностью до малых высшего порядка будет равна
с точностью до малых высшего порядка будет равна
 .
.
Умножив на  с учетом (3.9), получим
с учетом (3.9), получим
 .
.
Т.к.  может быть положительным и отрицательным, то
может быть положительным и отрицательным, то
 .
.
Гамильтониан на всей оптимальной траектории постоянен, поэтому
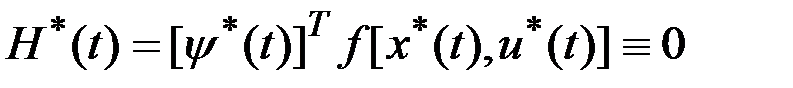
для всех  .
.





 ограничения не накладываются:
ограничения не накладываются: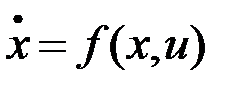 ,
,  ,
,  ,
,  , (3.4)
, (3.4) . (3.5)
. (3.5) , где компонент
, где компонент  является решением уравнения
является решением уравнения ,
,  .
. равна
равна  . Тогда задача принимает частный вид задачи Майера:
. Тогда задача принимает частный вид задачи Майера: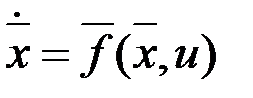 ,
,  ,
,  ,
,  , (3.6)
, (3.6) , (3.7)
, (3.7) ,
,  .
.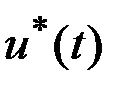 - искомое оптимальное управление, а
- искомое оптимальное управление, а  - соответствующая ему траектория (рис. 3.3):
- соответствующая ему траектория (рис. 3.3): ,
,  ,
,  ,
,  .
. относится к классу кусочно-непрерывных функций, т.е. может иметь конечное число точек разрыва первого рода. Дадим игольчатую вариацию управлению на бесконечно малом интервале
относится к классу кусочно-непрерывных функций, т.е. может иметь конечное число точек разрыва первого рода. Дадим игольчатую вариацию управлению на бесконечно малом интервале  . В результате варьирования дальнейшее движение
. В результате варьирования дальнейшее движение  при
при  будет отличаться от оптимального
будет отличаться от оптимального  (рис. 3.3). Обозначим через
(рис. 3.3). Обозначим через  вариацию траектории
вариацию траектории  .
. будем иметь
будем иметь . (3.8)
. (3.8) - бесконечно малая величина, то возмущенная траектория будет бесконечно мало отличаться от оптимальной. Поэтому для определения вариации
- бесконечно малая величина, то возмущенная траектория будет бесконечно мало отличаться от оптимальной. Поэтому для определения вариации  при
при  можно воспользоваться уравнением в вариациях
можно воспользоваться уравнением в вариациях ,
,  .
.


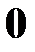
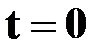
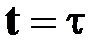




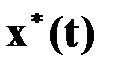

 для любого
для любого  , в том числе и для
, в том числе и для  , т.е.
, т.е.  . Но вариация
. Но вариация 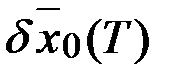 характеризует изменение функционала
характеризует изменение функционала  за счет игольчатой вариации управления. Так как
за счет игольчатой вариации управления. Так как  обеспечивает минимум
обеспечивает минимум  , то
, то  или
или , (3.9)
, (3.9) - вектор размерности вектора
- вектор размерности вектора  , подобранный так, чтобы скалярное произведение
, подобранный так, чтобы скалярное произведение  и
и 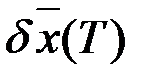 равнялось
равнялось  . Для этого достаточно положить
. Для этого достаточно положить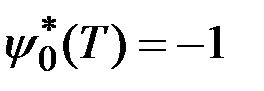 ,
,  . (3.10)
. (3.10) , который удовлетворял бы для любого
, который удовлетворял бы для любого  условию:
условию: . (3.11)
. (3.11) .
.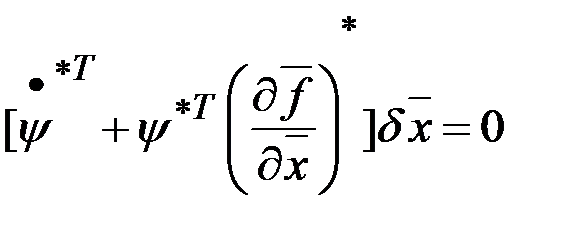 .
. , то получим следующее дифференциальное уравнение для вектора
, то получим следующее дифференциальное уравнение для вектора  :
: .
. и
и  .
. с учетом (3.10)
с учетом (3.10) .
. . (3.12)
. (3.12) - гамильтониан
- гамильтониан .
. .
. может быть любым из
может быть любым из  , то окончательно
, то окончательно (3.13)
(3.13) .
. ,
, 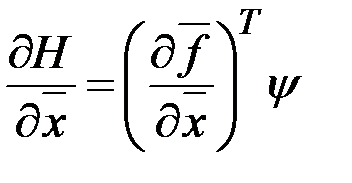 ,
, и
и  на оптимальной траектории при
на оптимальной траектории при  могут быть представлены в виде
могут быть представлены в виде ,
,  . (3.14)
. (3.14) ,
,  ,
,  . (3.15)
. (3.15)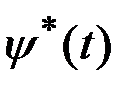 , который совместно с
, который совместно с  являлся бы решением канонической системы (3.14) с граничными условиями (3.15), а гамильтониан
являлся бы решением канонической системы (3.14) с граничными условиями (3.15), а гамильтониан  в каждый момент времени достигал бы своего максимального значения по
в каждый момент времени достигал бы своего максимального значения по  , т.е. выполнялось бы условие (3.13).
, т.е. выполнялось бы условие (3.13). - непрерывная функция времени для всех
- непрерывная функция времени для всех  .
. , не совпадающего с точками разрыва управления
, не совпадающего с точками разрыва управления 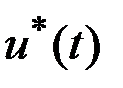 . Пусть
. Пусть  - одна из точек разрыва. Рассмотрим значения
- одна из точек разрыва. Рассмотрим значения  слева и справа от точки
слева и справа от точки  . В силу непрерывности по времени
. В силу непрерывности по времени 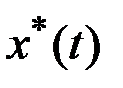 и
и  можно записать
можно записать .
. ,
, .
. .
. . Возможны два случая:
. Возможны два случая:  и
и 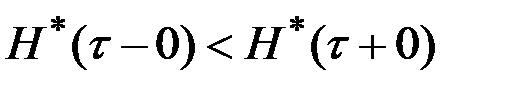 или
или .
. ,
, .
. .
. , то есть функция
, то есть функция  для всех
для всех  .
. , на котором функция
, на котором функция  непрерывна. Для любых
непрерывна. Для любых  в силу основной теоремы принципа максимума
в силу основной теоремы принципа максимума
 .
. , то
, то .
. получаем неравенство
получаем неравенство .
.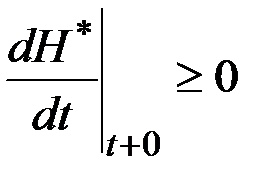 . (3.16)
. (3.16)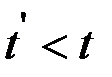 , то аналогично можно получить, что
, то аналогично можно получить, что . (3.17)
. (3.17)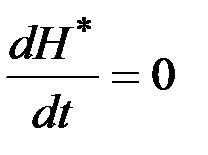 , т.е.
, т.е.  для всех
для всех  . В силу непрерывности
. В силу непрерывности  по времени
по времени  для всех
для всех  .
. свободно, то
свободно, то  для всех
для всех  .
. , изменив величину
, изменив величину 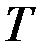 на бесконечно малую величину
на бесконечно малую величину  и сохранив при этом величину
и сохранив при этом величину  . В отличие от игольчатой такая вариация называется временной вариацией управления. Видно, что вариация траектории
. В отличие от игольчатой такая вариация называется временной вариацией управления. Видно, что вариация траектории  с точностью до малых высшего порядка будет равна
с точностью до малых высшего порядка будет равна .
. с учетом (3.9), получим
с учетом (3.9), получим .
. может быть положительным и отрицательным, то
может быть положительным и отрицательным, то .
.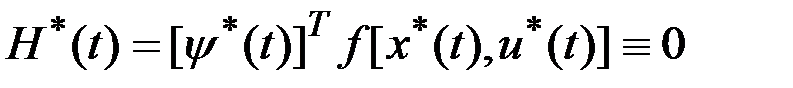
 .
.


