Основным инструментом теоретического анализа задач оптимального управления и разработки методов их приближенного решения является способ вычисления производных от входящих в постановку задачи функционалов по управлению
 .
.
На информации о значениях функциональных производных основан переход к улучшенному управлению при выполнении каждой итерации метода последовательной линеаризации.
Существует процедура дифференцирования функционалов, определенных на траекториях управляемой системы, вида:
 , (6.9)
, (6.9)
 , (6.10)
, (6.10)
где 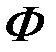 - заданная достаточно гладкая функция своих аргументов;
- заданная достаточно гладкая функция своих аргументов;  - заданная точка на
- заданная точка на  .
.
Функционалы вида (6.9), (6.10) называются дифференцируемыми в смысле Фреше.
Часто встречающиеся в задачах управления движением функционалы вида:
 , (6.11)
, (6.11)
 , (6.12)
, (6.12)
не имеют производных Фреше. Они дифференцируемы в некотором специальном смысле - по направлениям в функциональном прострастве (по Гато).
При численном решении задач функционалы, дифференцируемые по Гато, заменяются одним или аппроксимируются с помощью специальных процедур несколькими функционалами, дифференцируемыми по Фреше.
Способ дифференцирования функционалов вида (6.9), (6.10) сводится к расчету по следующим соотношениям.
Элементы матрицы  частных производных
частных производных 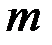 функционалов Фреше по
функционалов Фреше по 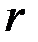 управляющим воздействиям размерности
управляющим воздействиям размерности  вычисляются по формуле:
вычисляются по формуле:
 , (6.13)
, (6.13)
где  - сопряженная матрица размерности
- сопряженная матрица размерности  частных производных правых частей уравнений (6.1) по управляющим воздействиям;
частных производных правых частей уравнений (6.1) по управляющим воздействиям;  - матрица размерности
- матрица размерности  частных производных функций
частных производных функций 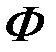 , входящих в выражения для функционалов, по управляющим воздействиям
, входящих в выражения для функционалов, по управляющим воздействиям  .
.
Элементы матрицы сопряженных переменных  размерности
размерности 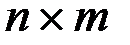 являются решением сопряженной системы дифференциальных уравнений:
являются решением сопряженной системы дифференциальных уравнений:
 , (6.14)
, (6.14)
где  - сопряженная матрица размерности
- сопряженная матрица размерности 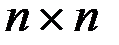 частных производных правых частей уравнений (6.1) по фазовым координатам;
частных производных правых частей уравнений (6.1) по фазовым координатам;  - матрица размерности
- матрица размерности  .
.
Для функционалов вида (6.9) 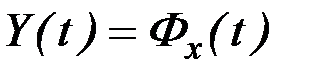 , где
, где  - сопряженная матрица размерности
- сопряженная матрица размерности  частных производных функций
частных производных функций 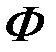 по фазовым координатам
по фазовым координатам  . Система уравнений (6.14) интегрируется справа налево с граничным условием
. Система уравнений (6.14) интегрируется справа налево с граничным условием  .
.
Для функционалов вида (6.10)  ,
,  , а система (6.14) интегрируется справа налево с граничным условием
, а система (6.14) интегрируется справа налево с граничным условием  , причем
, причем  при
при  .
.
Для функционалов вида
 , (6.15)
, (6.15)
с помощью которых задаются ограничения на фазовые координаты и режимы движения в любой точке, элементы матрицы функциональных производных и сопряженных переменных вычисляются в соответствии с (6.13) и (6.14), причем 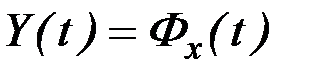 .
.
Система (6.14) интегрируется справа налево с граничным условием 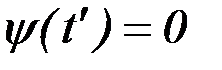 , причем
, причем  при
при  .
.
Таким образом, для дифференцирования функционалов вида (6.9), (6.10) и (6.15) необходимо проинтегрировать слева направо систему уравнений (6.1) и справа налево сопряженную систему уравнений (6.14), а также провести сложение, вычитание и перемножение матриц в соответствии с приведенными соотношениями.



 .
. , (6.9)
, (6.9) , (6.10)
, (6.10)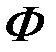 - заданная достаточно гладкая функция своих аргументов;
- заданная достаточно гладкая функция своих аргументов;  - заданная точка на
- заданная точка на  .
. , (6.11)
, (6.11) , (6.12)
, (6.12) частных производных
частных производных 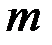 функционалов Фреше по
функционалов Фреше по 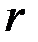 управляющим воздействиям размерности
управляющим воздействиям размерности  вычисляются по формуле:
вычисляются по формуле: , (6.13)
, (6.13) - сопряженная матрица размерности
- сопряженная матрица размерности  частных производных правых частей уравнений (6.1) по управляющим воздействиям;
частных производных правых частей уравнений (6.1) по управляющим воздействиям;  - матрица размерности
- матрица размерности  частных производных функций
частных производных функций  .
. размерности
размерности 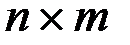 являются решением сопряженной системы дифференциальных уравнений:
являются решением сопряженной системы дифференциальных уравнений: , (6.14)
, (6.14) - сопряженная матрица размерности
- сопряженная матрица размерности 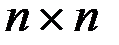 частных производных правых частей уравнений (6.1) по фазовым координатам;
частных производных правых частей уравнений (6.1) по фазовым координатам;  - матрица размерности
- матрица размерности  .
.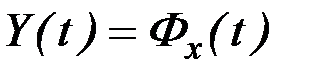 , где
, где  - сопряженная матрица размерности
- сопряженная матрица размерности  частных производных функций
частных производных функций  . Система уравнений (6.14) интегрируется справа налево с граничным условием
. Система уравнений (6.14) интегрируется справа налево с граничным условием  .
. ,
,  , а система (6.14) интегрируется справа налево с граничным условием
, а система (6.14) интегрируется справа налево с граничным условием  , причем
, причем  при
при  .
. , (6.15)
, (6.15)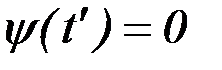 , причем
, причем 


