В общем виде ограничения в виде неравенств на управление  записываются следующим образом:
записываются следующим образом:
 , (6.34)
, (6.34)
 . (6.35)
. (6.35)
Рассматриваемые методы формирования управления основаны на построении минимизирующей последовательности управлений. Поиск в пространстве управлений позволяет относительно просто учитывать ограничения на управление любой степени сложности, включая ограничения на величину управляющего воздействия, скорость его изменения и другие характеристики управляющей зависимости по каждому из каналов управления.
Рассмотрим в общем виде способы учета ограничений на управление вида (6.34), (6.35) при реализации численных методов формирования управления по  -ому каналу
-ому каналу 
 .
.
Учет ограничений на управляющие зависимости вида (6.34) осуществляется на каждой итерации улучшения управления следующим образом.
1. С помощью численных методов и алгоритмов на основе последовательной линеаризации в узлах аппроксимации задачи вычисляются улучшенные значения управляющей зависимости 
 без учета ограничений (6.34).
без учета ограничений (6.34).
2. Последовательно проверяется, начиная с первого узла, выполнение неравенств:

 ,
,
где 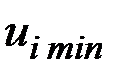 и
и 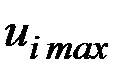 - значения заданных функций
- значения заданных функций  и
и  в узлах аппроксимации.
в узлах аппроксимации.
В узлах, в которых эти ограничения не выполняются, значения управляющих зависимостей заменяются на 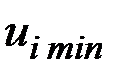 или
или 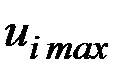 .
.
3. В качестве нового улучшенного опорного управления принимается зависимость, удовлетворяющая ограничениям (6.34).
Учет ограничений на управляющие зависимости вида (6.35) осуществляется на каждой итерации улучшения управления следующим образом.
1. В узлах аппроксимации задачи вычисляются улучшенные значения управляющих зависимостей 
 без учета ограничений (6.35).
без учета ограничений (6.35).
2. Последовательно проверяется, начиная с интервала между первым и вторым узлом, выполнение неравенств:

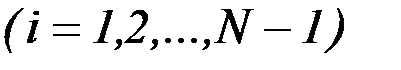 .
.
Здесь 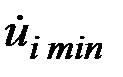 и
и  - значения заданных функций
- значения заданных функций  и
и 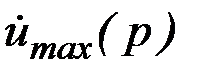 в узлах аппроксимации.
в узлах аппроксимации.
На интервалах, на которых эти ограничения не выполняются, производится перерасчет значений управляющих зависимостей в конце интервала. Если 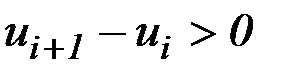 , то перерасчет производится по одной из следующих формул:
, то перерасчет производится по одной из следующих формул:
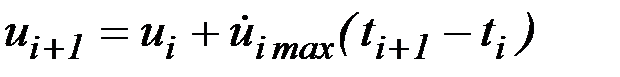 ,
,

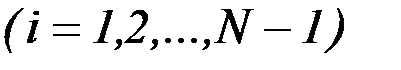 .
.
Если  , то перерасчет производится по одной из следующих формул:
, то перерасчет производится по одной из следующих формул:
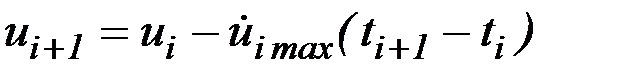 ,
,

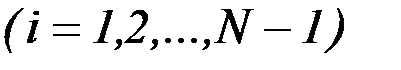 .
.
3. В качестве нового улучшенного управления принимается зависимость, удовлетворяющая ограничениям (6.35).
Поскольку рассчитанное на итерации неисправленное улучшенное управление принадлежит малой окрестности  опорного управления, а учет рассматриваемых ограничений не расширяет область
опорного управления, а учет рассматриваемых ограничений не расширяет область  , то предлагаемые способы учета ограничений на управляющие зависимости не вносят дополнительных погрешностей в процесс поиска управления, удовлетворяющего всем условиям задачи.
, то предлагаемые способы учета ограничений на управляющие зависимости не вносят дополнительных погрешностей в процесс поиска управления, удовлетворяющего всем условиям задачи.
Рассмотрим как учитываются ограничения на управление в виде равенств:
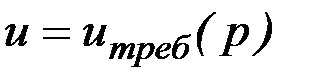 , (6.36)
, (6.36)
 . (6.37)
. (6.37)
Учет ограничений на управляющие зависимости вида (6.36) осуществляется на каждой итерации улучшения управления следующим образом.
1. С помощью разрабатываемых численных методов на основе последовательной линеаризации в узлах аппроксимации задачи вычисляются улучшенные значения управляющей зависимости 
 без учета ограничений (6.36).
без учета ограничений (6.36).
2. Последовательно проверяется, начиная с первого узла, выполнение равенства (6.36):

 ,
,
где  - значения заданной функции
- значения заданной функции  в узлах аппроксимации.
в узлах аппроксимации.
В узлах, в которых это равенство не выполняется, значения управляющих зависимостей заменяются на  .
.
3. В качестве нового улучшенного опорного управления принимается зависимость, удовлетворяющая ограничениям (6.36).
Учет ограничений на управляющие зависимости вида (6.37) осуществляется на каждой итерации улучшения управления следующим образом.
1. В узлах аппроксимации задачи вычисляются улучшенные значения управляющих зависимостей 
 без учета ограничений (6.37).
без учета ограничений (6.37).
2. Последовательно проверяется, начиная с интервала между первым и вторым узлом, выполнение равенств:
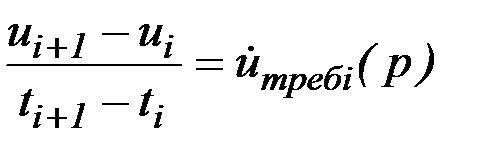
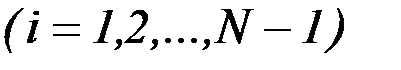 ,
,
где  - значения заданной функции
- значения заданной функции  в узлах аппроксимации.
в узлах аппроксимации.
На интервалах, на которых эти ограничения не выполняются, производится перерасчет значений управляющих зависимостей в конце интервала. Если 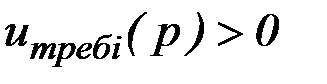 , то перерасчет производится по формуле:
, то перерасчет производится по формуле:

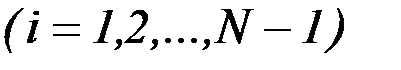 .
.
Если 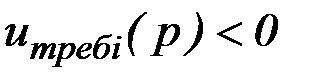 , то перерасчет производится по формуле:
, то перерасчет производится по формуле:

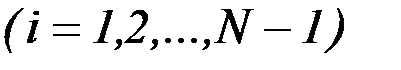 .
.
3. В качестве нового улучшенного управления принимается зависимость, удовлетворяющая ограничениям (6.37).





 записываются следующим образом:
записываются следующим образом: , (6.34)
, (6.34) . (6.35)
. (6.35) -ому каналу
-ому каналу 
 .
.
 без учета ограничений (6.34).
без учета ограничений (6.34).
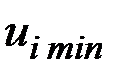 и
и 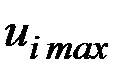 - значения заданных функций
- значения заданных функций  и
и  в узлах аппроксимации.
в узлах аппроксимации.
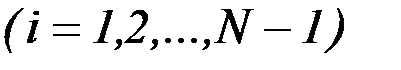 .
.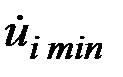 и
и  - значения заданных функций
- значения заданных функций  и
и 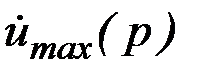 в узлах аппроксимации.
в узлах аппроксимации.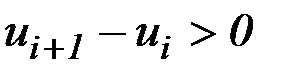 , то перерасчет производится по одной из следующих формул:
, то перерасчет производится по одной из следующих формул: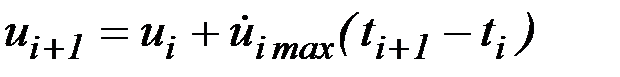 ,
,
 , то перерасчет производится по одной из следующих формул:
, то перерасчет производится по одной из следующих формул: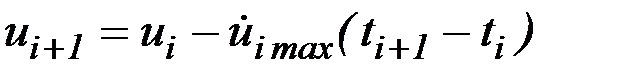 ,
,
 опорного управления, а учет рассматриваемых ограничений не расширяет область
опорного управления, а учет рассматриваемых ограничений не расширяет область 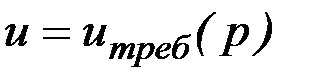 , (6.36)
, (6.36) . (6.37)
. (6.37)
 - значения заданной функции
- значения заданной функции  в узлах аппроксимации.
в узлах аппроксимации.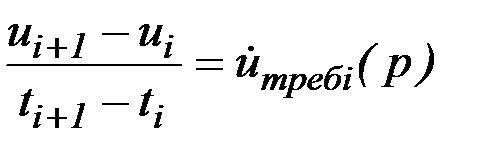
 - значения заданной функции
- значения заданной функции  в узлах аппроксимации.
в узлах аппроксимации.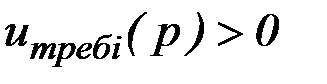 , то перерасчет производится по формуле:
, то перерасчет производится по формуле:
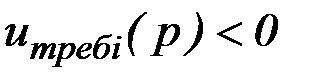 , то перерасчет производится по формуле:
, то перерасчет производится по формуле:



