РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
Объект исследования: вещественное число 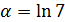 .
.
Результаты, полученные лично автором: произведен поиск многочленов для определения оценки меры иррациональности 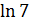 .
.
Мерой иррациональности 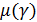 вещественного числа
вещественного числа 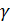 называется нижняя грань множества чисел
называется нижняя грань множества чисел 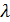 , для которых, начиная с некоторого положительного
, для которых, начиная с некоторого положительного 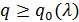 , выполняется неравенство
, выполняется неравенство
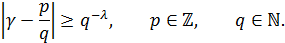
В 2007 г. К. Ву получил результат оценки меры иррациональности числа 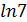
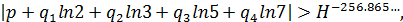
где 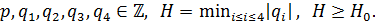
Из данного неравенства при 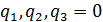 следует оценка
следует оценка
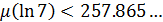
Целью исследования является улучшение последней оценки и усовершенствования алгоритма вычисления оценки меры иррациональности. При использовании нового подхода интегральная конструкция основывается на симметризованных многочленах. Некоторые из них были вычислены с помощью программы, реализованной на языке C++ с использованием библиотеки для работы с большими числами NTL.
Искомые квадратичные многочлены имеют следующий вид:
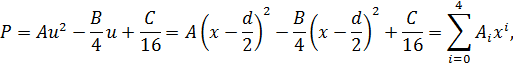
где
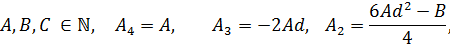
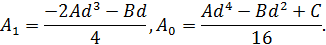
Для оптимизации перебора коэффициентов многочленов используются ограничения значений показателей, проверка принадлежности корней требуемым отрезкам и отсечение части диапазона поиска. Вычисления осуществляются в параллельном режиме.
В результате выполнения программы и анализа выходных наборов значений были выделены многочлены, подходящие по условиям задачи. Добавление их в общую конструкцию позволило получить новую оценку меры иррациональности, которая составила 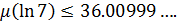
Материал поступил в редколлегию 27.04.2017
УДК 511.36
А.В. Волкова
Научный руководитель: доцент кафедры «Высшая математика»,
к. ф.-м. н. Е.С.  Золотухина
Золотухина
ПОЛУЧЕНИЕ ПРЕДСТАВЛЕНИЯ ИНТЕГРАЛА В ВИДЕ ЛИНЕЙНОЙ ФОРМЫ ОТ 1 И 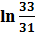 С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Объект исследования: симметризованный интеграл.
Результаты, полученные лично автором: получено представление интеграла в виде линейной формы от 1 и 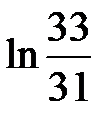 с целыми коэффициентами.
с целыми коэффициентами.
В последние годы был улучшен ряд важных оценок мер иррациональности значений некоторых действительных чисел. Доказательства этих результатов чаще всего используют интегральные конструкции, дающие малые линейные формы от логарифмов и других чисел. Большой интерес представляют симметризованные интегралы.
Цель работы – получить представление симметризованного интеграла в виде линейной формы от 1 и 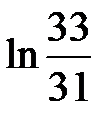 с целыми коэффициентами.
с целыми коэффициентами.
Рассмотрим интеграл
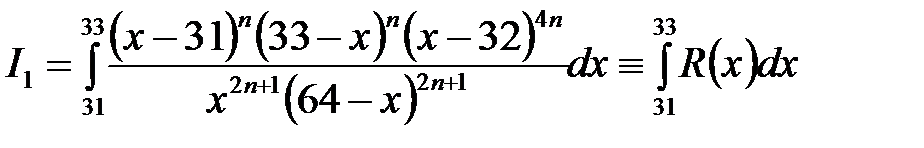 , (1)
, (1)
где 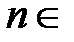 N,
N, 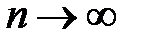 .
.
Подынтегральная функция 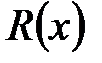 обладает свойством симметрии
обладает свойством симметрии
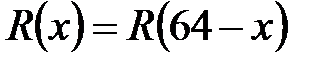 ,
,
ввиду которого справедливо следующее разложение 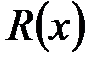 в сумму простейших дробей
в сумму простейших дробей
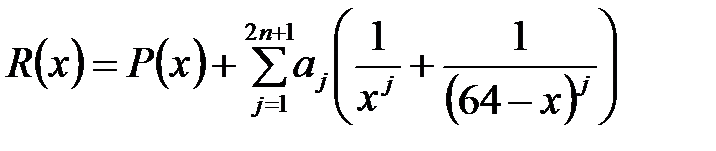 ,
, 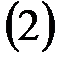
где 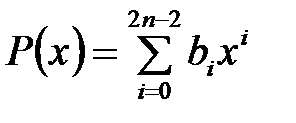 ,
, 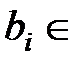 Z,
Z, 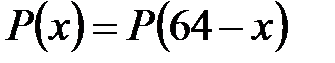 ,
,
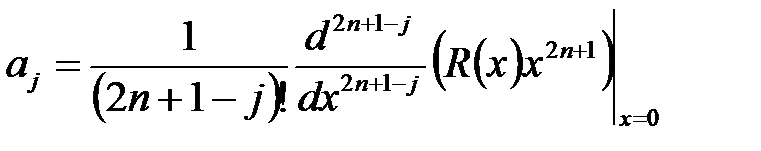 .
.
Впервые подобный по структуре интеграл был использован В.Х.  Салиховым для улучшения оценки меры иррациональности числа
Салиховым для улучшения оценки меры иррациональности числа 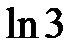 .
.
Пусть далее 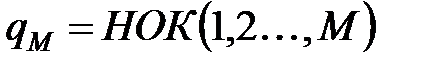 для
для 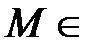 N.
N.
Коэффициенты 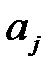 разложения
разложения 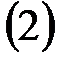 можно определить в следующей лемме.
можно определить в следующей лемме.
Лемма  1.
1.  Для всех
Для всех 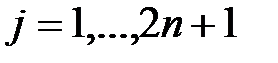 справедливо представление
справедливо представление
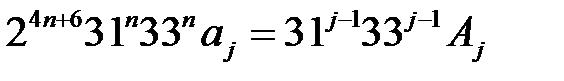 ,
, 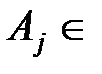 Z.
Z.
Используя лемму 1, интеграл 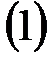 можно представить в виде линейной формы от 1 и
можно представить в виде линейной формы от 1 и 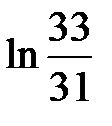 с целыми коэффициентами.
с целыми коэффициентами.
Лемма  2.
2.  Справедливо представление вида
Справедливо представление вида
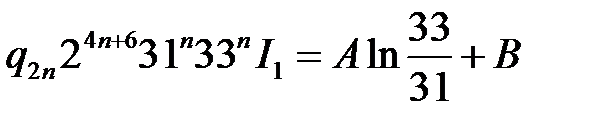 , где
, где 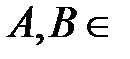 Z. (3)
Z. (3)
С помощью представления (3) может быть получена оценка меры иррациональности числа 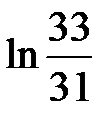 .
.
Материал поступил в редколлегию 17.04.17
УДК 519.2
А.Ю. Волкова, Ю.О. Савраскина
Научный руководитель: ассистент кафедры «Высшая математика»,
А.О. Алейникова





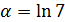 .
.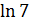 .
.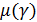 вещественного числа
вещественного числа 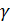 называется нижняя грань множества чисел
называется нижняя грань множества чисел 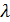 , для которых, начиная с некоторого положительного
, для которых, начиная с некоторого положительного 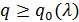 , выполняется неравенство
, выполняется неравенство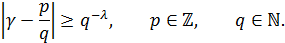
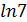
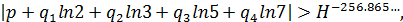
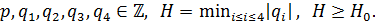
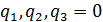 следует оценка
следует оценка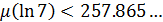
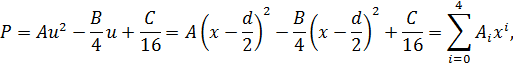
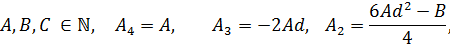
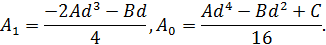
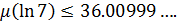
 Золотухина
Золотухина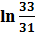 С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ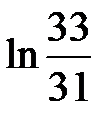 с целыми коэффициентами.
с целыми коэффициентами.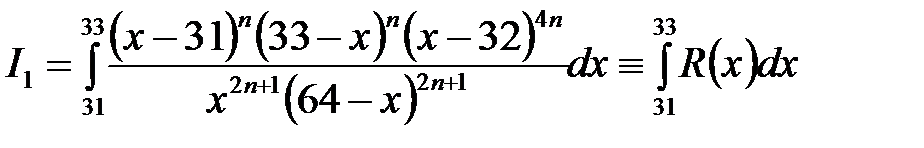 , (1)
, (1)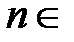 N,
N, 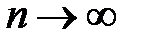 .
.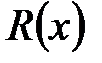 обладает свойством симметрии
обладает свойством симметрии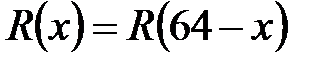 ,
,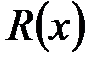 в сумму простейших дробей
в сумму простейших дробей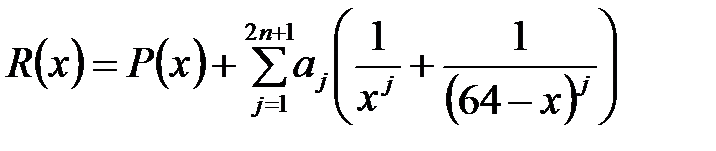 ,
, 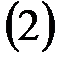
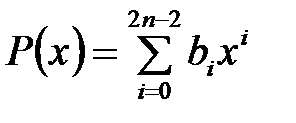 ,
, 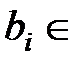 Z,
Z, 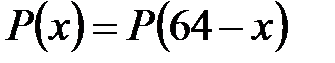 ,
,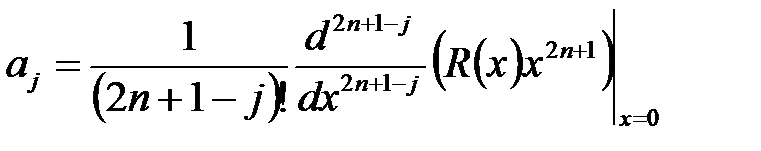 .
.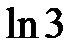 .
.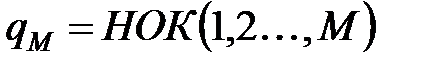 для
для 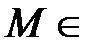 N.
N.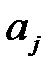 разложения
разложения 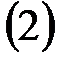 можно определить в следующей лемме.
можно определить в следующей лемме. 1.
1. 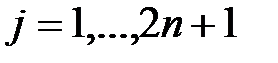 справедливо представление
справедливо представление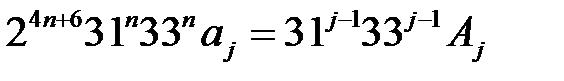 ,
, 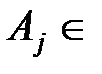 Z.
Z.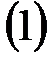 можно представить в виде линейной формы от 1 и
можно представить в виде линейной формы от 1 и 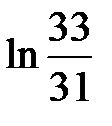 с целыми коэффициентами.
с целыми коэффициентами.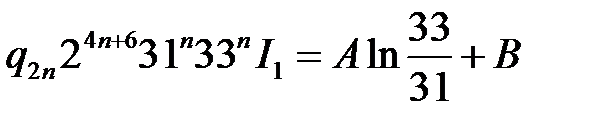 , где
, где 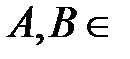 Z. (3)
Z. (3)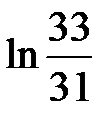 .
.


