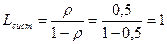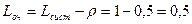На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной кабиной, очередь на прием к врачу, очередь на проезд по мосту при движении с одной полосой, очередь на входе в автобус при наличии устройства автоматизированного контроля проезда пассажиров и т.д.). Итак, имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность  , а поток обслуживаний – интенсивность
, а поток обслуживаний – интенсивность  . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
. Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
Система может находиться в одном из состояний s0, s1, s2,…, sk,… по числу заявок, находящихся в СМО: s0 – канал свободен, s1- канал занят (обслуживает заявку), очереди нет, s2 – канал занят, одна заявка стоит в очереди,…, sk – канал занят, (k-1) заявок в очереди и т.д.
Граф состояний представлен на рис.6

Прежде чем найти выражения для предельных вероятностей, необходимо быть уверенным в их существовании. Доказано, что если  , т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок в единицу времени, то предельные вероятности существуют. Если
, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок в единицу времени, то предельные вероятности существуют. Если  , то очередь растет до бесконечности.
, то очередь растет до бесконечности.
Предельная вероятность р0 для состояния s0 приобретет вид
 (22)
(22)
Так как  , то в скобках имеет место геометрический ряд, который сходится к сумме, равной
, то в скобках имеет место геометрический ряд, который сходится к сумме, равной  , поэтому
, поэтому  и с учетом формул (10)
и с учетом формул (10)
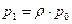 ,
,  ,…,
,…,  ,…
,…
Предельные вероятности других состояний приобретают вид:
 ,
, 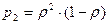 ,…,
,…,  ,… (24)
,… (24)
Предельные вероятности p0, p1,…, pk,… образуют убывающую геометрическую прогрессию со знаменателем  . Следовательно, вероятность p0 – наибольшая. Это означает, что если СМО справляется с потоком заявок (при
. Следовательно, вероятность p0 – наибольшая. Это означает, что если СМО справляется с потоком заявок (при  ), то наиболее вероятным будет отсутствие заявок в системе.
), то наиболее вероятным будет отсутствие заявок в системе.
Вычислим среднее число заявок в системе Lсист. Так как количество заявок может принимать значения 0, 1, 2, 3,…, k,…, то по формуле математического ожидания можно записать

С учетом формул (24)
 (25)
(25)
Можно показать, что формула (7.25) преобразуется при  к виду
к виду
 (26)
(26)
Теперь определим среднее число заявок в очереди (длину очереди) Lоч.
Длина очереди есть разница между общим число заявок в системе и заявками, находящимися на обслуживании, тогда
 ,
,
где Lоб - среднее число заявок, ожидающих обслуживания.
Так как рассматриваемая СМО одноканальная, то обслуживаться может только одна заявка, а остальные заявки ждут своей очереди. Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значение 0 (если канал свободен), либо 1 (если канал занят)
 (27)
(27)
Теперь
 (28)
(28)
Среднее время пребывания заявки в системе (очереди) равно среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т.е.
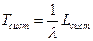 ,
,  (29)
(29)
Формулы (29) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, пребывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность  .
.
С учетом (7.26) и (7.28) имеем
 ,
,  (30)
(30)
Пример 6. На оптовую базу поступают на разгрузку три автомобиля в час (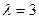 ). Среднее время разгрузки
). Среднее время разгрузки  одного автомобиля 10 мин. Определить эффективность СМО.
одного автомобиля 10 мин. Определить эффективность СМО.
Решение. Имеем одноканальную СМО с неограниченной очередью. Интенсивность обслуживания автомобилей 
Параметр загрузки 
Среднее число обслуживаемых автомобилей
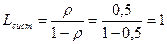
Среднее время обслуживания автомобиля

Длина очереди (среднее число автомобилей, ожидающих разгрузки)
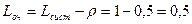
Среднее время ожидания автомобиля в очереди






 , а поток обслуживаний – интенсивность
, а поток обслуживаний – интенсивность  . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
. Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
 , т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок в единицу времени, то предельные вероятности существуют. Если
, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок в единицу времени, то предельные вероятности существуют. Если  , то очередь растет до бесконечности.
, то очередь растет до бесконечности. (22)
(22) , поэтому
, поэтому  и с учетом формул (10)
и с учетом формул (10)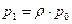 ,
,  ,…,
,…,  ,…
,… ,
, 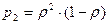 ,…,
,…,  ,… (24)
,… (24)
 (25)
(25) (26)
(26) ,
, (27)
(27) (28)
(28)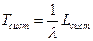 ,
,  (29)
(29) ,
,  (30)
(30)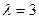 ). Среднее время разгрузки
). Среднее время разгрузки  одного автомобиля 10 мин. Определить эффективность СМО.
одного автомобиля 10 мин. Определить эффективность СМО.