Волгоградский институт бизнеса
Экономико-математические методы и модели
Лекции (конспекты лекций)
Материалы допускаются к использованию в учебном процессе
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Содержание
Тема №1 «Основы математического моделирования социально-экономических систем. Балансовые модели». 3
Тема №2 «Методы оптимизации планирования и управления». 10
Тема №3 «Моделирование систем массового обслуживания». 39
Тема №4 «Прикладные модели экономических процессов». 54
Тема №1 «Основы математического моделирования социально-экономических систем.
Балансовые модели»
План лекции:
Модель Леонтьева многоотраслевой экономики
Продуктивная модель Леонтьева
Примеры решения задач межотраслевого баланса
Продуктивная модель Леонтьева
Матрица  называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора  существует решение
существует решение  уравнение (3).
уравнение (3).
В этом случае и модель Леонтьева, определяемая матрицей  , также называется продуктивной.
, также называется продуктивной.
Существует несколько критериев продуктивности матрицы  . Приведем некоторые из них.
. Приведем некоторые из них.
1. Матрица  продуктивна тогда и только тогда, когда матрица
продуктивна тогда и только тогда, когда матрица  существует и неотрицательна.
существует и неотрицательна.
Пример. Исследовать на продуктивность матрицу

Решение. Матрица  ;
;
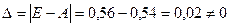 , следовательно, матрица
, следовательно, матрица  не вырождена и имеет обратную
не вырождена и имеет обратную
 .
.
Напомним, что  , где
, где  ,
,  ,
,  ,
,  - алгебраические дополнения элементов матрицы
- алгебраические дополнения элементов матрицы  .
.
Как видно, матрица  существует и неотрицательна. Следовательно, матрица
существует и неотрицательна. Следовательно, матрица  продуктивна.
продуктивна.
2. Матрица  продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем, хотя бы для одного из столбцов сумма элементов, строго меньше единицы, т.е. матрица
продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем, хотя бы для одного из столбцов сумма элементов, строго меньше единицы, т.е. матрица  продуктивна, если
продуктивна, если 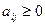 для любых
для любых  и
и  , и существует номер
, и существует номер  такой, что
такой, что  .
.
Пример. Исследовать на продуктивность матрицу 
Решение. Элементы матрицы имеют неотрицательные элементы и удовлетворяют критерию продуктивности:
 .
.
Следовательно, матрица  продуктивна.
продуктивна.
Примеры решения задач межотраслевого баланса
Пример 1. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.
| Отрасль
| Потребление
| Конечный продукт
|
| промышленность
| Сельское хозяйство
|
| производство
| Промышленность
| 0,3
| 0,25
|
|
| Сельское хозяйство
| 0,15
| 0,12
|
|
Найти:
а) плановые объемы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей;
б) необходимый объем валового выпуска каждой отрасли, если конечное потребление продукции сельского хозяйства увеличится на 20%, а промышленности на 10%.
Решение. Матрица коэффициентов прямых затрат  и вектор конечной продукции имеют вид:
и вектор конечной продукции имеют вид:
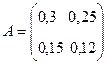 ,
,  .
.
Найдем матрицу 

Матрица полных затрат равна:
 .
.
По формуле (6.5) вычислим вектор валового продукта 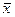 :
:
 .
.
Межотраслевые поставки  найдем по формуле (6.2)
найдем по формуле (6.2)
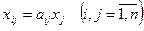 .
.
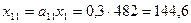 ;
;  ;
;
 ;
;  .
.
Найдем чистую продукцию отраслей.
Чистой продукцией отраслей называется разность между валовой продукцией этой отрасли и затратами продукции всех отраслей на производство этой отрасли.
Для промышленности и сельского хозяйства она соответственно равна:
 ,
,
 .
.
По условию вектор конечного потребления продукции промышленности увеличится на 10%, а сельского хозяйства на 20%
 .
.
Тогда вектор валового продукта 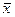 будет равен:
будет равен:
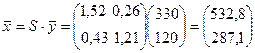 .
.
Таким образом, выпуск в промышленности нужно увеличить до 532,8 усл.ден.ед., а в сельском хозяйстве – до 287,1 усл.ден.ед.
Пример 2. Дана матрица прямых затрат  .
.
Найти: а) вектор валовой продукции 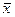 для обеспечения выпуска конечной продукции
для обеспечения выпуска конечной продукции  ;
;
б) приращение вектора 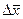 для увеличения выпуска конечной продукции на
для увеличения выпуска конечной продукции на 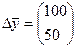 .
.
Решение. а) Матрица 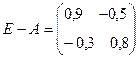

Вектор валовой продукции равен:
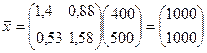 .
.
б) Так как 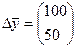 , то вектор выпуска конечной продукции равен
, то вектор выпуска конечной продукции равен  .
.
Вектор валовой продукции при этом равен
 .
.
Следовательно, приращение вектора 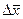 равно
равно 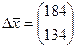 .
.
Пример 3. Работа системы, состоящей из двух отраслей, в течение некоторого периода характеризуется следующими данными (усл.ден.ед.):
| Отрасль
| потребление
| Чистая продукция
|
| I
| II
|
| I
|
|
|
|
| II
|
|
|
|
Вычислить матрицу прямых затрат.
Решение. Чистая продукция отраслей равна соответственно
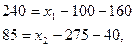
Где  - валовой продукт отраслей I и II.
- валовой продукт отраслей I и II.
Отсюда,  ,
,  .
.
Межотраслевые поставки 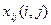 определяются по формулам
определяются по формулам  ,откуда
,откуда
 ,
, 
 ,
,  .
.
Таким образом, матрица прямых затрат имеет вид:  .
.
Тема №2 «Методы оптимизации планирования и управления»
План лекции:
Геометрия выпуклых множеств
Шаг. Целевая функция.
Прибыль от реализации всей продукции можно представить в виде:
 .
.
Геометрия выпуклых множеств
Множество, элементами которого являются точки, называется точечным. Примерами точечных множеств на плоскости являются: треугольник, угол, точки прямой (или прямая), отрезок, луч, круг и т.д. В пространстве – параллелепипед, призма, шар и т.п.
Различают выпуклые и невыпуклые точечные множества.
Определение. Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их.
В противном случае множество называется невыпуклым (рис. 1)

выпуклое невыпуклое
Рис. 5.1
Выпуклые множества обладают важным свойством: пересечение (общая часть) двух выпуклых множеств также выпуклое множество.
Точка выпуклого множества называется угловой (или крайней), если через нее нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.
Для выпуклого многоугольника угловыми точками являются все его вершины, для отрезка – его концы.
Рассмотрим геометрическую интерпретацию множества допустимых решений системы линейных уравнений на конкретном примере.
Дано уравнение  . Рассматривая уравнение как систему, состоящую из одного уравнения с двумя неизвестными, найти:
. Рассматривая уравнение как систему, состоящую из одного уравнения с двумя неизвестными, найти:
- множество допустимых решений;
- угловые точки этого множества;
- базисные решения.
Решение. Каждое решение данного уравнения – пара чисел, а геометрически – точка на плоскости. Множество всех его решений – прямая. Неотрицательным решениям данной системы (состоящей из одного уравнения) соответствуют точки отрезка АВ, т.е. выпуклое множество с двумя угловыми точками А и В (рис. 2). Итак, множеством допустимых решений системы из одного уравнения с двумя переменными оказался выпуклый многоугольник.


Рис. 2
Найдем базисные решения системы. Принимая х1 за основную переменную (тогда х2 – неосновная) и полагая в уравнении х2=0, получим х1=5. Первое базисное решение (5;0).
Если за основную переменную принять х2, то получим второе базисное решение (0;2). Оба базисных решения допустимы. Им соответствуют угловые точки множества допустимых решений системы (рис. 5.2).
Еще пример. Дано уравнение  . Строим прямую по данному уравнению (рис. 3).
. Строим прямую по данному уравнению (рис. 3).

Координаты ее точек служат решениями этого уравнения. Неотрицательным решениям соответствуют точки луча АС – выпуклого множества с одной угловой точкой А (1;0). Найдем базисные решения системы. Если принять х1 за основную переменную, то получим базисное решение (1;0). Если же за основную переменную примем х2, то второе базисное решение (0;-1) не является допустимым.
Обратим внимание на то, что между угловыми точками и допустимыми базисными решениями системы существует однозначное соответствие: число угловых точек множества равно числу допустимых базисных решений системы. Оказывается, эта закономерность носит общий характер.
Теперь рассмотрим геометрическую интерпретацию множества решений линейного неравенства с двумя переменными.
В общем виде линейное неравенство с двумя переменными записываются в виде
 (8)
(8)
или
 (9)
(9)
Каждому решению неравенств, т.е. паре чисел (х1, х2) соответствует точка на плоскости, а множеством решений линейного неравенства (8) служит одна из двух полуплоскостей, на которую всю плоскость делит прямая  , включая и эту прямую, а другая полуплоскость вместе с прямой является множеством решений неравенства (9).
, включая и эту прямую, а другая полуплоскость вместе с прямой является множеством решений неравенства (9).
Рассмотрим ряд примеров.
Пример 1. Построить множество решений неравенства  .
.
 Решение. Искомое множество решений состоит из решений уравнения
Решение. Искомое множество решений состоит из решений уравнения  и строгого неравенства
и строгого неравенства 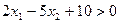 . Решениями уравнения служат точки прямой
. Решениями уравнения служат точки прямой  , которая построена на рис.4.
, которая построена на рис.4.


Множество решений строгого неравенства – одна из плоскостей, на которые делит плоскость прямая АВ. Какая из них является искомой, выясняют с помощью контрольной точки, в качестве которой удобно брать начало координат. Действительно, подставляя в неравенство координаты начала координат, получим 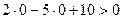 , т.е. оно выполняется. Следовательно, множеством решений строгого неравенства служит нижняя полуплоскость, т.к. она содержит начало координат, а решением исходного неравенства – полуплоскость вместе с прямой.
, т.е. оно выполняется. Следовательно, множеством решений строгого неравенства служит нижняя полуплоскость, т.к. она содержит начало координат, а решением исходного неравенства – полуплоскость вместе с прямой.
Пример 2. Построить множество решений системы линейных неравенств

Решение.
1) Строим прямую 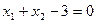 . Подстановка начала координат как контрольной точки дает -3<0, т.е. оно выполняется. Множество решений первого неравенства – нижняя полуплоскость вместе с прямой I.
. Подстановка начала координат как контрольной точки дает -3<0, т.е. оно выполняется. Множество решений первого неравенства – нижняя полуплоскость вместе с прямой I.
2) Строим прямую  и множество решений второго неравенство это верхняя полуплоскость с прямой II.
и множество решений второго неравенство это верхняя полуплоскость с прямой II.
3) Строим прямую  . Она проходит через начало координат (в уравнении отсутствует свободный член). Вторую точку найдем, полагая, например,
. Она проходит через начало координат (в уравнении отсутствует свободный член). Вторую точку найдем, полагая, например, 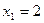 , тогда
, тогда  . В качестве контрольной точки возьмём точку (0;2). Множество решений неравенства – нижняя полуплоскость с прямой III.
. В качестве контрольной точки возьмём точку (0;2). Множество решений неравенства – нижняя полуплоскость с прямой III.
4) Строим прямую  . Значение
. Значение  лежит левее этой прямой, что и определяет полуплоскость решений неравенства
лежит левее этой прямой, что и определяет полуплоскость решений неравенства  .
.
5) Двойное неравенство  эквивалентно системе двух неравенств
эквивалентно системе двух неравенств  и
и 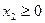 . Неравенству
. Неравенству  соответствует полуплоскость, расположенная ниже прямой
соответствует полуплоскость, расположенная ниже прямой  ; соответственно для
; соответственно для 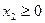 – полуплоскость, лежащая выше оси абсцисс (рис. 5).
– полуплоскость, лежащая выше оси абсцисс (рис. 5).

Следовательно, множество решений системы из всех пяти неравенств – выпуклый многоугольник ABCDEF с конечным числом угловых точек. Координаты точек A, B, C, D, E, F могут быть найдены как координаты пересечения соответствующих прямых. Например, точка А является точкой пересечения прямых I и V. Решая совместно уравнения этих прямых, получим

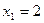 ;
; 

В заключение сформулируем основные теоремы линейного программирования, базирующиеся на геометрии выпуклых множеств.
Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.
Теорема 2. Если существует, и притом единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений.
Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений, и наоборот, каждой угловой точке множества допустимых решений системы ограничений соответствует допустимое базисное решение.
Основные понятия теории массового обслуживания
СМО с отказами
СМО с очередью
Основные понятия теории массового обслуживания
Во многих областях экономики имеются системы, осуществляющие многократное выполнение однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Примерами таких систем можно считать банки, налоговые инспекции, аудиторские службы, системы связи, автозаправочные станции, различные организации и предприятия торгового и бытового обслуживания и т.п.
Каждая СМО состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые называют каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы, операторы и др. По числу каналов СМО подразделяются на одноканальные и многоканальные.
Заявки поступают в СМО обычно не регулярно, а случайно, образуя так называемый случайный поток заявок (требований). Обслуживание заявок также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными), в другие же периоды СМО работает с недогрузкой или простаивает.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоками заявок.
В качестве показателей эффективности СМО используются: среднее число заявок, обслуживаемых в единицу времени; среднее число заявок в очереди; среднее время ожидания обслуживания; вероятность отказа в обслуживании без ожидания; вероятность того, что число заявок в очереди превысит определенное значение и т.п.
Цель теории массового обслуживания заключается в разработке рекомендаций по оптимальной организации работы СМО и регулировании потока заявок для обеспечения высокой эффективности их функционирования.
СМО делятся на два основных типа:
- СМО с отказами;
- СМО с ожиданием (очередью).
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, телефонная станция. Если вызываемы абонент занят, то требование на соединение с ним получает отказ и теряется).
В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.
СМО с отказами
СМО с очередью
Управление товарными запасами. Основные понятия
Основные понятия теории игр. Классификация игр. Формальное представление игр
Основные понятия теории игр. Классификация игр. Формальное представление игр
При решении задач по теории оптимизации рассматривались такие задачи принятие решений, когда выбор решения осуществляется одним лицом. В подобных задачах рационального ведения хозяйства решение выбирается при предположении о том, что известны целевая функция, различные способы действия и ограничения. Рассмотрим задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого из субъектов зависит от решений принимаемых всеми остальными участниками. Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия.
Конфликт может возникнуть также из различия целей, которые отражают не только не совпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица.
Всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, т.е. описывать:
А) множество заинтересованных сторон (обычно их называют игроками, они еще именуются субъектами, лицами, сторонами, участниками). В случае если число игроков конечно, они различаются по своим номерам (1-й игрок, 2-й игрок и т.д.), или по присваемым им именам (например, Продавец и Покупатель в ситуации монополии – монопсонии);
Б) возможные действия каждый из сторон, именуемым также стратегиями или ходами;
В) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.
В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общественны, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функции выигрыша и стратегии всех остальных игроков, и в соответствии с этой информацией организует свое поведение.
Формализация содержательного описания конфликта представляет собой его математическую модель, которую называют игрой.
Классификация игр.
Различные виды игр можно классифицировать, основываясь на том или ином принципе:
- по числу игроков;
- по числу стратегий;
- по свойствам функций выигрыша;
- по возможностям предварительных переговоров;
- взаимодействия между игроками в ходе игры.
По числу игроков различают игры с двумя, тремя и более участниками. В принципе возможны так же игры с бесконечным числом игроков.
По количеству стратегий различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий. Сами стратегии в конечных играх нередко называют чистыми стратегиями.
В бесконечных играх игроки имеют бесконечное число возможных стратегий, так в ситуации Продавец-Покупатель каждый из игроков может назвать любую цену и количество продаваемого (покупаемого) товара.
По свойствам функции выигрыша (платежных функций) – возможна ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. на лицо конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Прямой противоположностью такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно так, что им выгодно действовать сообща.
Между эти крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.
В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.
Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях.
Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной. Очевидно, что все антагонистические игры могут служить примером некооперативных игр.
Формальное представление игр
Множество всех игроков, обозначаемое I, в случае их конечного числа может задаваться простым перечислением игроков. Например, I=(1,2) при игре в орлянку; I=(1,2,…,n) в случае анализа результатов голосования.
Множество стратегий игрока i обозначим через xi. При игре в орлянку каждый игрок располагает двумя стратегиями: xi=(орел, решка). Каждый участник голосования имеет выбор на множестве стратегий [За, Против].
Покупатель и продавец могут назначать некоторую неотрицательную цену на продаваемый (покупаемый) товар, т.е. множество стратегий каждого из них: xi; p0>0. В каждой партии игрок выбирает свою стратегию xi, в результате чего оказывается набор стратегий x=(x1, x2,…, xn), называемых ситуацией.
Ситуация в парламенте описывает список (за, за, против, за,…), полученный в итоге голосования.
Заинтересованность игроков в ситуациях проявляется в том, что каждому игроку i в каждой ситуации х приписывается число, выражающее степень удовлетворения его интересов в данной ситуации. Это число называется выигрышем игрока i и обозначается через hi(x), а соответствие между набором ситуаций и выигрышем I называется функцией выигрыша (платежной функцией) этого игрока Hi.
В случаях конечной игры двух лиц функции выигрыша каждого из игроков удобно представить в виде матрицы выигрышей, где строки представляют стратегии одного игрока, столбцы – стратегии другого игрока, а в клетках матрицы указывают выигрыши каждого из игроков в каждой из образующихся ситуаций. (Данная форма представления конечных игр двух лиц объясняет общее для них название – матричные игры).
Например, в случае игры в орлянку каждый из игроков имеет по две стратегии Орел и Решка. Если оба игрока выбирают одинаковые стратегии, первый игрок выигрывает 1 рубль, а второй проигрывает рубль. В случае, когда оба игрока выбирают различные стратегии, первый игрок проигрывает один рубль, второй выигрывает один рубль.
Матрица выигрышей первого игрока
| Стратегии первого игрока
|
| Стратегии второго игрока
|
|
| Орел
| Решка
| H1
|
| Орел
|
| -1
|
| Решка
| -1
|
|
Матрица выигрышей второго игрока
| Стратегии первого игрока
|
| Стратегии второго игрока
|
|
| Орел
| Решка
| H2
|
| Орел
| -1
|
|
| Решка
|
| -1
|
Для антагонистических игр выполняется соотношение H1=-H2
Для наглядности обе матрицы совмещают в одну:
| Стратегии первого игрока
|
| Стратегии второго игрока
|
|
| Орел
| Решка
|
| Орел
| 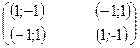
|
| Решка
|
Рассмотрим пример записи функции для бесконечной игры. Для случая двух игроков, каждый из игроков может объявить цену pi, по которой он хотел бы продать некоторое количество товара. При этом предполагается, что потребители приобретают товар у фирмы, объявившей меньшую цену, или распределят свой спрос между фирмами в случае, если они назначили одинаковую цену.
Если функцию спроса в зависимости от цены на товар обозначить – d(p), то функция выигрыша первой фирмы П1(p1,p2) будет выглядеть:

Семейный спор.
Согласно условиям этой игры семейная пара Муж и Жена каждый вечер решают проблему: как им провести свой досуг. В городке, где они живут, имеется два вида развлечений: Балет и Футбол. У каждого из супругов есть свое любимое зрелище: Жена предпочитает – балет, Муж – футбол.
Однако супруги так привязаны друг к другу, что посещение любимого развлечения в одиночку доставляет им совсем не такое удовольствие как присутствие на них вдвоем, т.е е если Жена идет вечером на балет с Мужем, она получает максимум удовольствия (4 единицы). Муж недолюбливает балет, но присутствие на нем с Женой спрашивает тягостное времяпровождение (1 единица). История повторяется с точностью до наоборот, когда Жена идет с Мужем на обожаемый им футбол.
Муж получает (4 единицы), Жена получает (1 единицу). В принципе Муж может сходить на Футбол один, а жена в одиночку сходить на балет (за это они получат по 2 единицы). И вечер будет испорчен, если Муж пойдет на футбол, а жена на балет (0 единиц).
В итоге матрица выигрышей описанной игры будет:
|
Муж
| Жена
|
|
| Балет
| Футбол
|
| Балет
| 
|
| Футбол
|
Можно показать, что если супруги будут придерживаться различных несогласованных стратегий, множество возможных выигрышей образует в системе треугольник 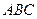 с вершинами в точках
с вершинами в точках 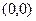 ,
,  ,
,  .
.

Линия  - множество Парето - оптимальных решений. Вдоль этой линии рост удовольствий Жены, возможен только за счет снижения удовольствия Мужа.
- множество Парето - оптимальных решений. Вдоль этой линии рост удовольствий Жены, возможен только за счет снижения удовольствия Мужа.
Точка 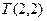 - является точкой угрозы в этой игре. Например, «угроза» со стороны Жены может звучать: «Вместо того чтобы более
- является точкой угрозы в этой игре. Например, «угроза» со стороны Жены может звучать: «Вместо того чтобы более 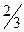 своего свободного времени проводить на этом футболе, а буду ходить на балет (с Мужем или без него – неважно) – ничего не потеряю.
своего свободного времени проводить на этом футболе, а буду ходить на балет (с Мужем или без него – неважно) – ничего не потеряю.
Аналогично может звучать «угроза» - Мужа.
Переговорное множество, образуемое точкой угрозы  , представлено линией
, представлено линией 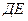 , образуемое точкой угрозы
, образуемое точкой угрозы  , представлено линией
, представлено линией 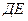 , на Парето - оптимальном множестве решений
, на Парето - оптимальном множестве решений  . На линии
. На линии 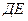 Муж и Жена могут договариваться, как часто они будут бывать вместе на одном из зрелищ, но при этом, во избежание взаимных угроз ни одному из развлечений не должны уделить более своих свободных вечеров.
Муж и Жена могут договариваться, как часто они будут бывать вместе на одном из зрелищ, но при этом, во избежание взаимных угроз ни одному из развлечений не должны уделить более своих свободных вечеров.
Решение Нэша, когда максимально произведение приростов удовольствия Мужа и Жены по сравнению с удовольствием от независимого посещения Футбола и Балета, представлено точкой  - супруги договариваться половину своего свободного времени проводить вместе на балете, вторую половину – на футболе.
- супруги договариваться половину своего свободного времени проводить вместе на балете, вторую половину – на футболе.
Позиционные игры
Рассмотрим пример анализа рыночного поведения с помощью теории игр, когда задача по своей структуре несколько отличается от задач рассмотренных ранее.
Предположим следующую ситуацию.
На рынке некоторого продукта доминирует производитель (Фирма 1), и монопольное положение приносит ему 12 млрд. руб. прибыли. Высокая прибыль в данном секторе привлекает других производителей, в частности фирма 2 решает вопрос: построить ли ей свое предприятие и начать на нем производство такого же товара? Однако известно: что Фирма 1 может предпринять некоторые действия в ответ на вторжение.
С одной стороны Фирма 1 может снизить объем своего производства, уступая часть рынка Фирме 2, и деля с ней прибыль – так как это происходило на примере фирм – олигополистов. В этом случае каждая из фирм получит по 6 млрд. руб. прибыли.
С другой стороны фирма 1 может сохранить объем производства. В этом случае рост совокупного предложения товара фирмами 1 и 2 снизит цену на этот товар, и как следствие прибыль Фирмы 1 упадет до 5 млрд. руб. Одновременно снижение цен приведет к тому, что Фирма 2, сделавшая предварительные затраты для выхода на новый для нее рынок, понесет чистые убытки: она потеряет на этом деле 2 млрд. руб.
В случае если Фирма 2 воздерживается от вступления на рынок, она ничего не выигрывает и не проигрывает (ее прибыль 0 млрд. руб.), а Фирма 1 продолжает получать прибыль в 12 млрд. руб.
Если же Фирма 1 вдруг решит в этой ситуации снизить объем своего производства, ее прибыль упадет до 8 млрд. руб.
В принципе сформированная неантагонистическая игра двух лиц может быть описана следующей матрицей выигрышей (первыми указаны выигрыши фирмы 1 в млрд.руб.)
| Стратегия Фирмы 1
|
Сохранить объем производства


| Снизить объем производства


|
Замечание. Описанная игра по своим условиям отличается от рассмотренных ранее. В предыдущих задач игроки принимали свои решения одновременно, не зная о решении партнера (это весьма существенно), то в данной игре Фирма 1 принимает решения, уже зная о решении избранном Фирмой 2, в ответ она действия Фирмы 2, и это в корне меняет ситуацию.
Игры подобного класса, где задается последовательность принятия решений игроками, называются позиционными играми. Число игроков и шагов в них может равняться 2 (как в рассмотренном примере), 3 и т.д. К позиционным многошаговым играм двух лиц, где игроки принимают решения, зная обо всех предыдущих решениях партнера, можно отнести, например, шахматы и шашки.
В силу отмеченных особенностей структуру позиционной игры более наглядно представляет дерево решений (или в общем случае граф решений), приводящее игроков из исходной позиции в конечные.
Описанную игру Вступление на рынок можно представить следующим деревом, ветви которого соответствуют решениям партнеров, а у каждой из висячих вершин указаны выигрыши игроков (первыми указаны выигрыши Фирмы 1, в млрд. руб.).
В позиционной игре необходимо учитывать, что Фирма 1 принимает решение, уже зная о решении, принятом Фирмой 2, которая должна сделать первый шаг. При этом менеджеры Фирмы 2 могут привести доводы: «Если мы не вступим на рынок со своей продукцией, то в любом случае ничего не потеряем. С другой стороны, если мы решим внедрить на рынок, не исключено, что Фирма сохранит объем производства и для нас это обернется потерями 2 млрд. руб. Поэтому если следовать принципу максимизации своего минимального выигрыша Фирма 2 должна было бы избрать стратегию «Воздержаться от вступления на рынок» (в этом случае прибыль 0 млрд. руб.>-2 млрд. руб.)».
Эти, казалось бы, логичные рассуждения не учитывают одной из главных предпосылок теории игр – предположения о рациональном поведении игроков, стремящихся к максимизации своих выигрышей. В данном случае это заставляет менеджеров фирмы 2 задать себе вопрос: «А насколько вероятна реализация Фирмой 1 стратегии «Сохранить производство», если мы вторгнемся на рынок?» Ведь в этом случае Фирма 1 получит меньшую прибыль (5 млрд. руб.), чем в случае, если она снизит объем своего произ





 называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора  существует решение
существует решение  уравнение (3).
уравнение (3). , также называется продуктивной.
, также называется продуктивной. существует и неотрицательна.
существует и неотрицательна.
 ;
;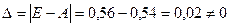 , следовательно, матрица
, следовательно, матрица  не вырождена и имеет обратную
не вырождена и имеет обратную .
. , где
, где  ,
,  ,
,  ,
,  - алгебраические дополнения элементов матрицы
- алгебраические дополнения элементов матрицы 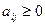 для любых
для любых  и
и  , и существует номер
, и существует номер  такой, что
такой, что  .
.
 .
.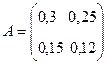 ,
,  .
.
 .
.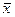 :
: .
. найдем по формуле (6.2)
найдем по формуле (6.2)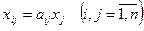 .
.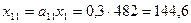 ;
;  ;
; ;
;  .
. ,
, .
. .
.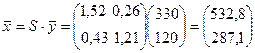 .
. .
. ;
;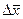 для увеличения выпуска конечной продукции на
для увеличения выпуска конечной продукции на 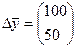 .
.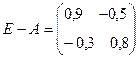

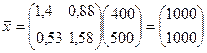 .
. .
. .
.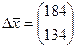 .
.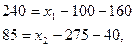
 - валовой продукт отраслей I и II.
- валовой продукт отраслей I и II. ,
,  .
.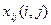 определяются по формулам
определяются по формулам  ,откуда
,откуда ,
, 
 ,
,  .
. .
. .
.
 . Рассматривая уравнение как систему, состоящую из одного уравнения с двумя неизвестными, найти:
. Рассматривая уравнение как систему, состоящую из одного уравнения с двумя неизвестными, найти:

 . Строим прямую по данному уравнению (рис. 3).
. Строим прямую по данному уравнению (рис. 3).
 (8)
(8) (9)
(9) , включая и эту прямую, а другая полуплоскость вместе с прямой является множеством решений неравенства (9).
, включая и эту прямую, а другая полуплоскость вместе с прямой является множеством решений неравенства (9). .
. Решение. Искомое множество решений состоит из решений уравнения
Решение. Искомое множество решений состоит из решений уравнения  и строгого неравенства
и строгого неравенства 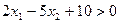 . Решениями уравнения служат точки прямой
. Решениями уравнения служат точки прямой 

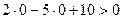 , т.е. оно выполняется. Следовательно, множеством решений строгого неравенства служит нижняя полуплоскость, т.к. она содержит начало координат, а решением исходного неравенства – полуплоскость вместе с прямой.
, т.е. оно выполняется. Следовательно, множеством решений строгого неравенства служит нижняя полуплоскость, т.к. она содержит начало координат, а решением исходного неравенства – полуплоскость вместе с прямой.
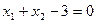 . Подстановка начала координат как контрольной точки дает -3<0, т.е. оно выполняется. Множество решений первого неравенства – нижняя полуплоскость вместе с прямой I.
. Подстановка начала координат как контрольной точки дает -3<0, т.е. оно выполняется. Множество решений первого неравенства – нижняя полуплоскость вместе с прямой I. и множество решений второго неравенство это верхняя полуплоскость с прямой II.
и множество решений второго неравенство это верхняя полуплоскость с прямой II. . Она проходит через начало координат (в уравнении отсутствует свободный член). Вторую точку найдем, полагая, например,
. Она проходит через начало координат (в уравнении отсутствует свободный член). Вторую точку найдем, полагая, например, 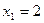 , тогда
, тогда  . В качестве контрольной точки возьмём точку (0;2). Множество решений неравенства – нижняя полуплоскость с прямой III.
. В качестве контрольной точки возьмём точку (0;2). Множество решений неравенства – нижняя полуплоскость с прямой III. . Значение
. Значение  лежит левее этой прямой, что и определяет полуплоскость решений неравенства
лежит левее этой прямой, что и определяет полуплоскость решений неравенства  .
. эквивалентно системе двух неравенств
эквивалентно системе двух неравенств  и
и 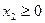 . Неравенству
. Неравенству  ; соответственно для
; соответственно для 


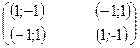


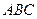 с вершинами в точках
с вершинами в точках 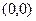 ,
,  ,
,  .
.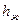

 - множество Парето - оптимальных решений. Вдоль этой линии рост удовольствий Жены, возможен только за счет снижения удовольствия Мужа.
- множество Парето - оптимальных решений. Вдоль этой линии рост удовольствий Жены, возможен только за счет снижения удовольствия Мужа.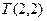 - является точкой угрозы в этой игре. Например, «угроза» со стороны Жены может звучать: «Вместо того чтобы более
- является точкой угрозы в этой игре. Например, «угроза» со стороны Жены может звучать: «Вместо того чтобы более 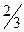 своего свободного времени проводить на этом футболе, а буду ходить на балет (с Мужем или без него – неважно) – ничего не потеряю.
своего свободного времени проводить на этом футболе, а буду ходить на балет (с Мужем или без него – неважно) – ничего не потеряю. , представлено линией
, представлено линией 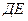 , образуемое точкой угрозы
, образуемое точкой угрозы  - супруги договариваться половину своего свободного времени проводить вместе на балете, вторую половину – на футболе.
- супруги договариваться половину своего свободного времени проводить вместе на балете, вторую половину – на футболе.






