

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Рассмотрим стохастические модели управления запасами, у которых спрос является случайным. Это обстоятельство существенно усложняет модели и их анализ, по этой причине рассмотрим самые простые.
Предположим, что спрос r за интервал времени Т является случайным и задан его закон (ряд) распределения p(r), или плотность вероятностей  (обычно p(r) и
(обычно p(r) и  оценивают на основании опытных или статистических данных).
оценивают на основании опытных или статистических данных).
Если спрос r ниже уровня s, то приобретение (хранение, продажа) излишка продукта требует дополнительных затрат C2 на единицу продукта; если спрос r выше уровня запаса s, то это приводит к штрафу за дефицит C3 на единицу продукта.
В качестве функции суммарных затрат, являющейся в стохастических моделях случайной величины, рассматривают ее среднее значение или математическое ожидание.
В рассматриваемой модели при дискретном случайном спросе r, имеющем закон распределения p(r), математическое ожидание суммарных затрат (учитываем только расходы на неиспользованные единицы продукта) имеет вид:
 (3.28)
(3.28)
В этом выражении первое слагаемое учитывает затраты на приобретение (хранение) излишка единиц продукта s-r (при  ), а второе слагаемое – штраф за дефицит на r-s единиц продукта (при
), а второе слагаемое – штраф за дефицит на r-s единиц продукта (при 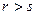 ).
).
В случае непрерывного случайного спроса, задеваемого плотностью вероятностей  , выражение C(s) будет иметь вид:
, выражение C(s) будет иметь вид:
 (3.29)
(3.29)
Задача управления запасами состоит в отыскании такого запаса s, при котором математическое ожидание суммарных затрат (3.28) и (3.29) принимает минимальное значение.
В теории управления операций доказано, что при дискретном случайном спросе r выражение (3.28) минимально при запасе s0 удовлетворяющее неравенством
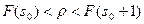 (3.30)
(3.30)
а при непрерывном случайном спросе r выражение (3.29) минимально при значении s0 определяемом из уравнения
 (3.31)
(3.31)
где
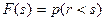 (3.32)
(3.32)
Есть функция распределения спроса r, F(s0) и F(s0+1) – ее значения;  - плотность убытков из-за неудовлетворенного спроса, определяемая
- плотность убытков из-за неудовлетворенного спроса, определяемая 


Оптимальный запас s0 при непрерывном спросе по данному значению  может быть найден графически.
может быть найден графически.
Пример 6. Предприятие закупает агрегат с запасными блоками к нему. Стоимость одного блока равна 5 ден.ед. В случае выхода агрегата из строя из-за поломки блока, отсутствующего в запасе, простой агрегате и срочный заказ нового блока к нему обойдется в 100 ден.ед. Опытное распределение агрегатов по числу блоков, потребовавших замену, представлено в таблице.
| Число замененных блоков r | |||||||
| Статистическая вероятность (доля) агрегатов p(r), которым потребовалась замена r блоков | 0,9 | 0,05 | 0,02 | 0,01 | 0,01 | 0,01 | 0,00 |
Необходимо определить оптимальное число запасных блоков, которое следует приобрести вместе с агрегатом.
Решение. По условию задачи с2=5 и с3=100. Плотность убытков из-за нехватки запасных блоков вычислим по формуле  ;
; 
Учитывая 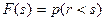 , найдем значения функции распределения спроса.
, найдем значения функции распределения спроса.
| s | >6 | |||||||
| r | >6 | |||||||
| F(s) | 0,00 | 0,00 | 0,9 | 0,95 | 0,97 | 0,98 | 0,99 |
Как следует из таблицы, оптимальный запас составляет s0=3, ибо он удовлетворяет неравенству
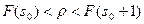
F(3)<0,952<F(4)
Пример 7. Решить задачу 6 при условии непрерывного случайного спроса r, распределенного по показательному закону с функцией распределения  при
при  .
.
Решение. Оптимальное число запасных блоков s0 найдем из уравнения  , т.е.
, т.е.  , если r=s0, то
, если r=s0, то 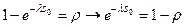
и  при
при 

 блока
блока
В условиях рассматриваемой модели, предположим, что расходование запаса происходит непрерывно с одинаковой относительностью. Эту ситуацию можно представить графически.
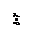




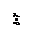

а – соответствует случаю  , когда спрос не превосходит запас
, когда спрос не превосходит запас
б – спрос превышает запас 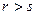 .
.
Замечание: на самом деле график y(t) представляет ступенчатую ломанную, показанную пунктиром, но для исследования модели проще рассматривать y(t) в виде прямой сглаживающей эту ломанную.
Для случая (а) средний запас определяется
 (3.33)
(3.33)
Для случая (б) средний запас с учетом полученной ранее зависимости  ;
;  , в которой полагаем n=r, составляет
, в которой полагаем n=r, составляет
 (3.34)
(3.34)
Средний дефицит продукта за период Т2 для случая (б) при условии n=r 
 (3.35)
(3.35)
Математическое ожидание суммарных затрат будет
 (3.36)
(3.36)
Существует строгое доказательство, что математическое ожидание минимально при s0, удовлетворяющему неравенству
 (3.37)
(3.37)
где  , а
, а  (3.38)
(3.38)
L(s0) и L(s0+1) – значения функции, полученной по формуле (3.38), а F(s) находится как 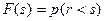 .
.
Пример 8. Имеющиеся на складе изделия равномерно расходуются в течение месяца. Затраты на хранение одного изделия составляют 5 ден.ед., а штраф за дефицит одного изделия обходится в 100 ден.ед. Изучение спроса дало распределение числа потребляемых за месяц изделий представлено в таблице
Необходимо определить оптимальный месячный запас склада.
| Спрос r | 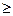 6 6
| ||||||
| Статистическая вероятность p(r) | 0,1 | 0,2 | 0,2 | 0,3 | 0,1 | 0,1 | 0,0 |
Решение: с2=5; с3=100; 
Значение функции L(r) определим с помощью таблицы
| s | r | p(r) | 
| 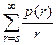
| 
| F(r) | L(r) |
| 0,1 | - | - | - | 0,0 | - | ||
| 0,2 | 0,200 | 0,445 | 0,2225 | 0,1 | 0,325 | ||
| 0,2 | 0,100 | 0,245 | 0,3675 | 0,3 | 0,6675 | ||
| 0,3 | 0,100 | 0,145 | 0,3625 | 0,5 | 0,8625 | ||
| 0,1 | 0,025 | 0,045 | 0,1575 | 0,8 | 0,9575 | ||
| 0,1 | 0,020 | 0,020 | 0,0900 | 0,9 |  0,99 0,99
| ||
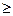 6 6
| 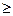 6 6
| 0,000 | 0,000 | 0,000 | 0,000 | 1,0 | 1,000 |
Очевидно, что оптимальный запас изделий s0=3, т.к. он удовлетворяет условию 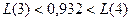 .
.
|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!