Небесная сфера и системы координат .измерение времени.

При изучении видимых движений небесных тел необходимо с той или иной степенью точности определять их положения в моменты наблюдений. При этом нет необходимости знать расстояния до них, поскольку все тела представляются нам как бы находящимися на внутренней поверхности некоторой сферы произвольного радиуса. Поэтому видимые, положения светил можно определять только направлениями, а их взаимное расположение — углами между этими направлениями, или соответствующими дугами больших кругов на сфере, из центра которой исходят все направления.

Воображаемая сфера произвольного радиуса с центром в произвольной точке пространства, на поверхности которой расположены светила так, как они видны на небе в некоторый момент времени из дачной точки пространства, называется небесной сферой.

Таким образом, воображаемый наблюдатель, находящийся в центре небесной сферы, должен видеть положения светил на ее поверхности точно в таком же взаимном расположении, в каком реальный наблюдатель видит реальные светила на небе. Вращение небесной сферы повторяет вращение небесного свода. Небесная сфера служит для изучения видимых положений и движений небесных тел. Для этого на ее поверхности фиксируются основные линии и точки, по отношению к которым и производятся соответствующие измерения.

Небесная сфера и горизонтальная система координат (рис. 1).

Прямая ZOZ' (рис. 1), проходящая через центр О небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения, называется отвесной или вертикальной линией.

Отвесная линия пересекается с поверхностью небесной сферы в двух точках: в зените Z, над головой наблюдателя, и в диаметрально противоположной точке — надире Z'.

Большой круг небесной сферы (SWNE), плоскость которого перпендикулярна к отвесной линии, называется математическим или истинным горизонтом. Математический горизонт делит поверхность небесной сферы на две половины: видимую для наблюдателя, с вершиной в зените Z, и невидимую, с вершиной в надире Z'.

Математический горизонт следует отличать от видимого горизонта (линии, вдоль которой «небо сходится с Землей»). Видимый горизонт на суше — неправильная линия, точки которой лежат то выше, то ниже истинного горизонта. В открытом море видимый горизонт всегда малый круг, плоскость которого параллельна плоскости математического горизонта.

Малый круг небесной сферы (аМа), проходящий через светило М и плоскость которого параллельна плоскости математического горизонта, называется альмукантаратом светила.

Большой полукруг небесной сферы ZMZ', проходящий через зенит, светило М и надир, называется кругом высоты, вертикальным кругом, или просто вертикалом светила.

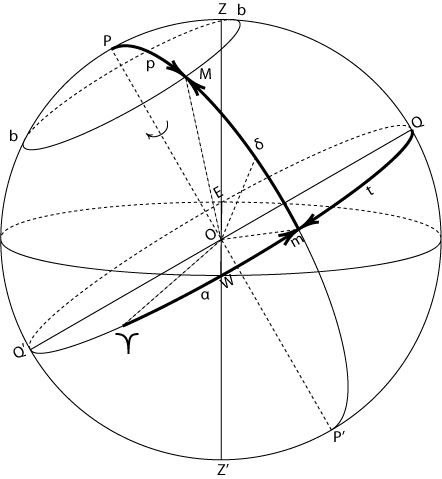
Небесная сфера и экваториальные системы координат (рис. 2).

Диаметр РР' (рис. 2) вокруг которого происходит вращение небесной сферы, называется осью мира. Ось мира пересекается с поверхностью небесной сферы в двух точках: в северном полюсе мира Р и южном полюсе мира Р'. Северный полюс тот, со стороны которого вращение небесной сферы происходит по часовой стрелке, если смотреть на сферу извне. Большой круг небесной сферы QWQ'E, плоскость которого перпендикулярна к оси мира, называется небесным экватором. Небесный экватор делит поверхность небесной сферы на два полушария: северное, с северным полюсом мира Р, и южное, с южным полюсом мира Р'.

Малый круг небесной сферы (bМb), плоскость которого параллельна плоскости небесного экватора, называется небесной или суточной параллелью светила М. Видимые суточные движения светил совершаются по суточным параллелям. Большой полукруг небесной сферы РМР', проходящий через полюсы мира и через светило М, называется часовым кругом или кругом склонения светила. Небесный экватор пересекается с математическим горизонтом в двух точках: в точке востока Е и в точке запада W. Круги высот, проходящие через точки востока и запада, называются первыми вертикалами — восточным и западным. Большой круг небесной сферы PZQSP'Z'Q'N, плоскость которого проходит через отвесную линию и ось мира, называется небесным меридианом. Небесный меридиан делит поверхность небесной сферы на два полушария: восточное, с точкой востока Е, и западное, с точкой запада W. Плоскость небесного меридиана и плоскость математического горизонта пересекаются по прямой линии NOS, которая называется полуденной линией. Небесный меридиан пересекается с математическим горизонтом в двух точках: в точке севера N и в точке юга S. Точкой севера называется та, которая ближе к северному полюсу мира. Точка юга — ближе к южному полюсу мира. Небесный меридиан пересекается с небесным экватором также в двух точках: в верхней точке экватора Q, которая ближе к зениту, и в нижней точке экватора Q', которая ближе к надиру. Дуга небесного меридиана PZQSP' является его верхней частью, а дуга PNQ'Z'P' — нижней.

 

Положение светила на небе, или вообще какой-либо точки на сфере, однозначно определяется по отношению к основным плоскостям и связанным с ними линиям и точкам небесной сферы и выражается количественно двумя величинами (центральными углами или дугами больших кругов), которые называются небесными координатами. Для решения разнообразных задач астрономии пользуются различными системами небесных координат. Системы эти отличаются одна от другой выбором основной плоскости и началом отсчета.

Горизонтальная система. Основной плоскостью в этой системе является плоскость математического горизонта NWSE, а отсчет ведется от зенита и от одной из точек математического горизонта (рис. 1). Одной координатой является или зенитное расстояние z, или высота светила над горизонтом h.

Высотой h светила М называется дуга вертикального круга mМ от математического горизонта до светила, или центральный угол mОМ (в плоскости вертикального круга) между плоскостью математического горизонта и направлением на светило М. Высоты отсчитываются в пределах от 0° до +90° к зениту (если светило находится в видимой части небесной сферы) и от 0° до —90° к надиру (если светило находится в невидимой части небесной сферы).

Зенитным расстоянием z светила М называется дуга вертикального круга ZM от зенита до светила или центральный угол ZOM между отвесной линией и направлением на светило М. Зенитные расстояния отсчитываются в пределах от 0° до 180° в направлении от зенита к надиру. Светила, находящиеся в видимой части небесной сферы, имеют z < 90°, а в невидимой части z > 90°. Между зенитным расстоянием и высотой одного и того же светила всегда справедливо соотношение: z + h = 90°. Светила, находящиеся на одном альмукантарате, имеют одинаковые высоты и одинаковые зенитные расстояния.

Положение же самого вертикального круга на небесной сфере определяется другой координатой — азимутом А. Азимутом А светила М называется дуга математического горизонта Sm от точки юга S до вертикального круга, проходящего через светило, или центральный угол SOm (в плоскости математического горизонта) между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга, проходящего через светило. Азимуты отсчитываются в сторону суточного вращения небесной сферы, т.е. к западу от точки юга S, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу (западные азимуты) и от 0° до -180° (восточные азимуты). В геодезии азимуты отсчитываются от точки севера N либо от 0° до 360° в сторону востока либо от 0° до +180° (восточные азимуты) и от 0° до -180° (западные азимуты). Такие азимуты называются геодезическими, в отличие от астрономических азимутов, отсчитываемых от точки юга. Геодезический азимут А' и астрономический A связаны простым соотношением: А' = А ± 180°. Знак плюс берется для A < 180°, или для отрицательных (восточных) азимутов; знак минус — для А > 180°, или для положительных (западных) азимутов. Светила, находящиеся на одном вертикальном круге, имеют одинаковые азимуты.

Первая экваториальная система координат. Основной плоскостью в этой системе является плоскость небесного экватора QQ', а началом отсчета — точки небесного экватора (рис. 2). Одной координатой является склонение светила δ.

Склонением δ светила М называется дуга mМ часового круга РМmР' от небесного экватора до светила, или центральный угол mОМ (в плоскости часового круга) между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира (светило находится в северном, полушарии небесной сферы) и от 0° до -90° к южному полюсу мира (светило находится в южном полушарии сферы). Иногда, но весьма редко, склонение δ заменяется полярным расстоянием р, т.е. дугой РМ часового круга от северного полюса мира до светила, или центральным углом РОМ между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному. Светила, находящиеся в северном полушарии небесной сферы, имеют р < 90°, а в южном полушарии р > 90°. Между полярным расстоянием и склонением одного и того же светила всегда справедливо соотношение p + δ = 90°. Светила, находящиеся на одной суточной параллели, имеют одинаковые склонения δ и одинаковые полярные расстояния р.

Склонение, или полярное расстояние, определяет положение светила на часовом круге. Положение же самого часового круга на небесной сфере определяется другой координатой — часовым углом t. Часовым углом t светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового круга РМmР', проходящего через светило, или центральный угол QOm (в плоскости небесного экватора), измеряющий двухгранный угол между плоскостями небесного меридиана и часового круга светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, т.е. к западу от верхней точки Q небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу (западные часовые углы) и от 0° до -180° (от 0h до -12h) к востоку (восточные часовые углы). Светила, находящиеся на одном круге склонения, имеют одинаковые часовые углы.

Вторая экваториальная система координат. Основной плоскостью в этой системе является также плоскость небесного экватора, а одной координатой — склонение δ (реже — полярное расстояние р). Другой же координатой, определяющей положение часового круга светила, является прямое восхождение a.

Прямым восхождение α светила М называется дуга небесного экватора Ym (Y — Овен) (см. рис. 2) от точки весеннего равноденствия (Овен) до часового круга, проходящего через светило, или центральный угол YОm (в плоскости небесного экватора) между направлением на точку весеннего равноденствия и плоскостью часового круга светила. Прямые восхождения a отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Светила, находящиеся на одном часовом круге, имеют одинаковые прямые восхождения.

 

Горизонтальные координаты (z, h, А) и часовой угол светила t непрерывно изменяются вследствие суточного вращения небесной сферы, так как они отсчитываются от неподвижных точек, не участвующих в этом вращении. Экваториальные координаты светила (прямое восхождение α и склонение δ) из-за суточного вращения небесной сферы не меняются, так как они отсчитываются от точек небесного экватора, которые сами участвуют в суточном вращении, и следовательно, положение светила относительно этих точек не изменяется. Горизонтальная система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов. Первая экваториальная система (склонение и часовой угол) используется преимущественно при определении точного времени — одной из основных задач практической астрономии. Вторая экваториальная система является основной при решении задач фундаментальной астрометрии. В этой системе составляются списки звездных положений (звездные каталоги) и звездные карты.

Зависимость высоты полюса мира от географической широты места наблюдения. Вращение небесного свода — явление кажущееся и представляет собой следствие действительного вращения Земли вокруг оси в направлении, противоположном суточному вращению неба, т.е. с запада на восток. Поэтому в какой бы точке на поверхности Земли наблюдатель ни находился, он всегда видит вращение небесной сферы происходящим вокруг оси мира — прямой, параллельной оси вращения Земли. Направление же отвесной линии меняется при перемещении наблюдателя по земной поверхности и составляет различные углы с осью вращения. Взаимное расположение кругов и точек небесной сферы, связанных с осью мира и с отвесной линией, зависит, следовательно, от направления последней, т.е. от положения наблюдателя на поверхности Земли. Эта зависимость формулируется в виде следующей теоремы: "высота полюса мира h_P над горизонтом всегда равна астрономической широте ср места наблюдения".

Связь между высотой полюса мира и географической широтой.

Доказательство этого утверждения очевидно из рисунка. φ — это широта, а h_p — это высота северного полюса мира.

Явления, связанные с суточным вращением небесной сферы. Восход и заход светил. Вследствие суточного вращения небесной сферы все светила описывают круги, плоскости которых параллельны плоскости небесного экватора, т.е. они движутся по суточным, или небесным параллелям. В зависимости от географической широты φ места наблюдения и от склонений δ светил суточные параллели последних либо пересекают математический горизонт в двух точках, либо целиком располагаются над ним, либо под ним. Точка пересечения светилом восточной части истинного горизонта называется точкой восхода светила, точка пересечения западной части истинного горизонта — точкой захода светила.

Светило восходит и заходит на данной широте φ, если абcолютное значение его склонения

| δ | < (90° - | φ |).

Если | δ | ≥ (90° - | φ |), то его суточная параллель не пересечет математического горизонта и оно будет либо незаходящим (его суточная параллель располагается целиком над горизонтом) либо невосходящим светилом (его суточная параллель располагается целиком под горизонтом).

Суточная параллель каждого светила пересекает небесный меридиан в двух точках, лежащих на концах диаметра параллели. Явление пересечения светилом небесного меридиана называется кульминацией светила. Кульминация называется верхней, если светило пересекает верхнюю часть PZQSP' небесного меридиана, содержащую Z (рис. 2), и нижней, если светило пересекает нижнюю часть небесного меридиана PNQ'Z'P', содержащую Z'. Различают верхнюю кульминацию к югу от зенита (на дуге ZQSP') и к северу от зенита (на дуге PZ). У светил, не заходящих на данной широте φ, доступны для наблюдений обе кульминации — и верхняя и нижняя; у восходящих и заходящих светил — только верхняя, нижняя кульминация происходит под горизонтом; у невосходящих светил обе кульминации недоступны наблюдениям, так как происходят под горизонтом.

Изменение координат светил при суточном движении. Когда светило восходит или заходит, то его z = 90°, h = 0°, а азимуты точек восхода и захода зависят от склонения светила и широты места наблюдения. В момент верхней кульминации зенитное расстояние светила минимально, высота максимальна, а азимут А = 0 (если светило кульминирует к югу от зенита), или A = 180° (если оно кульминирует к северу от зенита). В момент нижней кульминации зенитное расстояние светила принимает максимальное значение, высота — минимальное, а азимут А = 180°, или А = 0° (если нижняя кульминация происходит между надиром Z' и южным полюсом мира Р'). Следовательно, от нижней кульминации до верхней зенитное расстояние светила уменьшается, а высота увеличивается; от верхней до нижней кульминации, наоборот, зенитное расстояние увеличивается, высота уменьшается. При этом азимут светила также меняется в определенных пределах. Таким образом, горизонтальные координаты светила (z, h и A) непрерывно изменяются вследствие суточного вращения небесной сферы, и если светило неизменно связано со сферой (т.е. его склонение d и прямое восхождение a остаются постоянными), то его горизонтальные координаты принимают свои прежние значения, когда сфера совершит один оборот. Так как суточные параллели светил на всех широтах Земли (кроме полюсов) наклонены к горизонту, то горизонтальные координаты изменяются неравномерно даже при равномерном суточном вращении небесной сферы. Высота светила h и его зенитное расстояние z наиболее медленно меняются близ меридиана, т.е. в момент верхней или нижней кульминаций. Азимут же светила A, наоборот, в эти моменты изменяется наиболее быстро. Часовой угол светила t (в первой экваториальной системе координат), подобно азимуту A, непрерывно меняется. В момент верхней кульминации светила его t = 0. В момент нижней кульминации часовой угол светила t = 180° или 12^h. Но, в отличие от азимутов, часовые углы светил (если их склонения d и прямые восхождения a остаются постоянными) изменяются равномерно, так как они отсчитываются по небесному экватору, и при равномерном вращении небесной сферы изменения часовых углов пропорциональны промежуткам времени, т.е. приращения часовых углов равны углу поворота небесной сферы. Равномерность изменения часовых углов имеет очень важное значение при измерении времени.

Высота светила h или зенитное расстояние z в моменты кульминаций зависят от склонения светила δ и широты места наблюдателя φ. Непосредственно из чертежа (рис. 2) следует:

1. если склонение светила M₁ δ < φ, то оно кульминирует к югу от зенита на зенитном расстоянии z = φ - δ, или на высоте h = 90° - φ + δ;

2. если δ = φ, то светило кульминирует в зените и тогда z = 0 и h = + 90°;

3. если δ > φ, то светило М₂ в верхней кульминации находится к северу от зенита на зенитном расстоянии z = δ - φ, или на высоте h = 90° + φ - δ.

4. наконец, в момент нижней кульминации зенитное расстояние светила М₃ z = 180° - φ - δ, a высота h = δ - (90° - φ) = φ + δ - 90°.

Из наблюдений известно, что на данной широте j каждая звезда всегда восходит (или заходит) в одной и той же точке горизонта, высота ее в меридиане также всегда одинакова. Отсюда можно заключить, что склонения звезд не меняются с течением времени (по крайней мере заметно). Точки же восхода и захода Солнца, Луны и планет, а также их высота в меридиане в разные дни года — различны. Следовательно, склонения этих светил непрерывно меняются с течением времени.

52.Способы посадки и высадки лоцмана. требования. предварительные приготовления. обязанности вахтенного помощника. Подготовка к приему-высадке лоцмана.

Перед приемом-высадкой лоцмана вахтенный помощник капитана должен:

- отметить на карте предполагаемое место приема-высадки лоцмана, уточнить порядок связи с лоцманом;

- уточнить время подхода к точке приема-высадки лоцмана,

- дать с разрешения капитана указание вахтенному механику о переводе СЭУ в маневренный режим;

- сверить часы на мостике и в машинном отделении;

- подготовить и проверить средства сигнализации и связи;

- подготовить флаги "Голф", "Хотэл", а при входе в территориальные воды - национальный флаг страны порта захода и поднять его;

- подготовить якоря к отдаче, проверить связь с баком;

- включить вторую рулевую машину, если совместная работа двух рулевых машин технически возможна, перейти на ручное управление рулем;

- установить связь с лоцманской станцией, уточнить время подхода и место приема-высадки лоцмана, борт, с которого необходимо подать трап;

- подготовить с соответствии с требованиями ИМО и рекомендациями МАМЛ (приложение 10) лоцманский трап (подъемник), поручни, полутрапик, спасательный крут с линем и буйком, конец с карабином для подъема-спуска вещей лоцмана и проверить наличие освещения в ночное время лоцманского трапа (подъемника) и места приема-высадки лоцмана;

- предупредить капитана о подходе к месту приема-высадки лоцмана, поднять флаг "Голф" или другие сигналы, предписываемые местным правилам.

Прием-высадка лоцмана и работа с лоцманом.

При приеме-высадке лоцмана и в процессе лоцманской проводки судоводители должны:

- удостовериться в надежности крепления лоцманского трапа, поручней, полутрапика;

- вместе с вахтенным матросом встретить лоцмана и организовать прием его багажа;

- сопровождать лоцмана на мостик, представить лоцмана капитану, записать фамилию и инициалы лоцмана;

- спустить флаг "Голф", поднять флаг "Хотэл";

- выяснить у лоцмана, какие дополнительные флаги и сигналы необходимо поднять, и поднять их;

- обеспечить лоцмана информацией, необходимой для управления судном;

- получить у лоцмана информацию о соответствии используемой навигационной карты действительности, об условиях плавания в районе;

- дублировать команды лоцмана рулевому, контролировать правильность их выполнения;

- согласовать с лоцманом план швартовки и буксирного обеспечения, очередность подачи швартовных тросов и буксиров, после чего дать указание готовить буксирные тросы, если это требуется, и сообщить о борте швартовки на бак, корму и в машинное отделение;

- заполнить лоцманскую квитанцию;

- уточнить у лоцмана место его высадки, борт, с которого необходимо приготовить трап;

- обеспечить лоцману питание, обращая внимание на сервировку;

- провести лоцмана к трапу, лично убедиться в надежности его крепления, помочь лоцману спуститься.