Локсодромия и её свойства. Аналитические выражения для вычисления локсодромического курса и расстояния по географическим координатам. Меркаторская картографическая проекция, её свойства.

Кривую на поверхности Земли, пересекающую все мередианы под одним и тем же углом, называют локсодромией, что с греческого переводится как «косой бег».

Расстояние между двумя точками на сфере по локсодромии не является кратчайшим и её применение в мореплавании обьясняется исключительным удобством использования компасов.

Основные свойства локсодромии:

1. 
   Если К = 0 или 180⁰, то очевидно, что локсодромия совпадает с меридианом, то есть с большим кругом.
2. 
   Если К = 90⁰ или 270⁰, то локсодромия совпадает с параллелью или экватором, то есть образует малый или большой круг на поверхности сферы.
3. 
   При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.

Уравнение локсодромии для эллипсоида:

 

Более краткая запись выглядит так:
,

где V_1,2 – изометрическая широта.

Меркаторская проекция относится к классу цилиндрических нормальных равноугольных проекций, в которых параллели нормальной сетки есть параллельные прямые, а расстояние между меридианами пропорциональны соответствующим разностям долгот.

Основные этапы проектирования карты:

1-й этап: Осуществление геодезических измерений на поверхности Земли и их координатная привязка к конкретному референц-эллипсоиду.

 

2-й этап: Уменьшение размеров референц-эллипсоида до определённого масштаба с целью его дальнейшего развёртывания на плоскости, то есть создание условной эллипсоидальной модели Земли (глобуса) в масштабе, пригодном для изготовления карт. Это математическое преобразование эллипсоид – глобус сохраняет геометрическое подобие контуров изображений. Масштаб преобразования называется главным масштабом m_o будущей карты.

3-й этап: Выбор картографической проекции для развёртывания условного глобуса на плоскость и проектирование (преобразование глобус – карта). Из теории искажений известно, что при проектировании эллипсоида на плоскость масштаб m_o остаётся постоянным лишь на определённом множестве точек крты. В общем случае при удалении от этого множества масштаб изменяется и становится частным масштабом m другого множества точек. Величина называется увеличением масштаба.

Отношение частного масштаба к главному называется в картографии модулем параллели:

Меркаторской милей называется длина изображения одной минуты дуги меридиана D_ф в проекции меркатора, выраженная в линейных единицах в масштабе карты:

Линейный морской масштаб l_ф показывает, сколько морских миль содержится в одном сантиметре карты и представляет величину, обратную меркаторской миле:

Классификация карт, используемых в судовождении. Содержание карт. Руководства и пособия для плавания. Требования конвенции СОЛАС в отношении карт и пособий для плавания.

Морские карты и другие навигационные пособия на все районы океанов и морей издаются Главным управлением навигации и океанографии (ГУНиО), а в зарубежных странах – гидрографическими службами (департаментами).

Морские карты издаются главным образом в меркаторской проекции и по своему назначению подразделяются на три вида:

1. 
   Навигационные предназначаются для ведения счисления пути и определения места судна в море. К морским навигационым картам относятся общенавигационные, радионавигационные и т. д.
2. 
   Специальные предназначены для решения ряда задач судовождения при использовании особых технических средств. К специальным относятся рулонные и маршрутные карты и т. д.
3. 
   Вспомогательные и справочные морские карты, под названием которых объединены различные картографические издания ГУНиО. В эту группу входят: карты-сетки, карты в гномонической проекции для прокладки дуги большого круга, радиомаяков и радиостанций часовых поясов и т. д.

Общенавигационные карты являются основной подгруппой морских карт, обеспечивающих безопасность мореплавания. На них наиболее полно отражается рельеф дна, характер берегов и вся навигационная обстановка (огни, знаки, буи, фарватеры и др.).

В зависимости от масштаба общенавигационные марские карты подразделяются на: генеральные, имеющие масштаб от 1:1000000 до 1:5000000; путевые – от 1:100000; частные – от 1:25000 до 1:100000; планы – от 1:100 (при производстве различных гидрографических работ) до 1:25000.

Частные краты содержат все навигационные подробности. Дополнительно к картам издаются различные пособия и справочники, из которых можно почерпнуть много полезных, необходимых сведений. К таким пособиям можно отнести руководства для плавания (лоции), в которых собраны все необходимые для мореплавателя сведения, включая рекомендованные пути и советы по ориентировке при плавании вблизи берегов.

Для подбора карт и пособий издаётся специальный «Каталог карт и книг». Все карты и пособия имеют свой номер, который называется адмиралтейским.

Номера карт состоят из пяти цифр, которые означают: первая – океан или его часть (1 – Северный Ледовитый Океан, 2 и 3 – Северная и Южная часть Атлантики, 4 – Индийский Океан, 5 и 6 – Южная и Северная часть Тихого Океана), вторая – масштаб карты (каждой группе масштаб соответствует цифре от 0 до 4), третья – район моря, в пределах которой находится карта, четвёртая и пятая – порядковый номер в данном районе.

Навигационные морские карты и карты-сетки имеют номера, первой цифрой которой является 9. Вторая цифра обозначает океан или его часть; третья цифра – масштаб; последние две являются порядковыми номерами карты в океане.

 

6. Способность определения дрейфа судна. Учёт дрейфа и течения при счислении, точность счисления.

Дрейфом судна называется отклонение движущегося судна с линии намеченного курса под воздействием ветра и ветрового волнения. Направление ветра определяется по той точке горизонта, откуда дует ветер (ветер дует в компас) и выражается в румбах или градусах.

Дрейф возникает под воздействием силы давления набегающего потока воздуха на надводную часть судна. Скорость и направление этого потока соответствует вектору скорости кажущегося (наблюдаемого) ветра.

,где n - вектор скорости истинного ветра; V – вектор скорости судна; W – вектор скорости кажущегося ветра.

Несимметрические отклонения от курса под действием порывов ветра, ударов волн, отклонения руля вызывают зарыскивание судна, которое может быть как под ветер, так и на ветер.

Говоря об определении и учёте дрейфа, под термином «дрейф» будем понимать результирующее отклонение судна с линии истинного курса.

Полная сила А давления кажущегося ветра приложена к центру парусности надводной части судна и направлена под ветер.

В общем виде сила А определяется равенством:

, где C_q – коэффициент сопротивления надводной части судна.

Угол a между линией истинного курса и линией пути судна называется углом дрейфа.

Угол между северной частью истинного мередиана и линией пути при дрейфе называется путевым углом a.

,

Угол a имеет знак «+» - если ветер дует в левый борт, и «-» - если в правый.

Для учёта дрейфа при прокладке необходимо знать угол дрейфа, Угол дрейфа можно определить из наблюдений или вычислить по формулам, специально составленным таблицам или номограммам.

Учёт дрейфа при использования автоматического счисления координат сводится к введению дополнительной поправки курса, равной углу дрейфа судна. Для этого на приборе устанавливается поправка курса _DКл, равная алгебраической сумме поправки компаса и угла дрейфа:

 

7. Навигационная изолиния, линия положения, полоса положения. СКП определения места судна по двум линиям положения.

Геометрическое место точек, отвечающее постоянному значению навигационного параметра, называется навигационной изолинией. В навигации для определения места судна используются следующие навигационные параметры и соответствующие им изолинии:

 

Пеленг. На судне измерен истинный пеленг (ИП) предмета А, равный a. Проложив на карте линию пеленга АД, можно увтерждать, что судно в момент взятия пеленга находилось на этой линии. Прямая линия АД, отвечающая условию задачи, на которой находилось судно в момент наблюдения, будет называться изолинией пеленга или изопеленгой.

Расстояние. Измерено расстояние Д между судном и ориентиром А. В этом случае судно будет находится на окружности радиусом Д с центром в точке А. Эта окружность будет называться изолинией расстояния или изостадией.

Горизонтальный угол. Если измерен горизонтальный угол между предметами А и Б, равный a, или этот угол вычислен как разность двух пеленгов . Эта окружность называется изолинией горизонтального угла или изогоной.

Разность расстояний. В некоторых радионавигационных системах измеряется разность расстояний до двух ориентиров. Тогда изолинией разности расстояний будет гипербола.

Обобщённая теория линий пложения позволила расширить метода получения обсервованных кординат, которые можно подразделить на три группы: графические (использование карт с сетками изоолиний и непосредственная прокладка изолиний), графо-аналитические (обобщённый метод линий положения и использования специальных таблиц определяющих точек для построения линий положения), аналитический (прямые алгебраические методы решения уравнений и вычисления с использованием метода хорд или касательных).

При воздействии случайных ошибок измерений смещение каждой линии положения характеризуется линейной величиной _Dn, которое характеризуется линейной ошибкой линии положения m_Dn, а ошибка определения места, являющаяся результатом случайных ошибок в обеих линиях положения, характеризуется площадью параллелограмма, образованным двумя параметрами m_Dn₁ и m_Dn₂.

Общий порядок вычисления параллелограмма паогрешности обсервации судна при действии случайных ошибок таков:

Задаются средними квадратическими ошибками измерений для конкретных условий плавания m_v1 и m_v2.

Вычисляют возможное смещение каждой линии положения ; ; ; .

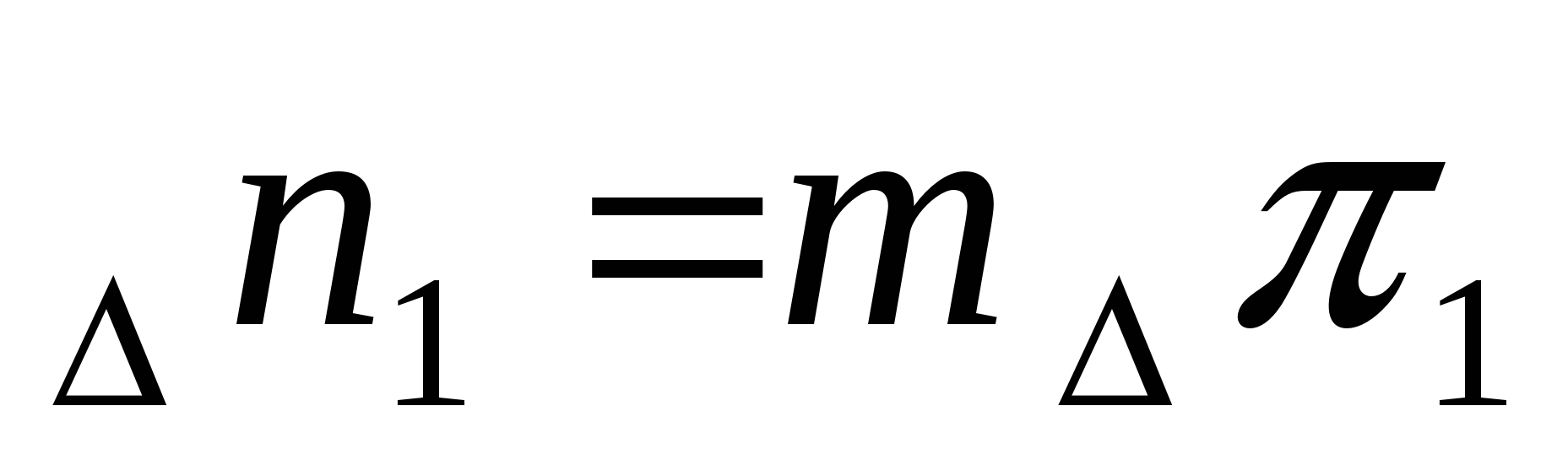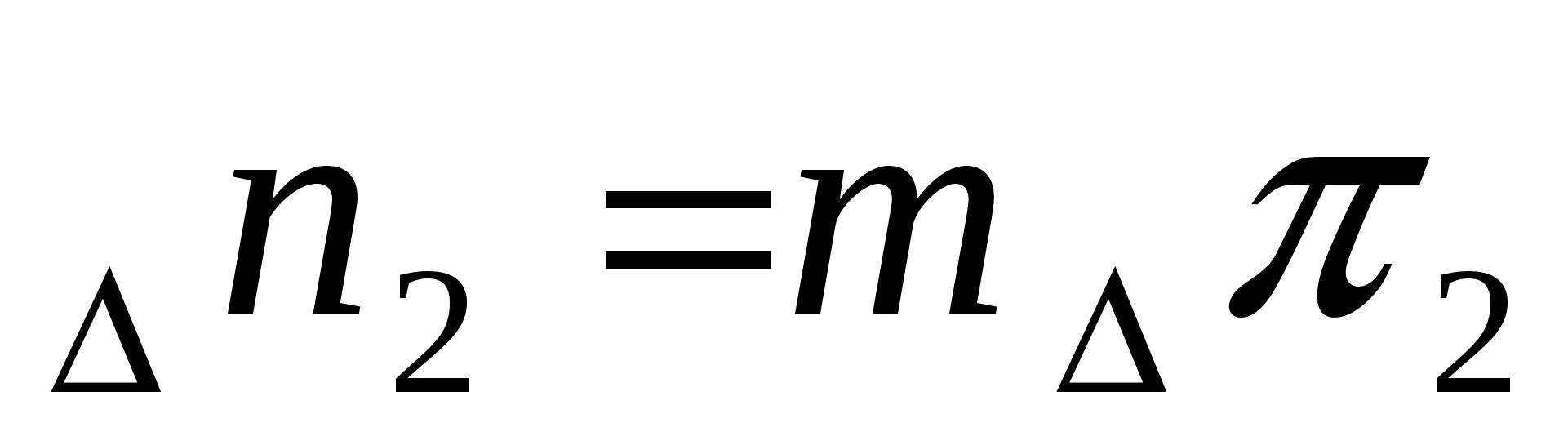Откладывают от полученнной обсервации по нормали к линии положения (по направлению градиентов) полученные смещения и строят параллелограмм abcd. Вероятность нахождения судна в площади параллелограмма около 50%; если взять для расчёта 2m, то вероятность увеличивается до 95%, а если принять предельную ошибку 3m, то вероятность повышается до 99%.

Для удобства анализа точность обсервации места судна целесообразнее оценить не площадью, а одним числом. За среднюю квадратическую ошибку обсервованного места М принимают радиус круга, охватывающий эллипс погрешности. Этот радиус равен:

. Вероятность того, что место судна находится внутри радиуса круга М изменяется от 63,2 до 68,3% и зависит от соотношения полуосей a и b.

8. Идея определения места судна по измерениям навигационных параметров. Способы определения места судна.

Определение места по двум пеленгам:

Способ определения места судна по двум пеленгам один из наиболее распространённых при плавании в узкостях или вдоль берега, вблизи навигационных опасностей.

Это объясняется ещё и тем, что часто в видимости судна не бывает одновременно большого количества ориентиров. Сущность способа состоит в следующем. В быстрой последовательности берут пеленги двух объектов (маяков, знаков, мысов и т. д.) Рассчитывают истинные пеленги, если имеется поправка компаса, и прокладывают их на карте.

В точке пересечения пеленгов будет обсервованное место судна F.

 

A Δ B Δ

Θ

 

F

Этот способ имеет ряд преимуществ (простота и быстрота определения), но и ряд недостатков, главным из которых является полное отсутствие контроля при единичном определении.

 

Величину линейной ошибки обсервованного места можно получить по формуле для систематической ошибки e_k град, подставляя в неё значения градиентов:

;; и град получим:

,

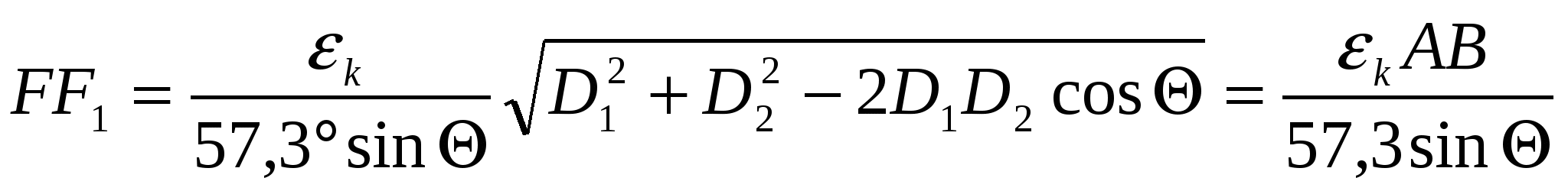где AB – расстояние между ориентирами.

Из этой формулы видно, что величина FF₁ будет увеличиваться с уменьшением Q (при постоянном AB и e_k). Поэтому при 30^о>Q>150^o, когда sinQ уменьшается особенно быстро, определение места по двум пеленгам нельзя считать точным.

Влияние случайных ошибок пеленгования.

Пеленгованию, как и любому измерению, сопутствуют случайные ошибки, к которым можно отнести ошибки из-за неточности наведения, колебаний в момент качки, отсутствие стабилизации в вертикальной плоскости и др. Это приводит к тому, что любому измеренному пеленгу соответствует ошибка , град. Если такую ошибку подставить в формулу для оценки точности обсервованного места, то получим формулу для средней квадратической погрешности обсервации по двум пеленгам:
.

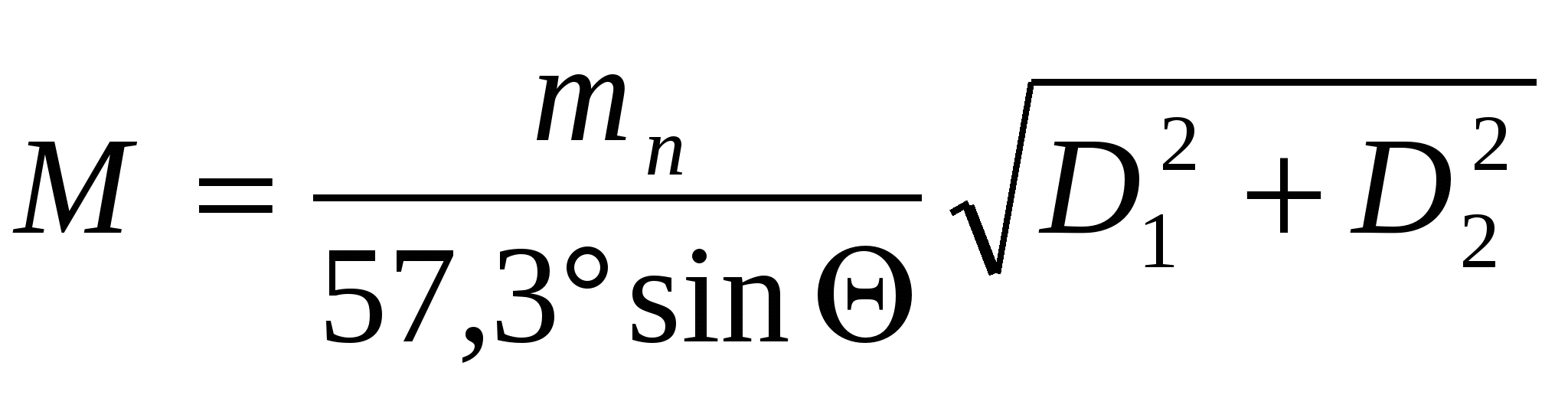Формула показывает, что при малых и близких к 180^о углах Q ошибки увеличиваются. Следовательно, место будет получаться точнее при Q=90 ^о. Точность определения зависит также от расстояния до ориентиров.

При определении места судна по двум пеленгам ошибка в принятой поправке компаса может быть значительно более случайных ошибок.

Для определения правильного значения поправки компаса по пеленгам двух предметов достаточно найти величину её ошибки, а затем алгебраически вычесть эту ошибку из принятого

значения поправки компаса: , где DК – поправка компаса, DКпр – принятое значение поправки компаса, e_к – ошибка принятого значения с её знаком.

 

Определение места по трём пеленгам.

При определении места по трём пеленгам в быстрой последовательности берут пеленга трёх предметов A, B, C. Переводят их в истинные и прокладывают на карте. Если бы наблюдения не содержали ошибок и пеленги были взяты одновременно, то все три пеленга пересеклись бы в одной точке F, представляющей собой место судна.

Однако из-за неизбежного действия ряда факторов пеленги обычно не пересекаются в одной точке, а образуют так называемый треугольник погрешности. Его появление может быть вызвано различными видами ошибок:

• 
  Промахами при снятии счёта и при исправлении компасных пеленгов;
• 
  Ошибки в опознавании ориентиров;
• 
  Ошибки в принятой поправке компаса;
• 
  Случайные ошибки пеленгования в прокладке.

Чтобы избежать графических ошибок при построении, можно рассчитать параллельное смещение каждой линии положения при изменении поправки на 3…5^о и построить новый треугольник погрешности, перенеся все линии положения в сторону увеличения или уменьшения. Для рассчёта смещения необходимо снять с карты расстояния до каждого из трёх предметов. Тогда:

, , .

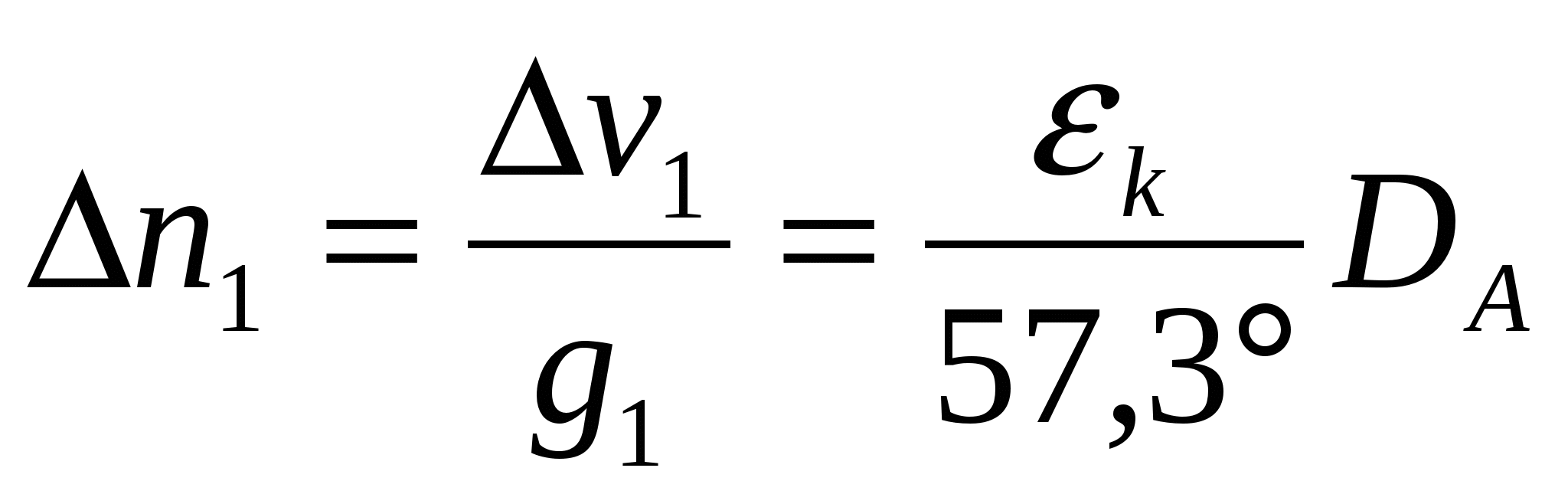Влияние ошибки, вызванной неодновременным взятием пеленгов, можно исключить несколькими способами. Один из них – правильный выбор очерёдности взятия пеленгов. Первым можно пеленговать объекты, расположенные ближе к диаметральной плоскости судна. Пеленги этих ориентиров изменяются медленнее. Если берутся пеленги огней маяков, то наблюдение надо так организовывать, чтобы не пришлось долго ждать проблеска огня, если он пеленгуется не первым. При скорости до 15 уз, когда прокладка ведётся на путевых картах, этого достаточно для исключения ошибки от неодновременного пеленгования. При больших скоростях или при ведении прокладки на крупномасштабных картах или планах для уточнения следует привести пеленга к среднему моменту. Для этого берут пять пеленгов в следующем порядке, пеленгуют ориентиры A, B и C, а затем ещё повторно пеленги В и А в обратном порядке. Считая, что пеленги изменяются линейно, рассчитывают среднее значение пеленгов объектов А и В.

 

, .

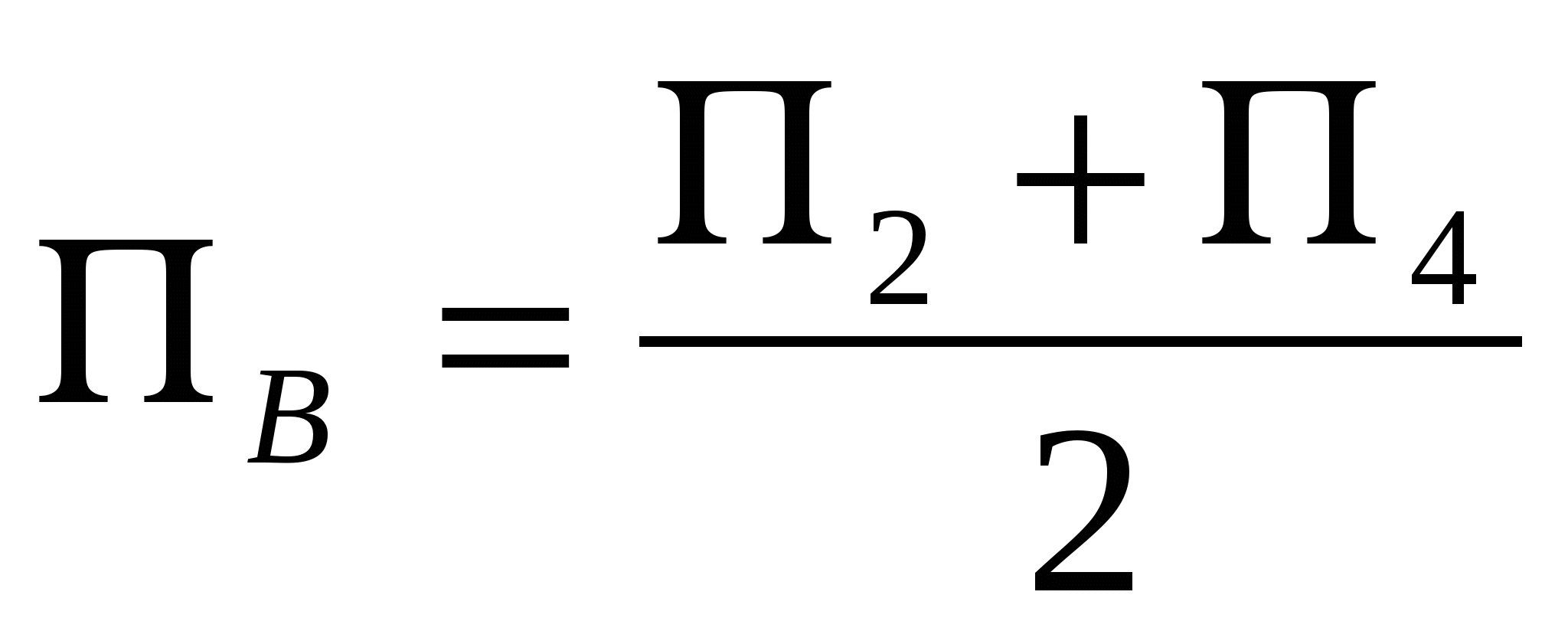Поправкой компаса называется величина параметра (курса или пеленга), компенсирующая систематическую ошибку его измерения. В общем виде поправка – это систематическая ошибка, взятая с обратным знаком.

Постоянную поправку гирокомпаса DГК по каждому ориентиру определяют как разность истинного и среднего измеренного пеленгов:

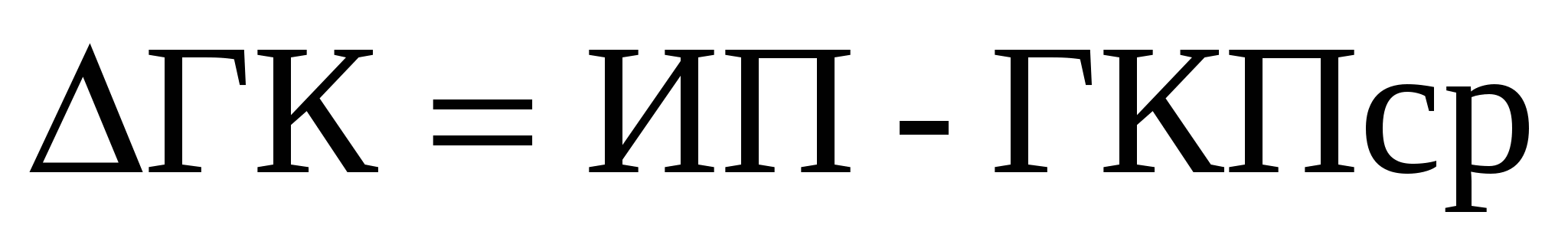
Определение расстояний в море.

Расстояние в море можно определить несколькими методами: с использованием дальномеров, по вертикальному углу, измеренным секстаном, по данным РЛС и глазомером.

Дальномеры представляют собой оптические приборы, измеряющие расстояния до видимого предмета на основе различных принципов.

Определение места судна по измеренным расстояниям.

Если в видимости судна имеются два ориентира, до которых измерены расстояния (по вертикальному углу или по данным РЛС), то обсервованные места судна можно получить по двум расстояниям. Пусть А и В – два объекта, до которых ичмерены расстояния ДА и ДВ. Известно, что измеренному расстоянию соответствует изолиния –окружность радиусом, равным этому расстоянию, и с центром в точке расположения ориентиров. Если оба наблюдения сделаны одновременно, то, проложив две окружности, в одной из точек получим место судна. Вопрос о том, какую из двух точек считать обсервованным местом, легко решается путём сопоставления её со счислимым местом.

Средняя квадратическая погрешность обсервации места по двум расстояниям получается, если в общую формулу подставить значения ошибок линий полодения, помня, что градиент расстояния равен единице.

.

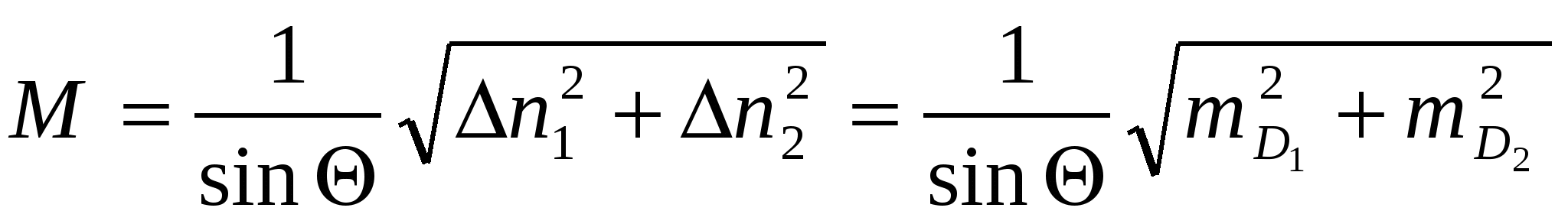Определение места судна по пеленгу и расстоянию.

Этот способ наиболее часто употребляется при использовании радиолокатора. Обычно пеленг и расстояние измеряют до одного ориентира, однако бывает целесообразнее измерить пеленг на светящийся маяк по компасу, а расстояние измерить до берега. В первом случае угол пересечения линий положения будет равен 90^о, а во втором – разности пеленгов, снятых с карты. Расстояние может быть измерено с помощью секстана по вертикальному углу либо получено приближённо по открытии маяка или глазомерно, при плавании по фарватеру или в узкостях.

Чтобы уменьшить ошибки неодновременности наблюдений, вначале измеряются расстояния, а затем берётся пеленг при положении предмета ближе к траверзу и в обратной последовательности – при острых углах. Обсервованное место получается на линии ИП на расстоянии от предмета, равном Д.

При измерении пеленга и расстояния до одного ориентира средняя квадратическая погрешность места судна равна (угол )

При измерении пеленга и расстояния до разных объектов требуется знать угол пересечения, тогда:

9. Градиенты навигационных параметров. Способы оцеки точности места судна при навигационных определениях. СКП и 95% погрешность в месте судна. Практический учёт погрешностей в определении места судна для безопасной навигации. Требования ИМО.

Любые измерения содержат ошибки, поэтому, измерив пеленг, дистанцию или угол и рположив на карте соответствующую изолинию, нельзя считать, что судно будет находиться на этой изолинии. Вычислить возможное смещение изолинии из-за ошибок можно, используя понятие градиента функции.

Вектор 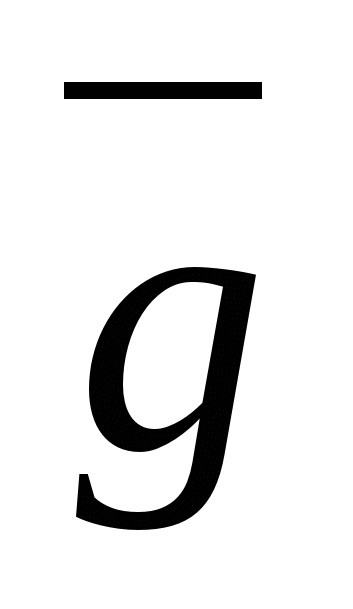называется градиентом – это вектор, направленный по нормали к навигационной изолинии в сторону её смещения при положительном приращении параметра, причём модуль этого вектора характеризует наибольшую скорость изменения параметра в данном месте. Этот модуль равен:

.

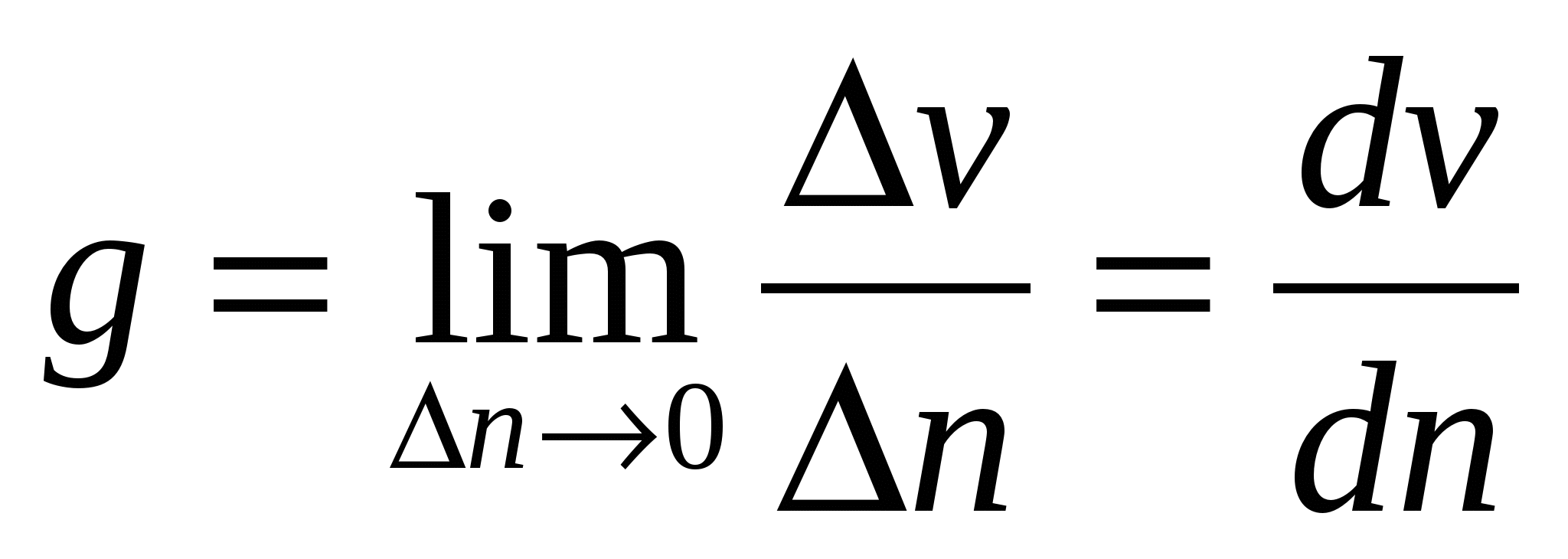Если при измерении навигационнаго параметра v допущена ошибка Dv и известен градиент, то смещение линии положения параллельно самой себе и определяется формулой:

.

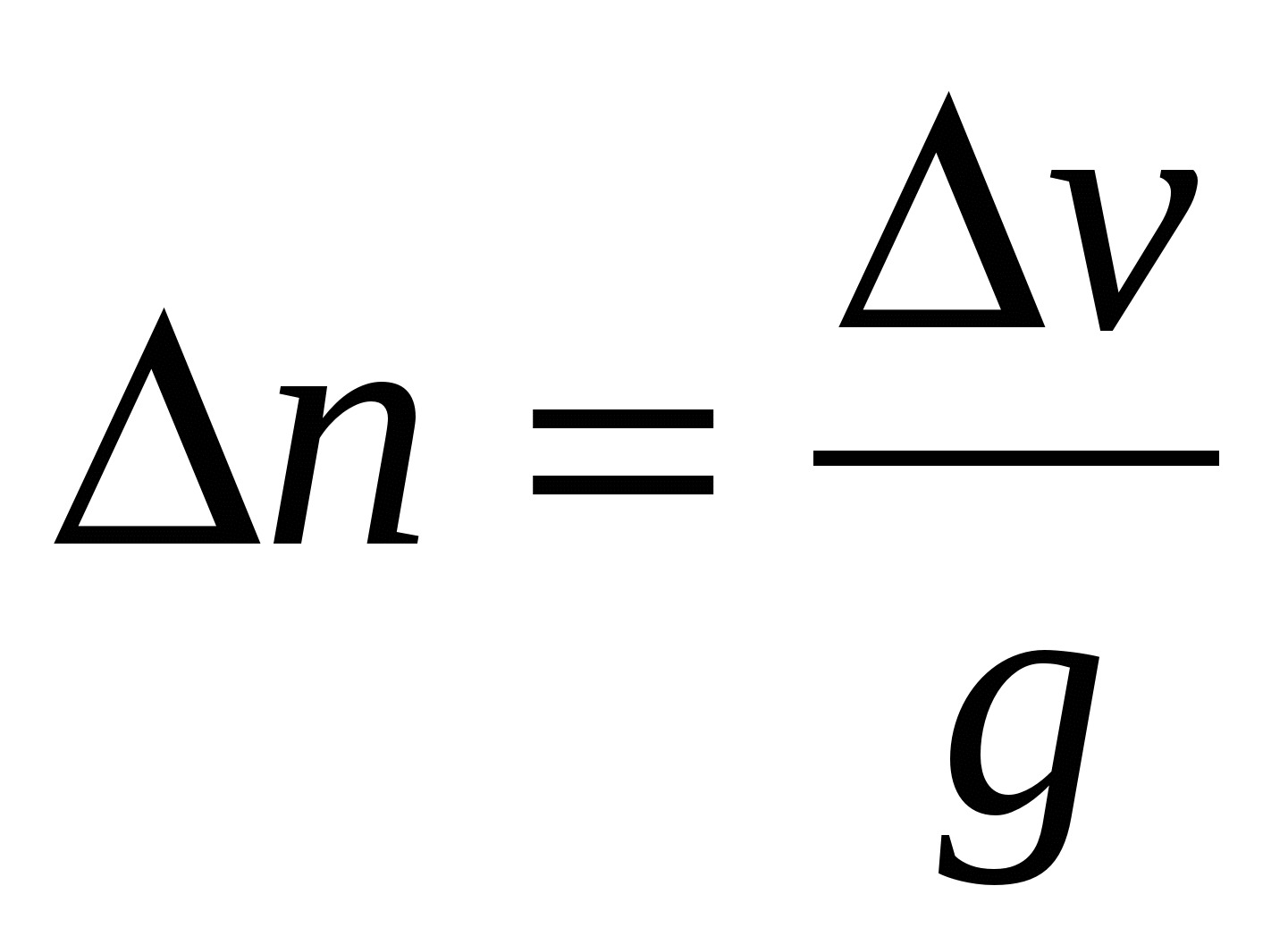Чем больше величина градиента g, тем меньше смещение линии положения при той же ошибке Dv, тем точнее будет определение места судна.

Если при измерении навигационного параметра имела место случайная погрешность m_П, град, то погрешность линии положения найдётся по формуле:

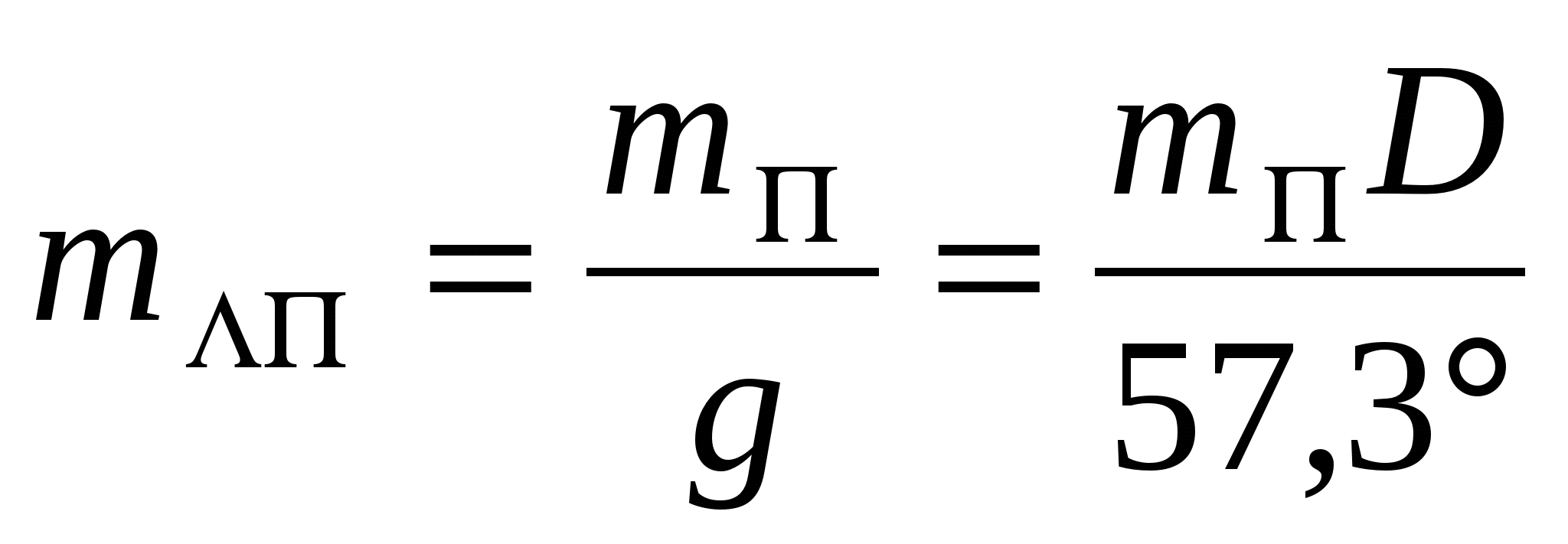.Полоса положения, ширина которой в три раза больше средней, захватывает места судна с вероятностью 99,7%. Такую полосу называют предельной полосой положения. Аналитически вычисляется по формуле: , где d –вспомогательный угол.

Значение угла d получается вычислением:

.

Смещение линии положения в милях равно:
,

где m’a - погрешность угла в дуговых минутах.

Для предотвращения навигационных аварий, связанных с посадкой на мель, наряду с другими мероприятиями предпринимались попытки нормировать требования к точности и частоте обсервации в зависимости от условий плавания. Неоднократное обсуждение этих вопросов в комитете по безопасности мореплавания Международной морской организации (ИМО) привело к созданию стандарта точности судовождения, принятому в 1983 г. на 13-й Ассамблее ИМО в резолюции А.529.

Цель принятого стандарта обеспечение руководства различного рода администраций стандартами точности судовождения, которые должны применяться при оценке эффективности работы систем,предназначенных для определения места судна, в том числе радионавигационных систем, включая спутниковые. От судоводителя требуется знать свое место на любой момент времени. В стандарте указаны факторы, влияющие на требования к точности судовождения. К ним относятся:

скорость судна, расстояние до ближайшей навигационной опасности, которой считается всякий признанный или нанесённый на карту элемент, граница района плавания.

При плавании в других водах со скоростью до 30 узлов текущее место судна должно быть известно с погрешностью не более 4% расстояния до ближайшей опасности. При этом точность места должна оцениваться фигурой погрешностей с учётом случайных и систематических ошибок с вероятностью 95%. В стандарт ИМО включена таблица, которая содержит требования к точности места, а также допустимое время плавания по счислению при условии, что гирокомпас и лаг (время плавания), соответствуют требованиям ИМО, счисление не корректировалось, погрешности имеют нормальное распределение, а течение и дрейф учитываются с возможной точностью.

 

10. Ортодромия, ортодромическая поправка. Способы построения ортодромии на картах меркаторской проекции.
Ортодромическая поправка

При определении ИРП измеряют угол между истинным меридианом и дугой большого круга, по которой распространяется радиоволна от источника ее излучения М до места приема К на сфере (рис. 13.4). Измеренный угол является ортодромическим пеленгом.

Если на меркаторской проекции от места радиомаяка АД отложить, как это обычно делается, линию обратного ИРП (ОИРП) то место судна получится не в направлении МК, а в направлении MKi.

Для того чтобы линия пеленга, проложенная на меркаторской карте, прошла через место судна К, измеренный оргодромический пеленг должен быть переведен в локсодромический пеленг (Лок П) путем прибавления к нему угла y, называемого оргодромической поправкой:

Лок П = ИРП + y

Ортодромическая поправка является поправкой за кривизну изображения дуги большого круга на меркаторской карте. Найдем величину этой поправки по рис. 13.5, изображающему Северное полушарие Земли с проведенной на нем через точки К и М дугой большого круга. Эта дуга составляет с меридианами точек К и М соответственно углы Ai и Ад. Эти углы не равны между собой, так как дуга большого круга пересекает меридианы под разными углами.

Разность двух сферических углов, под которыми дуга большого круга пересекает меридианы двух заданных точек, назывется схождением меридианов. Величину схождения меридианов точек К и М можно найти, если применить к треугольнику КРМ аналогию Непера. На основании ее можно написать:

 

Из формулы (13.7) видно, что y не может быть больше РД. С увеличением широты схождение меридианов увеличивается. Наибольшего значения, равного 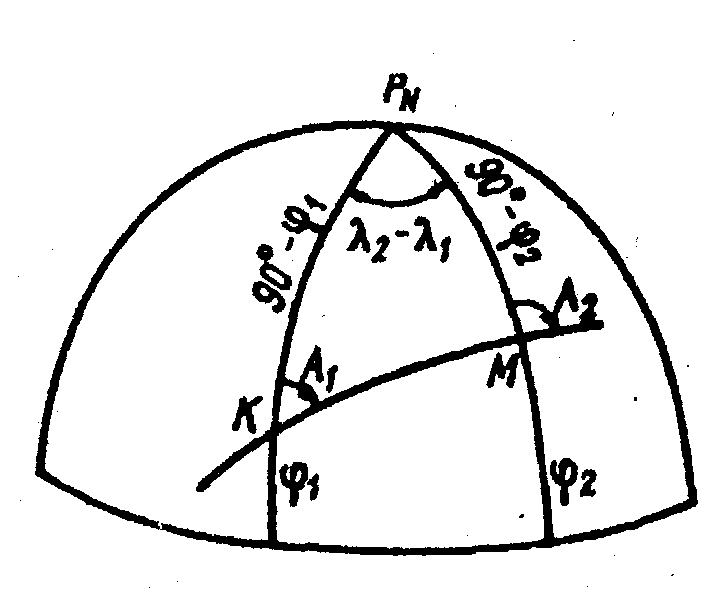разности долгот, схождение меридианов достигает при рт = 90°.

Значение оргодромической поправки можно найти по схождению меридианов на рис. 13.6, изображающем в меркаторской проекции часть земного шара с точками К и М, через которые проходит дуга большого круга, составляющая с меридианами данных точек углы Ai и Ад. На меркаторской проекции дуга большого круга изобразится кривой, обращенной своей выпуклостью к ближайшему полюсу. Локсодромия, проходящая через точки К и М, пересекает их меридианы под одним и тем же углом К.

Предположим, что расстояние между точками К и М сравнительно невелико, вследствие чего можно считать, что дуга большого круга, проходящая через эти точки, изображается дугой окружности. Это предположение будет верным с достаточной для практики точностью для расстояний до нескольких сотен миль. Тогда дуга большого круга будет составлять с локсодромией в точках К и М равные углы y.

Из рис. 13.6 видно, что в точке К поправка ip = К-Ац в точке М поправка гр = А; - К. Суммируя эти равенства, получаем


Формула эта является прибли­женной потому, что при выводе ее мы допустили равенство ортодромических поправок в точках К и М. В действительности оргодромические поправки в этих точках не равны.

Подставляя эти данные в формулу (13.8) получаем:

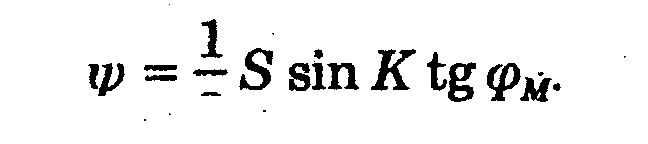
При решении различных задач навигации чаще всего приходится находить локсодромический пеленг в данной точке при известном ортодромическом пеленге. Эту задачу решают по алгебраической формуле (13.5).

Знак ортодромической поправки зависит от взаимного расположения судна и пеленгуемой им радиостанции и определяется по следующему правилу: если в Северном полушарии судно расположено к западу от радиостанции (величина пеленга в круговом счете от 0 до 180°), ортодромическая поправка имет знак «+»;если судно находится к востоку от радиостанции (величина пеленга от 180 до 360°), ортодромическая поправка имеет знак «-». В южном полушарии правило знаков будет обратным (рис. 13.7).

При выводе приближенной формулы ортодромической поправки было сделано предположение, что дуга большого круга изображается на меркаторской карте дугой окружности, вследствие чего ортодромическая поправка у обоих ее концов будет одинакова. Более строгое исследование, вопроса об ортодромической поправке показывает, что дуга большого круга на меркаторской карте изображается кривой, не являющейся окружностью, и ортодромическая поправка у разных концов дуги большого круга будет разной.

На больших расстояниях, когда DА > 10°, следует использовать точное значение ортодромической поправки. Точное значение орто­дромической поправки можно найти с помощью табл. 23-6 МТ-75, составленной по формуле:

A₁ —ортодромическое направление, определяемое из выражения (13.2).

Повысить точность нахождения ортодромической поправки (при (р > 35°), можно, пользуясь обычной таблицей, составленной по приближенной формуле (13.8). Входить в эту таблицу следует не со средней широтой, а с широтой точки, для которой находится ортодромическая поправка. Ортодромическую поправку следует учитывать во всех случаях, когда ее величина больше случайных погрешностей прокладки, (их обычно принимают равными ± 0,3°).