Теорема Ролля. Если функция  непрерывна,на отрезке
непрерывна,на отрезке  , и дифференцируема в промежутке
, и дифференцируема в промежутке  и принимает на концах отрезка
и принимает на концах отрезка  равные значения
равные значения 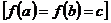 , то в промежутке
, то в промежутке  найдется по крайней мере одна такая точка
найдется по крайней мере одна такая точка  , в которой производная будет равна нулю:
, в которой производная будет равна нулю: 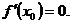
Теорема Коши. Если две функции  и
и 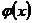 непрерывны на отрезке
непрерывны на отрезке  и дифференцируемы в промежутке
и дифференцируемы в промежутке  , причем производная второй из них
, причем производная второй из них  не обращается в нуль в этом промежутке, то отношение конечных приращений этих функций на отрезке
не обращается в нуль в этом промежутке, то отношение конечных приращений этих функций на отрезке  равно отношению их производных в некоторой точке с промежутка
равно отношению их производных в некоторой точке с промежутка  , быть может, не единственной:
, быть может, не единственной:  (5.7)
(5.7)
Заметим, что 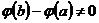 , так как иначе по теореме Ролля производная
, так как иначе по теореме Ролля производная  обращалась бы в нуль хотя бы в одной точке промежутка
обращалась бы в нуль хотя бы в одной точке промежутка  , а по условию теоремы Коши
, а по условию теоремы Коши  в этом промежутке.
в этом промежутке.
Доказательство. Введем вспомогательную функцию  , где
, где  — неопределенный пока постоянный множитель, и выберем
— неопределенный пока постоянный множитель, и выберем  так, чтобы функция
так, чтобы функция  удовлетворяла на отрезке
удовлетворяла на отрезке  всем условиям теоремы Ролля. Для этого нам достаточно потребовать, чтобы
всем условиям теоремы Ролля. Для этого нам достаточно потребовать, чтобы  , так как остальным условиям теоремы Ролля функция
, так как остальным условиям теоремы Ролля функция  удовлетворяет: она непрерывна на отрезке
удовлетворяет: она непрерывна на отрезке  и дифференцируема в промежутке
и дифференцируема в промежутке  , так как этими свойствами обладают обе функции
, так как этими свойствами обладают обе функции  и
и 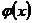 .
.
Итак, потребуем, чтобы  или чтобы
или чтобы 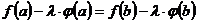 . Это дает для множителя
. Это дает для множителя  конечное значение:
конечное значение:
 (5.8) поскольку
(5.8) поскольку 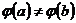 .
.
При таком значении  функция
функция  будет удовлетворять всем условиям теоремы Ролля. Поэтому ее производная
будет удовлетворять всем условиям теоремы Ролля. Поэтому ее производная 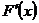 обратится в нуль по крайней мере в одной точке
обратится в нуль по крайней мере в одной точке  промежутка
промежутка  :
: 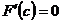 ; или, так как
; или, так как  , то
, то  . По условию теоремы
. По условию теоремы  [
[  в промежутке
в промежутке  ]. Поэтому из предыдущего равенства найдем
]. Поэтому из предыдущего равенства найдем 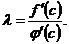 (5.9)
(5.9)
Сравнивая правые части равенств (5.8) и (5.9), определяющих одно и то же число  , получим равенство (14.7). Теорема Коши доказана.
, получим равенство (14.7). Теорема Коши доказана.
Теорему Лагранжа получим, положив  , в силу чего
, в силу чего 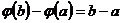 ,
,  и
и  .
.
Внося эти-значения в равенство (5.7), получаем  (5.10) или
(5.10) или  (5.11)
(5.11)
Полученная формула (5.11) называется формулой Лагранжа, и определяет содержание теоремы Лагранжа: конечное приращение на отрезке  функции, непрерывной на этом отрезке и дифференцируемой внутри него, равно произведению конечного приращения аргумента на этом отрезке на значение производной в некоторой внутренней точке отрезка
функции, непрерывной на этом отрезке и дифференцируемой внутри него, равно произведению конечного приращения аргумента на этом отрезке на значение производной в некоторой внутренней точке отрезка 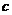 .
.
Геометрический смысл теоремы Лагранжа определяется формулой (5.10). В ней левая часть равна угловому коэффициенту уравнения хорды  , соединяющей точки
, соединяющей точки  и
и  графика функции
графика функции  (см. рис. 5.18):
(см. рис. 5.18):
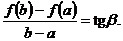

Правая часть этой формулы  равна угловому коэффициенту касательной к этому графику в точке
равна угловому коэффициенту касательной к этому графику в точке  с абсциссой
с абсциссой  , где
, где  (рис. 5.18):
(рис. 5.18):
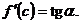
Формула (5.10) устанавливает равенство этих угловых коэффициентов, т. е. параллельность хорды и касательной. Таким образом, геометрический смысл теоремы Лагранжа следующий: На произвольной дуге графика дифференцируемой функции всегда найдется такая точка, в которой касательная к графику будет параллельна хорде, стягивающей концы дуги.
Тот же геометрический смысл имеет и теорема Коши, если рассматривать функции  и
и 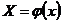 как параметрические уравнения некоторой кривой на плоскости
как параметрические уравнения некоторой кривой на плоскости 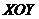 , а
, а  при этом считать параметром этой кривой.
при этом считать параметром этой кривой.
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида 
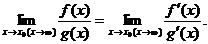 (1)
(1)
Доказательство.
Рассмотрим доказательство теоремы для неопределенности вида  при
при  . Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем
. Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем  и
и 
В этом случае 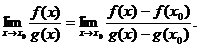
Применяя теорему Лагранжа для функций f(x) и g(x) на отрезке  , получим
, получим  где
где 
При  в силу непрерывности производных
в силу непрерывности производных  и
и  имеем
имеем 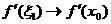 и
и 



 непрерывна,на отрезке
непрерывна,на отрезке  , и дифференцируема в промежутке
, и дифференцируема в промежутке  и принимает на концах отрезка
и принимает на концах отрезка 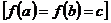 , то в промежутке
, то в промежутке  , в которой производная будет равна нулю:
, в которой производная будет равна нулю: 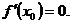
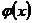 непрерывны на отрезке
непрерывны на отрезке  не обращается в нуль в этом промежутке, то отношение конечных приращений этих функций на отрезке
не обращается в нуль в этом промежутке, то отношение конечных приращений этих функций на отрезке  (5.7)
(5.7)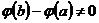 , так как иначе по теореме Ролля производная
, так как иначе по теореме Ролля производная  в этом промежутке.
в этом промежутке. , где
, где  — неопределенный пока постоянный множитель, и выберем
— неопределенный пока постоянный множитель, и выберем  удовлетворяла на отрезке
удовлетворяла на отрезке  , так как остальным условиям теоремы Ролля функция
, так как остальным условиям теоремы Ролля функция 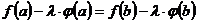 . Это дает для множителя
. Это дает для множителя  (5.8) поскольку
(5.8) поскольку 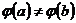 .
.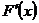 обратится в нуль по крайней мере в одной точке
обратится в нуль по крайней мере в одной точке  промежутка
промежутка 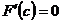 ; или, так как
; или, так как  , то
, то  . По условию теоремы
. По условию теоремы  [
[ 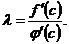 (5.9)
(5.9) , в силу чего
, в силу чего 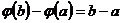 ,
,  и
и  .
. (5.10) или
(5.10) или  (5.11)
(5.11)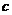 .
. , соединяющей точки
, соединяющей точки  и
и  графика функции
графика функции  (см. рис. 5.18):
(см. рис. 5.18):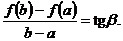

 равна угловому коэффициенту касательной к этому графику в точке
равна угловому коэффициенту касательной к этому графику в точке  с абсциссой
с абсциссой  (рис. 5.18):
(рис. 5.18):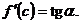
 и
и 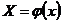 как параметрические уравнения некоторой кривой на плоскости
как параметрические уравнения некоторой кривой на плоскости 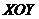 , а
, а  при этом считать параметром этой кривой.
при этом считать параметром этой кривой.
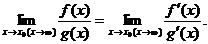 (1)
(1) при
при  . Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем
. Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем  и
и 
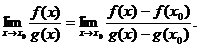
 , получим
, получим  где
где 
 и
и  имеем
имеем 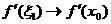 и
и 


