Раскрытием неопределенности в математическом анализе называют отыскание предела 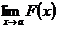 , когда функция
, когда функция  непрерывна вблизи точки
непрерывна вблизи точки  , но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения
, но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения  приводит к выражению неопределенного вида:
приводит к выражению неопределенного вида:

[Подобная же задача возникает и при отыскании 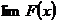 .]
.]
Теперь, опираясь на теорему Коши, выведем правило Бернулли — Лопиталя для раскрытия неопределенностей, использующее производные.
Основными видами неопределенностей являются два: 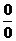 и
и  .
.
Раскрытие этих неопределенностей означает вычисление предела отношения двух бесконечно малых и предела отношения двух бесконечно больших. Для этих двух видов неопределенностей и будет выведено сейчас правило Бернулли — Лопиталя. Вывод правила разбивается на 4 случая. Первые два посвящены отношению двух бесконечно малых (при  и при
и при  ); вторые два - отношению двух бесконечно больших (при
); вторые два - отношению двух бесконечно больших (при  и при
и при  ).
).
Остальные виды неопределенностей, как увидим дальше, приводятся к основным двум видам: 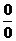 и
и  .
.
I случай. Неопределенность вида 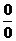 (при
(при  ). Пусть требуется найти
). Пусть требуется найти  , когда
, когда 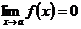 и
и  .
.
Примем  ; тогда функции
; тогда функции 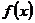 и
и 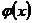 будут непрерывными в точке
будут непрерывными в точке  .
.
Предположим, что обе функции 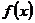 и
и 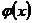 дифференцируемы вблизи точки
дифференцируемы вблизи точки  , причем
, причем  . Докажем при этих условиях, что если существует конечный или бесконечный предел отношения производных
. Докажем при этих условиях, что если существует конечный или бесконечный предел отношения производных
 , то
, то 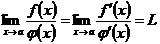 , т. е. что искомый предел отношения функций в этом случае также существует и равен пределу отношения производных.
, т. е. что искомый предел отношения функций в этом случае также существует и равен пределу отношения производных.
Для доказательства применим к функциям 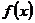 и
и 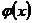 на некотором отрезке
на некотором отрезке 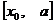 теорему Коши, выбрав за
теорему Коши, выбрав за  произвольное значение
произвольное значение  , принадлежащее той окрестности точки
, принадлежащее той окрестности точки  , в которой обе функции будут непрерывны и, кроме того, дифференцируемы вблизи точки
, в которой обе функции будут непрерывны и, кроме того, дифференцируемы вблизи точки  , т. е. во всех точках этой окрестности, кроме, может быть, самой точки
, т. е. во всех точках этой окрестности, кроме, может быть, самой точки  . Получаем
. Получаем

Это равенство, в силу того что  , приводится к виду
, приводится к виду
 где
где  ; если теперь устремить
; если теперь устремить  к
к  , то одновременно и
, то одновременно и 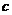 будет стремиться к
будет стремиться к  ; поэтому
; поэтому
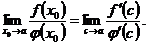
В этом предельном равенстве ничто не изменится, если  и
и 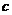 заменить просто символом
заменить просто символом  :
:
 (5.12)
(5.12)
В самом деле,  есть произвольное, достаточно близкое к
есть произвольное, достаточно близкое к  значение аргумента
значение аргумента  . Поэтому можно символ
. Поэтому можно символ  заменить просто символом
заменить просто символом  в левой части предельного равенства. Далее, по условию существует
в левой части предельного равенства. Далее, по условию существует
 при произвольном способе стремления
при произвольном способе стремления  к
к  ; значит, существует и равен ему
; значит, существует и равен ему  . Поэтому можно в правой части предельного равенства заменять
. Поэтому можно в правой части предельного равенства заменять  на
на  .
.
Тот же результат получим, если вместо отрезка 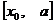 , рассмотрим отрезок
, рассмотрим отрезок 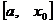 . Равенство (14.12) и дает нам правило Бернулли — Лопиталя для рассматриваемого нами случая.
. Равенство (14.12) и дает нам правило Бернулли — Лопиталя для рассматриваемого нами случая.
II случай. Неопределенность вида 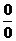 (при
(при  ). Докажем, что правило (5.12) остается в силе и в случае, когда
). Докажем, что правило (5.12) остается в силе и в случае, когда  .
.
Пусть требуется найти  , если
, если  .
.
Предположим, что при всех достаточно больших по абсолютной величине значениях  (т. е. при
(т. е. при  ,
,  ) обе функции дифференцируемы и
) обе функции дифференцируемы и  и что существует (конечный или бесконечный)
и что существует (конечный или бесконечный) 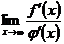 . Докажем, что тогда
. Докажем, что тогда  .
.
Для доказательства перейдем к новому аргументу, положив 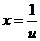 ; при
; при  , и
, и 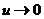 .
.
Легко видеть, что к отношению  правило (5.12) применимо: в окрестности точки
правило (5.12) применимо: в окрестности точки  обе функции дифференцируемы, производная
обе функции дифференцируемы, производная  и существует
и существует  .
.
Но тогда, применяя правило (5.12), получим  .
.
Возвращаясь к аргументу  , находим то, что было необходимо. Это же правило сохраняется и в том случае, когда аргумент стремится к бесконечности только по положительным или только по отрицательным значениям, т. е. когда
, находим то, что было необходимо. Это же правило сохраняется и в том случае, когда аргумент стремится к бесконечности только по положительным или только по отрицательным значениям, т. е. когда  или
или  .
.
III случай. Неопределенность вида  (при
(при  ). Пусть теперь требуется найти
). Пусть теперь требуется найти  , если
, если  .
.
Пусть и в этом случае будут соблюдены условия, оговоренные нами при рассмотрении I случая, т. е. пусть вблизи точки  обе функции
обе функции 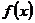 и
и 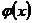 дифференцируемы и
дифференцируемы и  . Докажем тогда, что если существует (конечный или бесконечный)
. Докажем тогда, что если существует (конечный или бесконечный)  , то правило Бернулли— Лопиталя (512) остается в силе, т. е.
, то правило Бернулли— Лопиталя (512) остается в силе, т. е.  .
.
Для доказательства возьмем в окрестности точки  два значения
два значения  :
: 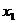 и
и 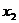 , причем пусть
, причем пусть  , если точки
, если точки 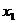 и
и 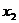 берутся слева от
берутся слева от  , и
, и  , если берутся справа от
, если берутся справа от  . Тогда на отрезке
. Тогда на отрезке  (или
(или  к отношению функций
к отношению функций 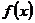 и
и 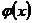 применима теорема Коши:
применима теорема Коши:
 , (5.14) где
, (5.14) где  (или
(или 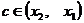 ).
).
Разберем сначала случай, когда существует конечный предел отношения производных:
 .
.
Задав произвольно малое положительное число  , определим
, определим  так, чтобы при
так, чтобы при  выполнялось неравенство
выполнялось неравенство
 . (5.15)
. (5.15)
Выберем теперь 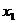 так, чтобы
так, чтобы  и фиксируем его значение; тогда, согласно условию выбора
и фиксируем его значение; тогда, согласно условию выбора 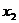 , для всякого выбранного
, для всякого выбранного 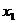 будем иметь и подавно
будем иметь и подавно  и
и  , поскольку
, поскольку 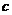 заключено между
заключено между 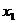 и
и 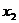 . Поэтому в силу неравенства (5.15) будем иметь
. Поэтому в силу неравенства (5.15) будем иметь
 , или
, или  .
.
Заменяя в этом неравенстве, согласно (14.14), отношение 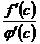 равным ему отношением
равным ему отношением
 , находим
, находим 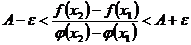 . (5.16)
. (5.16)
Преобразуем это неравенство следующим образом:  .(5.17)
.(5.17)
Если теперь устремить 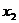 к
к  , не изменяя
, не изменяя 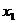 , то в силу условий
, то в силу условий  будем иметь
будем иметь
 .
.
Поэтому при заданном  найдется таксе
найдется таксе  , что при
, что при  , будет выполняться неравенство:
, будет выполняться неравенство:
 , или
, или  .
.
Перемножая теперь почленно неравенства (517) и (5.18), что возможно, поскольку члены неравенства (5.18) положительны, получаем 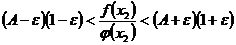 .(5.19)
.(5.19)
Но  ,
,  ; следовательно, неравенство (5.19) показывает, что при выбранных значениях
; следовательно, неравенство (5.19) показывает, что при выбранных значениях 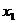 и
и 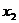 разность между переменной величиной
разность между переменной величиной  и постоянной
и постоянной  будет величиной бесконечно малой.
будет величиной бесконечно малой.
Поэтому  и, следовательно,
и, следовательно,  . (5.20)
. (5.20)
Если же  , то, во-первых, тогда
, то, во-первых, тогда  в достаточно малой окрестности точки
в достаточно малой окрестности точки  (иначе, отношение
(иначе, отношение  было бы бесконечно большим), во-вторых,
было бы бесконечно большим), во-вторых,  (поскольку величина, обратная к бесконечно большой, бесконечно мала), а потому к обратному отношению
(поскольку величина, обратная к бесконечно большой, бесконечно мала), а потому к обратному отношению  применимо предыдущее правило, следовательно,
применимо предыдущее правило, следовательно,
 , откуда следует справедливость и формулы (5.20).
, откуда следует справедливость и формулы (5.20).
IV Случай. Неопределенность вида  (при
(при  ). Правило (5.20) сохраняется и при
). Правило (5.20) сохраняется и при  :
:
 (5.21) при условии, что
(5.21) при условии, что  и что обе функции
и что обе функции  и
и  дифференцируемы при всех достаточно больших по абсолютной величине значениях
дифференцируемы при всех достаточно больших по абсолютной величине значениях  (
( ,
,  ), причем
), причем  , и при условии, что существует (конечный или бесконечный)
, и при условии, что существует (конечный или бесконечный) 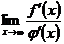 .
.



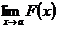 , когда функция
, когда функция  непрерывна вблизи точки
непрерывна вблизи точки  , но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения
, но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения 
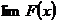 .]
.]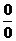 и
и  .
. и при
и при  ); вторые два - отношению двух бесконечно больших (при
); вторые два - отношению двух бесконечно больших (при  , когда
, когда 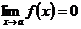 и
и  .
. ; тогда функции
; тогда функции 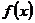 и
и 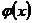 будут непрерывными в точке
будут непрерывными в точке  , причем
, причем  . Докажем при этих условиях, что если существует конечный или бесконечный предел отношения производных
. Докажем при этих условиях, что если существует конечный или бесконечный предел отношения производных , то
, то 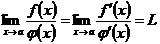 , т. е. что искомый предел отношения функций в этом случае также существует и равен пределу отношения производных.
, т. е. что искомый предел отношения функций в этом случае также существует и равен пределу отношения производных.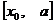 теорему Коши, выбрав за
теорему Коши, выбрав за  произвольное значение
произвольное значение  , принадлежащее той окрестности точки
, принадлежащее той окрестности точки 
 где
где  ; если теперь устремить
; если теперь устремить  будет стремиться к
будет стремиться к 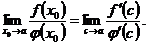
 (5.12)
(5.12) при произвольном способе стремления
при произвольном способе стремления  . Поэтому можно в правой части предельного равенства заменять
. Поэтому можно в правой части предельного равенства заменять  .
.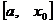 . Равенство (14.12) и дает нам правило Бернулли — Лопиталя для рассматриваемого нами случая.
. Равенство (14.12) и дает нам правило Бернулли — Лопиталя для рассматриваемого нами случая. .
. , если
, если  .
. ,
,  ) обе функции дифференцируемы и
) обе функции дифференцируемы и 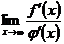 . Докажем, что тогда
. Докажем, что тогда  .
.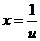 ; при
; при 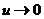 .
. правило (5.12) применимо: в окрестности точки
правило (5.12) применимо: в окрестности точки  обе функции дифференцируемы, производная
обе функции дифференцируемы, производная  и существует
и существует  .
. .
. или
или  .
. .
. , то правило Бернулли— Лопиталя (512) остается в силе, т. е.
, то правило Бернулли— Лопиталя (512) остается в силе, т. е.  .
.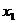 и
и 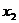 , причем пусть
, причем пусть  , если точки
, если точки  , если берутся справа от
, если берутся справа от  (или
(или  к отношению функций
к отношению функций  , (5.14) где
, (5.14) где  (или
(или 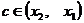 ).
). .
. , определим
, определим  так, чтобы при
так, чтобы при  выполнялось неравенство
выполнялось неравенство . (5.15)
. (5.15) и фиксируем его значение; тогда, согласно условию выбора
и фиксируем его значение; тогда, согласно условию выбора  и
и  , поскольку
, поскольку  .
.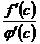 равным ему отношением
равным ему отношением , находим
, находим 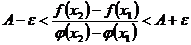 . (5.16)
. (5.16) .(5.17)
.(5.17) .
. , что при
, что при  , будет выполняться неравенство:
, будет выполняться неравенство: , или
, или  .
.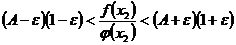 .(5.19)
.(5.19) ,
,  ; следовательно, неравенство (5.19) показывает, что при выбранных значениях
; следовательно, неравенство (5.19) показывает, что при выбранных значениях  и постоянной
и постоянной  будет величиной бесконечно малой.
будет величиной бесконечно малой. и, следовательно,
и, следовательно,  . (5.20)
. (5.20) , то, во-первых, тогда
, то, во-первых, тогда  было бы бесконечно большим), во-вторых,
было бы бесконечно большим), во-вторых,  (поскольку величина, обратная к бесконечно большой, бесконечно мала), а потому к обратному отношению
(поскольку величина, обратная к бесконечно большой, бесконечно мала), а потому к обратному отношению  применимо предыдущее правило, следовательно,
применимо предыдущее правило, следовательно, , откуда следует справедливость и формулы (5.20).
, откуда следует справедливость и формулы (5.20). (5.21) при условии, что
(5.21) при условии, что  и что обе функции
и что обе функции  и
и  дифференцируемы при всех достаточно больших по абсолютной величине значениях
дифференцируемы при всех достаточно больших по абсолютной величине значениях 


