Для описания динамики аналоговых или непрерывных систем используются дифференциальные уравнения. В дискретных же системах передача информации осуществляется с помощью дискретных сигналов, которые можно рассматривать как последовательности чисел, иногда называемые решетчатыми функциями. Решетчатые функции являются аналогами непрерывных функций, описывающих непрерывные системы.
Решетчатой функцией называется функция [32], [61], получающаяся в результате замены непрерывной переменной на дискретную независимую переменную, определенную в дискретные моменты времени nТ, где n = 0, 1, 2, …
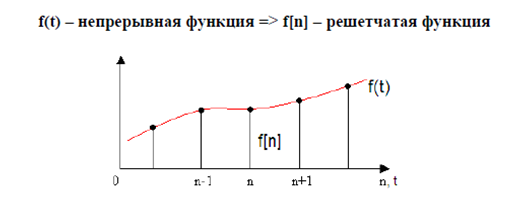
Непрерывной функции f(t) соответствует решетчатая функция f(nТ), где Т – период квантования, при этом непрерывная функция является огибающей решетчатой функции. При заданном значении периода квантования Т непрерывной функции f(t) соответствует однозначная решетчатая функция f(nТ). Однако обратного однозначного соответствия между решетчатой и непрерывной функцией не существует, так как через ординаты решетчатой функции можно провести множество огибающих.
Процедура преобразования сигнала непрерывного времени f(t) к дискретному виду, квантованному по времени, называется квантованием. В результате квантования получается импульсная последовательность f(kT) (решетчатая функция), которая при t = kT совпадает с исходным сигналом:
f(kT) = f(t)|t=nT,
и не определена между отсчетами n. Потери информации при квантовании зависят от величины интервала квантования Т (частоты квантования 2p/T).
Выбор интервала Т обычно осуществляется из соображений теоретической возможности точного восстановления исходного сигнала по данной дискретной выборке. Согласно теореме Котельникова-Шеннона, если спектр сигнала f(t) ограничен максимальной частотой wmax, то точное восстановление функции f(t) теоретически возможно при условии, что на одном периоде максимальной частоты в сигнале имеется минимум два дискретных отсчета, т.е. частота квантования w должна быть более чем в 2 раза больше наибольшей частоты wmax в сигнале: w ≥ 2wmax, T < p/wmax.
Связь между значениями решетчатой функции при разных значениях аргумента определяется с помощью конечных разностей, которые являются аналогами производных в дифференциальных уравнениях.
Разностью первого порядка (первой разностью) называется разность между последующим дискретным значением решетчатой функции и ее текущим значением: Df(n) = f(n+1) – f(n).

Разность первого порядка характеризует скорость изменения решетчатой функции и, следовательно, является аналогом первой производной непрерывной функции.
Разность второго порядка определяется как разность двух соседних разностей первого порядка:
D2f(n) = Df(n+1) - Df(n) = [f(n+2)-f(n+1)] – [f(n+1)-f(n)] = f(n+2) – 2f(n+1) + f(n).
Разности любого m-го порядка вычисляются аналогично:
Dmf(n) = Dm-1f(n+1) - Dm-1f(n).
Dmf(n) = 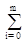 (-1)i f(n+m-i) m!/[n!(m-i)!].
(-1)i f(n+m-i) m!/[n!(m-i)!].
С использованием понятия разности в дискретной системе динамические процессы описываются так называемыми разностными уравнениями, являющимися аналогами однородного линейного дифференциального уравнения при описании непрерывных динамических систем.
При этом предполагается, что в моменты t = nT импульсные сигналы x(nT) полученной дискретной модели с определенной степенью точности повторяют значения сигналов x(t) исходной непрерывной системы.
C использованием разностных уравнений математическое описание линейных импульсных систем приводится к виду:
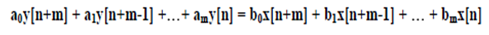 (6.2.1)
(6.2.1)
где уравнение (6.2.1) является линейным разностным уравнением с постоянными коэффициентами аm (m=0, 1, 2,...).
Решение (6.2.1) дает значение дискретной переменной y(n) для каждого периода квантования.
Таким образом, в дискретной системе (6.2.1) процессы в квантованные моменты времени t-nT точно совпадают с процессами в исходной непрерывной системе. Так как решения дискретной системы в промежуточные моменты времени не определены, то корректный переход к дискретной форме предусматривает выбор интервала квантования Т в соответствии с теоремой Котельникова-Шеннона.
Пример подобного описания дискретной системы [61] показан на рис.15.4.
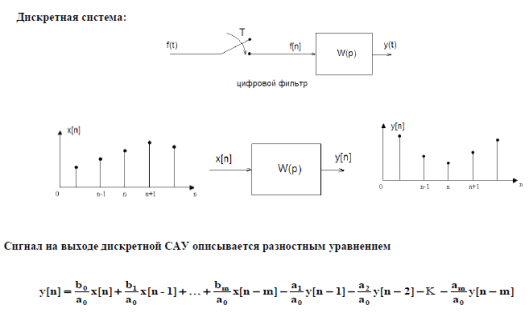
Рис.15.4
Порядок разностного уравнения определяется числом разностей выходной переменной.
Например. Определить порядок разностного уравнения
y[(n+2)T] + 0,2y[nT] = 5 x[nT],
где: T – период квантования времени, n = 0,1, … - дискретное время.
Ответ: порядок данного разностного уравнения равен 2.
Разностные уравнения являются рекуррентными соотношениями, позволяющими при n=0,1, 2, … последовательно пошагово (рекуррентно) вычислять значения выходной величины при заданных значениях входной.
В теории импульсных систем для решения разностных уравнений используется [32] дискретное преобразование Лапласа
F(p) =  f(nT) exp(-pnT). (6.2.4)
f(nT) exp(-pnT). (6.2.4)
Дискретное преобразование Лапласа используется также для исследования линейных дискретных систем.
Если ввести новую переменную z=exp(pT), то из (6.2.4) получим:
F(z) =  f(nT) z-n. (6.2.5)
f(nT) z-n. (6.2.5)
Эта последовательность представляет собой z-преобразование. Она лежит в основе метода решения разностных уравнений. При анализе дискретных систем z-преобразование позволяет перейти от разностных уравнений к алгебраическим и существенно упростить анализ динамики дискретных систем.
В выражении (6.2.5) функция f(nТ) называется оригиналом решетчатой функции, a F(z) – ее изображением.
Формула (6.2.5) может быть записана в символическом виде:
F(z) = Z{f(n)}.
Для последовательности, сдвинутой на целое число тактов m (теорема запаздывания), имеем
Z{f (n-m)} = z - m·F(z). (6.2.6)
Как и для анализа непрерывных систем, так и для дискретных большую роль играет передаточная функция. Она достаточно просто определяется по уравнению 6.2.1.
Переходя в разностном уравнении (6.2.6) к изображениям дискретное преобразование Лапласа позволяет получить связь дискретных изображений Лапласа выходной и входной переменных при нулевых начальных условиях в виде передаточной функции:
W(z) = Y(z) / U(z).
Здесь W(z) - дискретная передаточная функция, которая, как и в случае непрерывных функций, является отношением изображений выходной и входной функций при нулевых начальных условиях;
Y(z) - изображение выходной функции;
U(z) - изображение входной функции.
Как и для непрерывных функций, здесь имеется возможность по известной дискретной передаточной функции найти разностные уравнения описания СУ, так и наоборот.
Например. Написать передаточную функции системы, описываемой разностным уравнением y[(n+1)T] + 0,2y[nT] = 5 g[(n)T],
где: T – период квантования времени, n = 0,1, … - дискретное время,
Ответ. Wz = 5/(z + 0,2).
Также как и у непрерывных функций, корни полинома числителя являются нулями передаточной функции дискретной системы.
Корни полинома знаменателя являются полюсами передаточной функции дискретной системы.
Например.
Для замкнутой системы, описываемой разностным уравнением
y[(n+2)T] = 4y[(n+1)T] + 10g[nT],
где:: T – период квантования времени, n = 0,1, … - дискретное время,
g[*] – входная переменная, y[*] – выходная переменная;
найти корни характеристического уравнения.
Решение.
Характеристическое уравнение для данного разностного уравнения
z2 - 4 = 0, откуда корни: z1 = 0, z2 = 4.
Для замкнутой дискретной системы с единичной отрицательной обратной связью передаточная функция по задающему воздействию (рис.15.5)
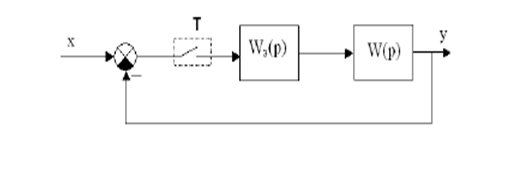
рис.15.5
Равна Ф(z) = W(z) / 1+ W(z)
Передаточная функция по ошибке (рис.15.6)
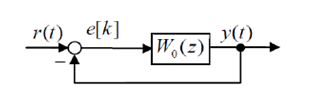
рис.15.6
Равна Ф(z) = 1 / 1+ W(z)
Определении 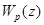 возможно непосредственно по
возможно непосредственно по 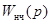 - передаточной функции непрерывной части [33]. В этом случае имеющийся в системе (рис. 15.10) импульсный элемент (ИЭ) заменяется последовательно соединёнными ключом K, работающим с периодом Т, и формирующим элементом (ФЭ) (рис. 15.11).
- передаточной функции непрерывной части [33]. В этом случае имеющийся в системе (рис. 15.10) импульсный элемент (ИЭ) заменяется последовательно соединёнными ключом K, работающим с периодом Т, и формирующим элементом (ФЭ) (рис. 15.11).

Рис. 15.10
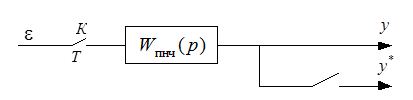
Рис. 15.11
При этом импульсная переходная функция 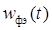 формирующего элемента совпадает с функцией, описывающей форму исходного (единичного) импульса. Поэтому передаточная функция
формирующего элемента совпадает с функцией, описывающей форму исходного (единичного) импульса. Поэтому передаточная функция 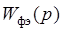 формирующего элемента определяется выражением
формирующего элемента определяется выражением
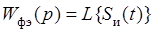 , (15.20)
, (15.20)
где 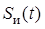 – функция, описывающая единичный импульс реального импульсного элемента;
– функция, описывающая единичный импульс реального импульсного элемента; 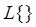 – обозначение непрерывного преобразования Лапласа.
– обозначение непрерывного преобразования Лапласа.
Например, если импульсный элемент системы формирует прямоугольные импульсы длительностью 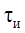 (цифроаналоговый преобразователь), то функция
(цифроаналоговый преобразователь), то функция 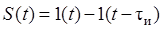 . Поэтому по формуле (15.20) для случая прямоугольных импульсов имеем
. Поэтому по формуле (15.20) для случая прямоугольных импульсов имеем
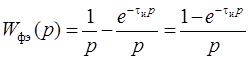 . (15.21)
. (15.21)
ЛЕКЦИЯ № 18
АНАЛИЗ ДСАУ
Анализ ДСАУ включает определение характера и степени устойчивости системы, параметров переходного процесса, точности установившегося режима.
Определение устойчивости дискретных систем имеет некоторые отличия от непрерывных систем. Для последних условием устойчивости является отрицательность корней характеристического уравнения системы
(рис.14.8. а) [60].

Рис.14.8.
Поскольку для дискретных систем используется другая переменная
z = e pT.
то её конформное преобразование отображает левую полуплоскость плоскости p в область, ограниченную окружностью единичного радиуса на плоскости z (рис.14.8. б). При этом мнимая ось плоскости p отображается в саму окружность.
Отсюда следует, что условие устойчивости линейных дискретных систем на плоскости z имеет вид
 . (15.48)
. (15.48)
Геометрически это условие означает, что на комплексной плоскости z все корни характеристического уравнения (15.47)
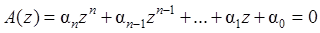 (15.47)
(15.47)
устойчивой линейной дискретной системы располагаются в круге
радиусом z =1.
Окружность единичного радиуса таким образом представляет собой границу устойчивости дискретной системы.
При этом возможны следующие варианты:
· если все корни характеристического уравнения находятся внутри указанной окружности, то система устойчива;
· если имеется корень zi=1, то система находится на границе устойчивости нейтрального типа (апериодическая граница устойчивости) (рис.14.8. в);
· если в характеристическом уравнении имеется пара сопряженных комплексных корней, расположенных на окружности единичного радиуса (рис.14.8. г), то имеет место колебательная граница устойчивости;
· если имеется корень zi=-1, то система имеет границу устойчивости третьего типа, характерную незатухающими периодическими колебаниями (рис.14.8. д).
Отсюда следует:
· вещественный положительный корень характеристического уравнения, по модулю меньший единицы | λ 1|<1, порождает в переходной составляющей решения разностного уравнения компоненту
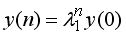 ,
,
которая будет экспоненциально затухать.
· вещественный отрицательный корень характеристического уравнения, по модулю меньший единицы | λ 1|<1, порождает в переходной составляющей решения разностного уравнения компоненту
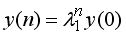 ,
,
которая будет колебательно затухать.
· вещественный положительный корень характеристического уравнения, по модулю больший единицы, | λ 1|>1, порождает в переходной составляющей решения разностного уравнения компоненту
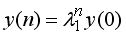 ,
,
которая будет экспоненциально возрастать.
Пример [33]. Исследовать устойчивость системы с характеристическим полиномом 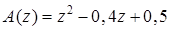 .
.
Решение. Корни заданного полинома, очевидно, равны 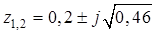 . Их модули
. Их модули 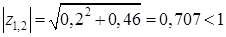 . Следовательно, заданная дискретная система является устойчивой.
. Следовательно, заданная дискретная система является устойчивой.
Исследование устойчивости линейных дискретных систем является более сложной задачей, чем исследование устойчивости непрерывных систем. Здесь неприменимы критерии Вышнеградского и Гурвица, также неприменимо условие положительности коэффициентов характеристического уравнения.
Например, в уравнении z - 0,5 = 0, один коэффициент отрицательный, но система тем не менее устойчива, т.к. соблюдается условие | z | < 1.
Для возможности использования в исследовании устойчивости линейных дискретных систем критериев устойчивости непрерывных систем используется так называемое билинейное или ω – преобразование. Смысл последнего в том, что применив новую переменную ω
Z = 1 + ω / 1 - ω
круг единичного радиуса с плоскости Z отображается на левую плоскость вновь введенной переменной ω.
Это преобразование позволяет применить к полиному относительно переменной ω критерий Гурвица. Если характеристический полином 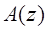 преобразован к А (ω), и последний удовлетворяет критерию Гурвица, то дискретная система с данным полиномом
преобразован к А (ω), и последний удовлетворяет критерию Гурвица, то дискретная система с данным полиномом 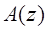 асимптотически устойчива.
асимптотически устойчива.
Степень устойчивости дискретных систем на плоскости z равна разности [33]:
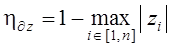 , (15.51)
, (15.51)
где 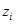 – корни характеристического уравнения A (z) (15.47) замкнутой дискретной системы.
– корни характеристического уравнения A (z) (15.47) замкнутой дискретной системы.
На комплексной плоскости р соответствующая степень устойчивости дискретной системы определяется по формуле
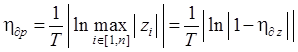 . (15.52)
. (15.52)
Здесь T – период квантования по времени в исследуемой системе.
Если система является неустойчивой, то запасы устойчивости не определяются.
Пример. Найти степени устойчивости системы, которая описывается уравнением
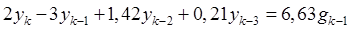 , (15.53)
, (15.53)
а период квантования T = 0,1 с.
Решение. Корни характеристического уравнения системы (15.53) (найдены с помощью функции roots из пакета MATLAB) равны 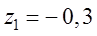 ;
; 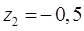 ;
; 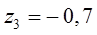 . Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы
. Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы 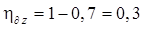 , а на плоскости p –
, а на плоскости p – 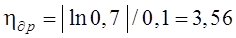 .
.
Переходные процессы дискретных систем [33].
Показатели качества дискретных (естественно, устойчивых) систем и методы их исследования практически полностью аналогичны случаю непрерывных систем. Это касается управляемости, наблюдаемости, астатизма, показателей качества в переходном и установившемся режимах.
Дискретные системы в переходном периоде также характеризуются временем переходного процесса, перерегулированием и т.д., где эти характеристики имеют тот же смысл.
Рассмотрим отличительные особенности и порядок построения переходных процессов дискретных систем.
Условия конечной длительности. Одной из важных особенностей дискретных систем является возможность обеспечения переходных процессов конечной длительности. Такой переходной процесс длится ровно n периодов квантования, где n – порядок системы. Условия существования переходного процесса конечной длительности определяются следующей теоремой.
Теорема. Если знаменатель передаточной функции 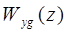 дискретной системы по некоторому воздействию
дискретной системы по некоторому воздействию 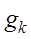 равен
равен 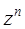 , т.е.
, т.е.
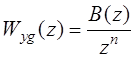 . (15.54)
. (15.54)
то переходный процесс данной системы по этому воздействию длится ровно n периодов T квантования по времени.
Пример 15.13. Найти длительность переходного процесса дискретной системы с передаточной функцией 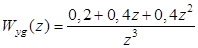 при
при 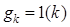 и нулевых начальных условиях, если
и нулевых начальных условиях, если 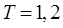 с.
с.
Решение. Воспользуемся рекуррентным методом решения разностных уравнений. В данном случае это уравнение имеет вид 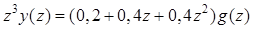 . Разделим обе его части на
. Разделим обе его части на 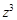 и перейдём к оригиналам. В результате получим
и перейдём к оригиналам. В результате получим 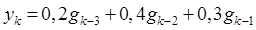 .
.
Полагая последовательно в этом выражении 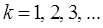 , будем иметь
, будем иметь 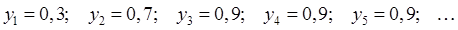 Как видно, в полном соответствии с условием (15.54), через три такта выходная переменная принимает установившееся значение 0,9; т.е. переходный процесс длится ровно три периода квантования по времени, и его длительность
Как видно, в полном соответствии с условием (15.54), через три такта выходная переменная принимает установившееся значение 0,9; т.е. переходный процесс длится ровно три периода квантования по времени, и его длительность 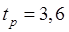 с. При этом предыдущие значения выходной переменной не влияют на её последующие значения ни при каком k.
с. При этом предыдущие значения выходной переменной не влияют на её последующие значения ни при каком k.
Условие (15.54) приведенной теоремы, при котором обеспечивается конечная длительность переходных процессов дискретных систем, часто применяется при создании систем управления с заданной длительностью переходных процессов. Иногда такие дискретные системы называются оптимальными по быстродействию.
Астатизм дискретных систем[33].
Свойство астатизма дискретных систем, как отмечалось выше, аналогично свойству астатизма непрерывных систем. Однако имеется ряд особенностей, обусловленных квантованием переменных по времени.
Определение. Астатической называют дискретную систему, статическая ошибка которой равна нулю. В противном случае систему называют статической.
Приведенному определению удовлетворяют два типа дискретных систем. У систем первого типа ошибка при постоянном входном воздействии равна нулю как в моменты времени, кратные периоду квантования T, так и во все остальные. В то же время у астатических систем второго типа ошибка при постоянном входном воздействии равна нулю только в моменты времени, кратные периоду квантования T, а во все остальные моменты ошибка не является нулевой.
Порядок астатизма в случае дискретных систем, также как и в непрерывном случае, можно оценивать либо по заданной структурной схеме, либо по передаточной функции по ошибке, либо по передаточной функции системы в разомкнутом состоянии (при главной единичной обратной связи), либо по передаточной функции системы в замкнутом состоянии.
Признак астатизма дискретных систем по 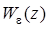 . Изображение сигнала ошибки, вызванной, например, воздействием gk, можно записать при нулевых начальных условиях следующим образом:
. Изображение сигнала ошибки, вызванной, например, воздействием gk, можно записать при нулевых начальных условиях следующим образом:
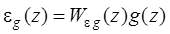 , (15.55)
, (15.55)
где 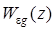 – передаточная функция системы по ошибке, вызванной воздействием gk.
– передаточная функция системы по ошибке, вызванной воздействием gk.
Признаки астатизма дискретных систем по 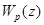 . Вид этих признаков зависит от типа системы, от вида обратной связи, и от того является ли рассматриваемое воздействие задающим или возмущающим. Рассмотрим здесь случай, когда система является системой стабилизации, программного управления или следящей, а обратная связь является единичной и отрицательной, т.е. тот случай, когда передаточная функция по ошибке, обусловленной задающим воздействием gk, определяется выражением
. Вид этих признаков зависит от типа системы, от вида обратной связи, и от того является ли рассматриваемое воздействие задающим или возмущающим. Рассмотрим здесь случай, когда система является системой стабилизации, программного управления или следящей, а обратная связь является единичной и отрицательной, т.е. тот случай, когда передаточная функция по ошибке, обусловленной задающим воздействием gk, определяется выражением
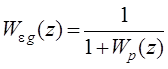 . (15.56)
. (15.56)
СИНТЕЗ ЦСАУ
Задача синтеза цифровых устройств управления заключается в подборе функционально необходимых элементов и установлении связей между ними для выполнения системой поставленной задачи с определенными критериями качества. При построении САУ для придания им новых характеристик часто используются корректирующие устройства.
В любом случае может применяться последовательное и параллельное включения элементов, а также включение с обратной связью (ОС) [61].
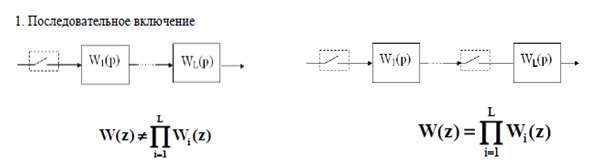
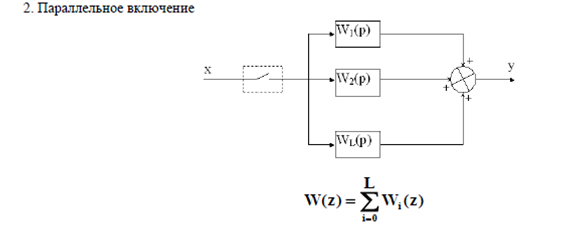
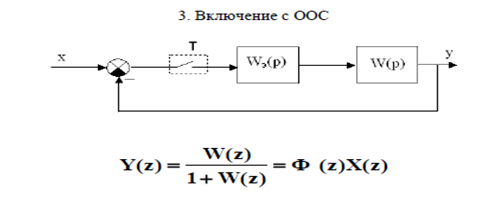
Здесь также используются для замкнутой дискретной системы с единичной отрицательной обратной связью передаточная функция по задающему воздействию (рис.15.5) и передаточная функция по ошибке (рис.15.6)
В тех случаях, когда замкнутая дискретная система, составленная из функционально необходимых элементов, является неустойчивой, или её показатели качества не удовлетворяют требуемым, возникает задача её коррекции или задача синтеза устройства управления. В настоящее время наиболее рациональным путем построения устройств управления является использование управляющих вычислительных машин (рис. 16.1)
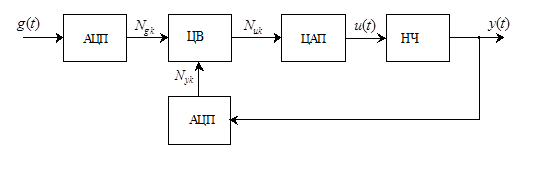
Рис. 16.1
или специализированных цифровых вычислителей (ЦВ) – микропроцессоров или микроЭВМ.
При выбранном законе управления, например в виде (16.1) или (16.2),
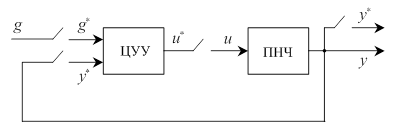
Рис. 16.2
задача синтеза сводится к определению численных значений его параметров настройки. Однако в общем случае для обеспечения повышенных требований к качеству системы (например, второй или третий порядок астатизма, небольшое время регулирования и перерегулирование) простейшие законы управления оказываются недостаточными. В этом случае применяют более сложные алгоритмы вычисления значений управления uk. Процедура синтеза соответствующих законов управления включает определение и структуры, и параметров ЦУУ.
Используются следующие методы синтеза указанных законов дискретных управлений.
Дискретное модальное управление, по аналогии с непрерывным, ищется в виде
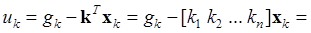
 . (16.5)
. (16.5)
Коэффициенты ki здесь, как и в непрерывном случае, выбираются так, чтобы корни характеристического уравнения замкнутой системы (16.4), (16.5) имели заданные значения.
Синтез дискретных систем по заданным показателям качества, где предполагается, что в соответствии с техническим заданием необходимо синтезировать систему управления с астатизмом первого порядка по задающему воздействию и с определенными первичными показателями качества такими, как время регулирования и перерегулирование. Фактически здесь требуется найти разностное уравнение, описывающее алгоритм работы ЦУУ, при котором указанные первичные показатели качества синтезированной замкнутой системы будут не хуже заданных.
Синтез корректирующих устройств дискретных систем как для непрерывных систем удобен и нагляден также с использованием логарифмических частотных характеристик.
Естественно, круг методов синтеза САУ значительно шире, чем указан выше, но это уже не входит в тематику данного учебного пособия.
JBIG — это стандарт сжатия изображений без потерь, предложенный Группой Экспертов в Сжатии Бинарных Изображений (Joint Bi-level Image Experts Group), и стандартизованный Международной Организацией по стандартизации ISO/IEC стандарт номер 11544 и как ITU-T рекомендации T.82 Позднее был принят более новый стандарт сжатия бинарных (только два любых цвета — чёрный и белый, серый и зелёный, красный и синий и т. д.) изображений JBIG2, JBIG также известен как JBIG1. JBIG был разработан в первую очередь для сжатияфаксимильных изображений, но может также достаточно эффективно быть использован и для других классов изображений. В большинстве случаев JBIG демонстрирует приблизительно на 20-50 % лучшую степень сжатия по сравнению с более простым и раньше появившимся стандартом Fax Group 4, в некоторых ситуация преимущество достигает нескольких раз. Алгоритм разработан для сжатия изображения по строкам в порядке их поступления. Также JBIG поддерживается прогрессивная передача (постепенное «проявление» изображения на приёмнике по мере получения файла) с небольшим (порядка 5 %) понижением степени сжатия
[1] У некоторых авторов используется термин – переходная составляющая







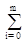 (-1)i f(n+m-i) m!/[n!(m-i)!].
(-1)i f(n+m-i) m!/[n!(m-i)!].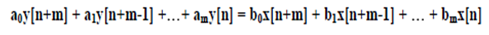 (6.2.1)
(6.2.1)

 f(nT) exp(-pnT). (6.2.4)
f(nT) exp(-pnT). (6.2.4)

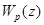 возможно непосредственно по
возможно непосредственно по 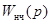 - передаточной функции непрерывной части [33]. В этом случае имеющийся в системе (рис. 15.10) импульсный элемент (ИЭ) заменяется последовательно соединёнными ключом K, работающим с периодом Т, и формирующим элементом (ФЭ) (рис. 15.11).
- передаточной функции непрерывной части [33]. В этом случае имеющийся в системе (рис. 15.10) импульсный элемент (ИЭ) заменяется последовательно соединёнными ключом K, работающим с периодом Т, и формирующим элементом (ФЭ) (рис. 15.11).
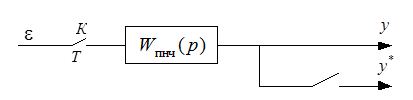
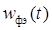 формирующего элемента совпадает с функцией, описывающей форму исходного (единичного) импульса. Поэтому передаточная функция
формирующего элемента совпадает с функцией, описывающей форму исходного (единичного) импульса. Поэтому передаточная функция 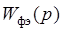 формирующего элемента определяется выражением
формирующего элемента определяется выражением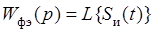 , (15.20)
, (15.20)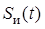 – функция, описывающая единичный импульс реального импульсного элемента;
– функция, описывающая единичный импульс реального импульсного элемента; 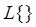 – обозначение непрерывного преобразования Лапласа.
– обозначение непрерывного преобразования Лапласа.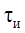 (цифроаналоговый преобразователь), то функция
(цифроаналоговый преобразователь), то функция 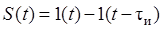 . Поэтому по формуле (15.20) для случая прямоугольных импульсов имеем
. Поэтому по формуле (15.20) для случая прямоугольных импульсов имеем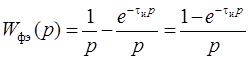 . (15.21)
. (15.21)
 . (15.48)
. (15.48)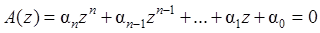 (15.47)
(15.47)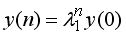 ,
,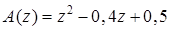 .
.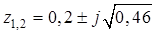 . Их модули
. Их модули 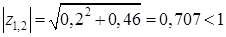 . Следовательно, заданная дискретная система является устойчивой.
. Следовательно, заданная дискретная система является устойчивой.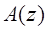 преобразован к А (ω), и последний удовлетворяет критерию Гурвица, то дискретная система с данным полиномом
преобразован к А (ω), и последний удовлетворяет критерию Гурвица, то дискретная система с данным полиномом 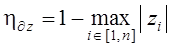 , (15.51)
, (15.51)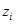 – корни характеристического уравнения A (z) (15.47) замкнутой дискретной системы.
– корни характеристического уравнения A (z) (15.47) замкнутой дискретной системы.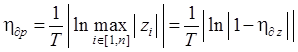 . (15.52)
. (15.52)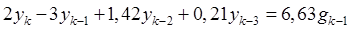 , (15.53)
, (15.53)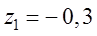 ;
; 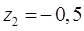 ;
; 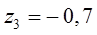 . Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы
. Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы 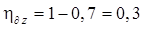 , а на плоскости p –
, а на плоскости p – 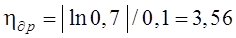 .
.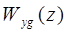 дискретной системы по некоторому воздействию
дискретной системы по некоторому воздействию 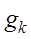 равен
равен 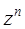 , т.е.
, т.е.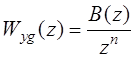 . (15.54)
. (15.54)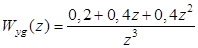 при
при 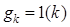 и нулевых начальных условиях, если
и нулевых начальных условиях, если 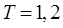 с.
с.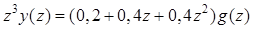 . Разделим обе его части на
. Разделим обе его части на 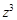 и перейдём к оригиналам. В результате получим
и перейдём к оригиналам. В результате получим 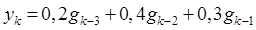 .
.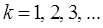 , будем иметь
, будем иметь 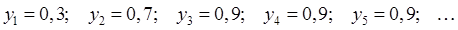 Как видно, в полном соответствии с условием (15.54), через три такта выходная переменная принимает установившееся значение 0,9; т.е. переходный процесс длится ровно три периода квантования по времени, и его длительность
Как видно, в полном соответствии с условием (15.54), через три такта выходная переменная принимает установившееся значение 0,9; т.е. переходный процесс длится ровно три периода квантования по времени, и его длительность 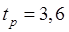 с. При этом предыдущие значения выходной переменной не влияют на её последующие значения ни при каком k.
с. При этом предыдущие значения выходной переменной не влияют на её последующие значения ни при каком k.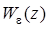 . Изображение сигнала ошибки, вызванной, например, воздействием gk, можно записать при нулевых начальных условиях следующим образом:
. Изображение сигнала ошибки, вызванной, например, воздействием gk, можно записать при нулевых начальных условиях следующим образом: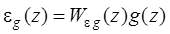 , (15.55)
, (15.55)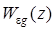 – передаточная функция системы по ошибке, вызванной воздействием gk.
– передаточная функция системы по ошибке, вызванной воздействием gk.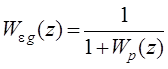 . (15.56)
. (15.56)




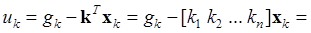
 . (16.5)
. (16.5)


