

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Принято считать [33], что установившийся режим работы системы начинается с момента окончания переходного процесса tp и продолжается до бесконечности, как показано на рис. 5.6.

Рис 5.6
Качество работы любой системы управления в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным значениями управляемой величины.
Таким образом точностные характеристики систем относятся к установившемуся режиму рис.5.6. и оцениваются с помощью статических и динамических ошибок. Эти ошибки можно назвать основным показателем качества системы в установившихся режимах. Кроме того, для отдельных систем используются и прочие показатели, например, порядок астатизма системы – ν и др.
Для статических систем ошибку (точность САУ) можно [39] графически показать, как параметр – e (см.рис. 5.7):
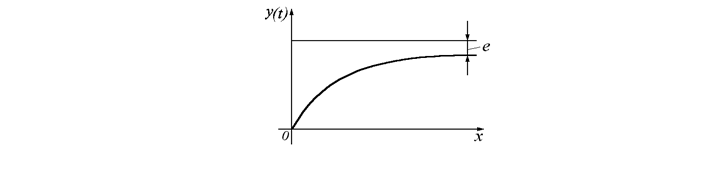
Рис. 5.7
При этом величина ошибки равна: 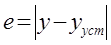
Основным показателем качества САУ в установившемся режиме является её установившаяся ошибка, которая в общем случае определяется выражением
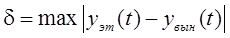 , (5.5)
, (5.5)
где
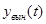 – вынужденная составляющая управляемой переменной системы (т.е. частное решение дифференциального уравнения САУ, обусловленное некоторым воздействием);
– вынужденная составляющая управляемой переменной системы (т.е. частное решение дифференциального уравнения САУ, обусловленное некоторым воздействием);
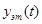 – желаемый закон изменения управляемой переменной системы под влиянием данного воздействия или задающее воздействие - g (t);
– желаемый закон изменения управляемой переменной системы под влиянием данного воздействия или задающее воздействие - g (t);
Таким образом, установившаяся ошибка характеризует точность системы в статическом режиме и равна отклонению действительного значения регулируемой величины от заданного.
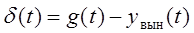 ,
,
Отношение ν = δcm.g / g 0 иногда называется статизмом системы по задающему воздействию. Соответственно обратная величина 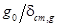 называется добротностью системы управления.
называется добротностью системы управления.
В зависимости от значения статической ошибки системы управления делятся на статические системы (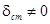 ) и астатические системы (
) и астатические системы (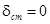 ).
).
Если функция g (t) дифференцируема во всем интервале 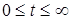 , то ошибка САУ может быть представлена в виде ряда
, то ошибка САУ может быть представлена в виде ряда
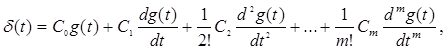
где C 0– коэффициент статической или позиционной ошибки;
C 1– коэффициент скоростной ошибки;
C 2– коэффициент ошибки от ускорения и т.д.
Коэффициенты ошибок C 0, C 1, C 2, …, Cm определяют по формулам разложения ПФ по ошибке Fe(s) в ряд Тейлора
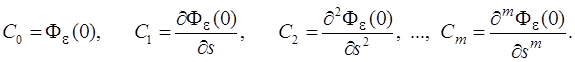
Если воздействие g (t) является единичным ступенчатым, то все его производные будут равны нулю
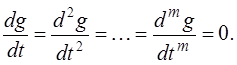
В этом случае установившаяся ошибка согласно (2.137):
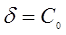 , где
, где 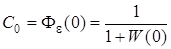
Если g (t) = t, то 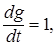 а
а 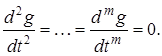
Установившаяся ошибка при этом
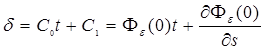 .
.
Коэффициент статической ошибки статической САУ 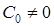 , так как
, так как 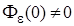 и ПФ разомкнутой САУ
и ПФ разомкнутой САУ  . Астатические САУ с астатизмом первого порядка имеют
. Астатические САУ с астатизмом первого порядка имеют 
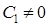 ,
, 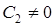 .
.
Системы с астатизмом второго порядка имеют 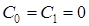 , а коэффициент ошибки от ускорения
, а коэффициент ошибки от ускорения 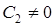 .
.
Увеличение количества И-звеньев в САУ приводит к повышению порядка астатизма, т.е. к нулевым значениям нескольких коэффициентов ошибок, но при этом снижается запас устойчивости системы.
Если к САУ помимо управляющего воздействия g (t) приложено возмущающее воздействие f (t), то астатизм системы относительно g (t) и f (t) зависит от места включения И-звена.
ПФ разомкнутой статической САУ W (0) = K при s = 0, поэтому следует, что статическая ошибка  .
.
Таким образом, для уменьшения ошибки необходимо добиваться достаточно большого коэффициента усиления K разомкнутой САУ.
С увеличением коэффициента усиления К разомкнутой системы установившиеся ошибки уменьшаются. Однако с возрастанием К ухудшается устойчивость автоматических систем, т.е. требование к точности противоречит требованию к устойчивости. При заданном относительно большом значении К улучшение устойчивости достигается включением в систему корректирующих устройств.
В этом случае требуемый для обеспечения заданной ошибки регулирования δ коэффициент усиления САУ к тр определяется из выражения
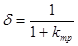 ;
;
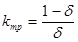 .
.
Если коэффициент усиления разомкнутой исходной системы 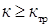 , то это значит, что исходная система отвечает требованиям задания по точности.
, то это значит, что исходная система отвечает требованиям задания по точности.
В случае систем стабилизации, программного управления или следящих систем [33] эталонная переменная 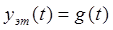 , где g (t) – задающее воздействие, εg – отклонение системы, обусловленное действием только задающего воздействия g (t).
, где g (t) – задающее воздействие, εg – отклонение системы, обусловленное действием только задающего воздействия g (t).
Тогда ошибка
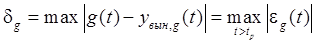 . 5.6)
. 5.6)
Другими словами, в тех случаях, когда 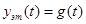 , сигналом ошибки является отклонение или рассогласование системы управления с отрицательной единичной обратной связью.
, сигналом ошибки является отклонение или рассогласование системы управления с отрицательной единичной обратной связью.
Задачи стабилизации и слежения иначе могут быть сформулированы как задачи поддержания нулевого значения рассогласования, т. е. e(t) → 0.
Так как 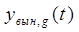 существенно зависит от вида входного воздействия
существенно зависит от вида входного воздействия 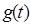 , то ошибки САУ классифицируются в зависимости от вида воздействий.
, то ошибки САУ классифицируются в зависимости от вида воздействий.
Определение ошибки по возмущающему воздействию 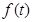 отличается тем, что в формуле (5.5)
отличается тем, что в формуле (5.5) 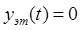 , т.е.
, т.е.
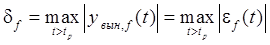 , (5.7)
, (5.7)
где  – вынужденная составляющая выходной величины, а
– вынужденная составляющая выходной величины, а 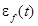 – отклонение системы, обусловленное действием только возмущения
– отклонение системы, обусловленное действием только возмущения 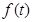 .
.
Ошибки, определяемые выражениями (5.5) – (5.7), называются структурными, так как в первую очередь определяются именно структурой системы управления. Если воздействие имеет определенный (регулярный) тип, то, как будет показано ниже, выбором структуры системы эту ошибку практически всегда можно сделать равной нулю. Поэтому формально можно считать, что если структурная ошибка системы, вызванная некоторым воздействием определенной формы, не равна нулю, то структура системы является неудачной по отношению к данному воздействию.
Различают следующие структурные ошибки.
Статическая ошибка. В этом случае 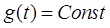 (часто полагают
(часто полагают 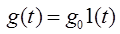 . Здесь
. Здесь 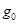 – интенсивность задающего воздействия, постоянного по величине).
– интенсивность задающего воздействия, постоянного по величине).
При 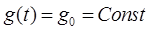 можно записать:
можно записать: 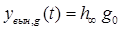 . Тогда, если
. Тогда, если 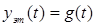 , то согласно (5.6) статическая ошибка по задающему воздействию
, то согласно (5.6) статическая ошибка по задающему воздействию 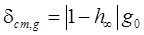 .
.
Динамическая ошибка. Эта ошибка определяется по формулам (5.5), (5.6) или (5.7) при условии, что воздействие является полиномиальной функцией некоторой степени, т.е., например, 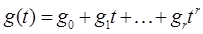 , где
, где 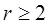 , или какой-либо другой функцией времени (но не периодической).
, или какой-либо другой функцией времени (но не периодической).
Ошибки по модулю и по фазе. Для оценки качества САУ в условиях колебательных воздействий применяются ошибка по модулю и ошибка по фазе.
Входной сигнал при этом считается гармоническим, например, 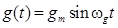 . Его частота
. Его частота 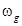 выбирается близкой к частотам колебаний реальных воздействий данной системы. В этом случае
выбирается близкой к частотам колебаний реальных воздействий данной системы. В этом случае  , причём амплитуда
, причём амплитуда 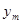 и фаза
и фаза 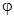 зависят от частоты
зависят от частоты 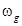 , т.е.
, т.е. 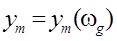 ,
, 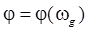 . Сигнал ошибки
. Сигнал ошибки 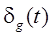 в этом случае также является гармоническим, т.е.
в этом случае также является гармоническим, т.е.
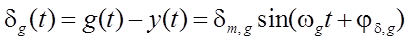 ,
, 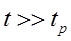 .
.
Поэтому здесь 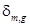 – ошибка по модулю, а
– ошибка по модулю, а 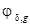 – ошибка по фазе.
– ошибка по фазе.
Для вычисления этих ошибок удобнее всего воспользоваться передаточными функциями по ошибке. Например,
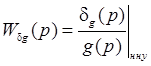 .
.
Полагая здесь 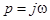 , будем иметь
, будем иметь
 .
.
Отсюда, в соответствии с определением ошибок по модулю и по фазе, вытекают формулы:
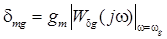 ,
, 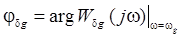 , (5.8)
, (5.8)
где 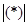 – обозначение модуля функции (*).
– обозначение модуля функции (*).
Совершенно аналогично с использованием соответствующих передаточных функций определяются ошибки САУ, вызванные другими колебательными воздействиями.
Иногда на систему действуют и колебательные, и не колебательные воздействия. Тогда для определения общей ошибки системы используют либо формулу
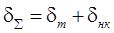 , либо
, либо 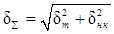 ,
,
где 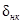 – ошибка, вызванная не колебательным воздействием.
– ошибка, вызванная не колебательным воздействием.
Аналогично суммарная ошибка, вызванная одновременным действием задающего воздействия g и возмущения f, определяется по формуле
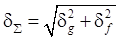 .
.
Среднеквадратическая ошибка. Когда система функционирует в условиях случайных воздействий, её точность оценивается по среднеквадратической ошибке 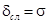 .
.
В этом случае сигнал ошибки 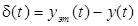 является случайным процессом и характеризуется средним значением
является случайным процессом и характеризуется средним значением 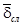 , корреляционной функцией
, корреляционной функцией 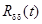 и дисперсией
и дисперсией 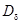 .
.
Среднеквадратическая ошибка (СКО) определяется выражением
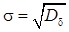 . (5.9)
. (5.9)
Среднее значение 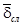 относят к статической ошибке системы.
относят к статической ошибке системы.
Поэтому полная структурная ошибка системы при наличии случайных воздействий определяется по формуле
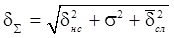 , (5.10)
, (5.10)
где 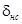 – структурная неслучайная ошибка, вызванная регулярными составляющими задающего и возмущающих воздействий.
– структурная неслучайная ошибка, вызванная регулярными составляющими задающего и возмущающих воздействий.
Уравнения, описывающие динамику системы (Рис.4.1), при переходе от функций времени к их изображениям по Лапласу, могут быть представлены в следующей общей форме [43]:
X(s) = Фxg (s)G(s) + Фxf (s)F(s), (4.4)
Y(s) = Фg (s)G(s) − Фf (s)F(s), (4.5)
где
G(s), F(s), X(s), Y(s) - изображения по Лапласу задающего, возмущающего воздействий, рассогласования (ошибки) и управляемой величины.
Фхg (s) - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
Фхf (s) - передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.
Фg(s) - передаточная функция замкнутой системы по задающему воздействию, главный оператор системы Ф(s).
Фf(s) - передаточная функция замкнутой системы по возмущающему воздействию.
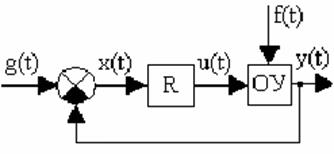
Рис. 4.1. Функциональная схема системы управления
Одно из основных требований, которым должна удовлетворять система управления, заключается в обеспечении необходимой точности воспроизведения задающего воздействия в установившемся режиме.
Для оценки точности системы определяется установившаяся ошибка, которая может быть получена из выражения (4.4) с помощью теоремы операционного исчисления о конечном значении функции:
x(∞) = lim x(t) = lim sX(s) = lim sФxg (s)· G(s)+ lim sФxf (s) ·F(s) =
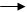
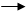
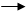
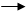
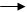 t ∞ s 0 s 0 s 0
t ∞ s 0 s 0 s 0
= xg (∞) + xf (∞) (6.4)
где xg (∞) - установившаяся ошибка от задающего воздействия;
xf (∞) - установившаяся ошибка от возмущающего воздействия.
Если задающее воздействие g(t) имеет произвольный характер, то изображение ошибки по задающему воздействию имеет вид:
Xg(s)= Фxg(s)G(s),
где Фxg(s) - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
Ошибку в замкнутой САУ [55] как показано выше можно представить:
ε(s) = W ε(s)· g(t)
где W ε(s) – передаточная функция замкнутой САУ по ошибке.
Передаточная функция ошибки воспроизведения задания определяется по ПФ разомкнутой системы как
W ε(s) = 1/[1 + W (s)],
по передаточной функции замкнутой системы как
W ε(s) = 1 – W зам(s).
Передаточная функция замкнутой системы:
W зам(s) = W(s)/[1 + W(s)],
Тогда передаточной функции замкнутой системы по ошибке, выраженная через ПФ разомкнутой системы, равна
W ε(s) = 1 –W(s)/[1 + W(s)] = 1/[1 + W(s)],
Максимально значение ошибки ε max можно оценить, исходя из выражения
ε(s) = g(t) /│1 + W(s)│,
Имея ввиду, что Фxg(s) =Wε(s) можно записать:
Xg(s)= G(s) / │1 + W(s)│.
Тогда, в системе с единичной обратной связью и передаточной функцией разомкнутого контура W(s) амплитуда ошибки Х при гармоническом входном воздействии амплитудой G и частотой 𝟂k может быть вычислена по формуле:
Xg(s)= G(s) / │1 + W(j 𝟂k)│.
ЛЕКЦИЯ № 13
|
|
|

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!