Детерминированные и стохастические системы

Системы, для которых состояние системы однозначно определяется начальными значениями и может быть предсказано для любого момента времени называются детерминированными.

Стохастические системы - системы изменения, в которых носят случайный характер. Например, влияние автомобильных пробок на регулярность полётов в аэропорту или неравномерный пассажиропоток к стойке регистрации пассажиров в аэропорту. При случайных воздействиях, данных о состоянии системы недостаточно для предсказания в последующий момент времени.

Расчет систем при случайных воздействиях производится с помощью специальных статистических методов. Вводятся оценки случайных параметров, выполненные на основании множества испытаний.

Статистические свойства случайной величины определяют по ее функции распределения или плотности вероятности.

Классификации всегда относительны. Так, в детерминированной системе можно найти элементы стохастичности, и, напротив, детерминированную систему можно считать частным случаем стохастической (при вероятности равной единице). Аналогично, если принять во внимание диалектику субъективного и объективного в системе, то станет понятной относительность разделения системы на абстрактные и объективно существующие: это могут быть стадии развития одной и той же системы.

Основные понятия в исследовании операций

Исследование операций — дисциплина, занимающаяся разработкой и применением методов нахождения оптимальных решений на основе математического моделирования, статистического моделирования и различных эвристических подходов в различных областях человеческой деятельности. Иногда используется название математические методы исследования операций.

Исследование операций — применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности. Исследование операций начинается тогда, когда для обоснования решений применяется тот или другой математический аппарат.

Операция — всякое мероприятие (система действий), объединённое единым замыслом и направленное к достижению какой-то цели. Операция всегда является управляемым мероприятием, т.е. зависит от ЛПР, каким способом выбрать параметры ресурсов необходимых при организации операции.

Решение — всякий определённый набор зависящих от ЛПР параметров. Оптимальное решение, решение которое по тем или другим критериям предпочтительнее других.

Цель исследования операций — предварительное количественное обоснование оптимальных решений с опорой на показатель эффективности. Результатом исследования операций, является выработка эффективного принятия решения проблем для ЛПР в детерминированных или стохастических системах.

Элементы решения — параметры, совокупность которых образует решение: числа, векторы, функции, физические признаки и т.д. Если элементами решения можно распоряжаться в определённых пределах, то заданные условия (ограничения) фиксированы сразу и нарушены быть не могут (грузоподъёмность, размеры, вес). К таким условиям относятся средства (материальные, технические, людские), которыми человек вправе распоряжаться, и иные ограничения, налагаемые на решение. Их совокупность формирует множество возможных решений.

Пример: Имеются m пунктов отправления груза А ₁, А ₂,..., А_m и объемы отправления по каждому пункту a ₁, a ₂,..., a_m. Известна потребность в грузах b ₁, b ₂,..., b_n по каждому из n пунктов назначения B ₁, B ₂,..., B_n. Задана также матрица стоимостей сij, (i =1,2,..., m, j =1,2,..., n) доставки груза из пункта i в пункт j. Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза xij должно быть отправлено из каждого пункта отправления (от поставщика) в каждый пункт назначения (до потребителя) с минимальными суммарными транспортными издержками.

Решение — совокупность чисел x ₁₁, x ₁₂, …, x_{m 1}, x_{m 2}, …, x_mn

1.5. Моделирование методами сетевого планирования

Сетевое планирование - метод научного планирования и управления производственными процессами, выполняющими большие объемы работ.

Методы сетевого планирования находят широкое применение во многих отраслях народного хозяйства, в том числе и на автомобильном транспорте.

На автомобильном транспорте методами сетевого планирования описываются процессы технического обслуживания и ремонта автомобилей, перевозочные и строительные процессы и т.д.

Сетевое планирование имеет ряд преимуществ:

- обеспечивает наглядность технологической последовательности работ;

- позволяет составить оперативные и текущие планы, а также прогнозировать сложные процессы;

- позволяет выявить скрытые ресурсы времени и материальных средств при выполнении производственных процессов и значительно повысить их эффективность.

Чтобы приступить к сетевому планированию (моделированию) того или иного производственного процесса, необходимо иметь перечень, последовательность и продолжительность (трудоемкость) выполнения операций (работ), соответствующих рассматриваемому производственному процессу.

Сетевое планирование сопровождается построением рабочих таблиц и сетевых графиков, к рассмотрению элементов которых мы и перейдем.

Элементы сетевых графиков

При построении сетевых графиков используют два логических понятия (элемента) - работа и событие.

В сетевом планировании термин «работа» предусматривает процесс, предшествующий совершению какого-либо события. Термин «событие» выражает собой определенный результат выполнения работы (или работ).

На сетевом графике события изображают кружком, а работы - ориентированными стрелками.

Фрагмент сетевого графика приведен на рис. 2.

 

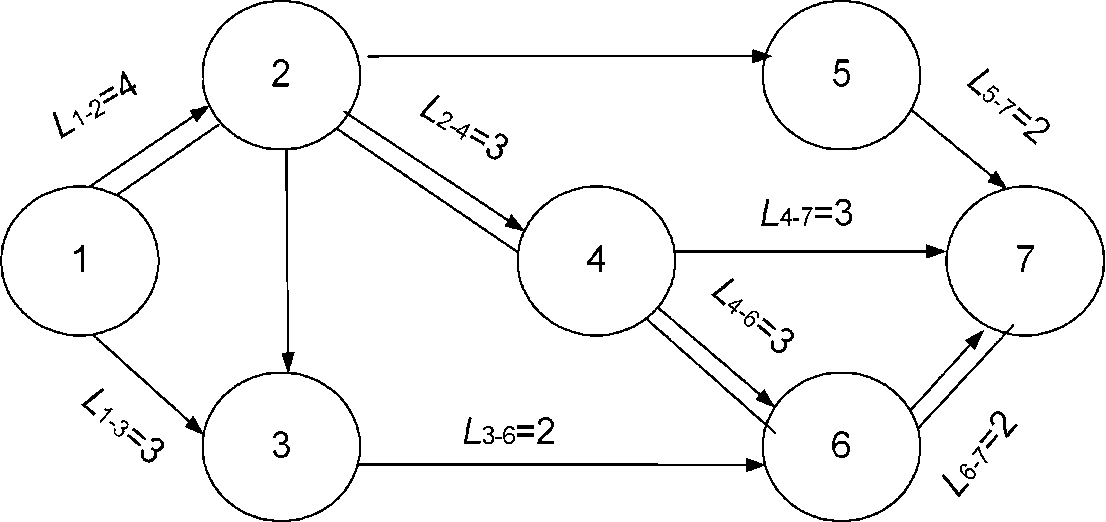
Рис. 2. Фрагмент сетевого графика

Каждому событию присваивается определенный номер (обычно цифрой), т.е. 1, 2, 3 и т.д.

Каждая работа, изображенная на сетевом графике стрелкой, объединяет только два события, поэтому принято работу на сетевом графике обозначать номерами предшествующего (i-го) и последующего (j-го) событий, т.е. 1 - 2,
2 - 5, 5 - 7 и т.д.

Продолжительность работы проставляется над стрелками, т. е. L_1-2 = 4,
L_2-5 = 5 и т.д.

Сетевой график представляет собой последовательность работ и событий, отражающих их технологическую взаимосвязь.

На сетевом графике выделяют два события: начальное (1) (исходное) и конечное (7) (завершающее). Все остальные события называются промежуточными.

Исходное событие отражает начало выполнения всего комплекса работ и не имеет предшествующего события.

Завершающееся событие отражает конечную цель всего комплекса работ и не имеет последующего события.

Термин «работа» включает три понятия:

1. «Фактическая работа», т.е. трудовой процесс, приводящий к достижению определенных результатов и требующих затрат времени и ресурсов.

2. «Ожидание» - технологический перерыв в работе, не требующий затрат труда, но требующий затрат времени (высыхание краски, отвердевание цемента и т.д.).

3. «Зависимость» (фиктивная работа) - логическая связь между событиями, не требующая затрат времени и ресурсов, но показывающая, что возможность начала одной работы зависит от результатов другой.

На сетевых графиках фактическую работу и ожидание изображают сплошными стрелками, а зависимости - пунктирными.

Сетевой график строят в масштабе или без масштаба. В последнем случае обязательно над стрелками проставляют продолжительность работы в единицах времени.

Любая последовательность работ от одного события к другому (любому) называется путем и обозначается L (2 - 5 - 7), т. е. каждый путь обозначают буквой L и номерами событий, через которые он проходит.

Длина любого пути определяется суммарной продолжительностью составляющих его работ.

Полный путь - это путь от исходного до завершающего события.

В сетевом графике, как правило, имеется несколько полных путей с различной продолжительностью.

Так, для нашего примера имеем пять полных путей, длина которых

L₁(1 - 2 - 5 - 7) = 4 + 5 + 1 = 10;

L₂(1 - 2 - 4 - 7) = 4 + 3 + 3 = 10;

L₃(1 - 2 - 4 - 6 - 7) = 4 + 3 + 3 + 2 = 12;

L₄(1 - 2 - 3 - 6 - 7) = 4 + 1 + 2 + 2 = 9;

L₅(1 - 3 - 6 - 7) = 4 + 2 + 2 = 8.

Полный путь, имеющий максимальную продолжительность, называют критическим путем.

Работы, лежащие на критическом пути, называется критическими работами.

Для нашего примера L_кр (1 - 2 - 4 - 6 - 7) = 12 единиц времени. Для большей наглядности его выделяют двойными или жирными линиями.

Критический путь (L_кр) определяет общую продолжительность выполнения всего комплекса работ.

Полные пути, продолжительность которых меньше L_кр, называются некритичными. У них имеется резерв времени, в пределах которого время выполнения работ может быть увеличено, что не приводит к увеличению общей продолжительности наступления завершающего события.