По виду нормальной картографической сетки

Вспомогательными поверхностями при переходе от эллипсои­да или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.

48 Глава III. Математическая основа карт

Классификация проекций по виду картографической сетки 49

 

Рис. 3.5. Искажения в равновеликой (а), равнопромежуточной (б) и рав­ноугольной (в) цилиндрических проекциях. Размеры и форма эллип­сов искажений характеризуют искажения площадей и углов (форм).

Цилиндрические проекции — проектирование шара (эллипсои­да) ведется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость (рис. 3.6). Если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору (или сечет его по па­раллелям), то проекция называется нормальной (прямой) цилинд­рической. Тогда меридианы нормальной сетки предстают в виде равноотстоящих параллельных прямых, а параллели — в виде пря­мых, перпендикулярных к ним. В таких проекциях меньше всего искажений в тропических и приэкваториальных областях.

Если ось цилиндра расположена в плоскости экватора, то это — поперечная цилиндрическая проекция. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и следовательно, в такой проекции наиболее выгодно изображать территории, вы­тянутые с севера на юг. В тех случаях, когда ось вспомогательного цилиндра расположена под углом к плоскости-экватора, проекция называется косой цилиндрической. Она удобна для вытянутых тер­риторий, ориентированных на северо-запад или северо-восток.

Конические проекции — поверхность шара (эллипсоида) проек­тируется на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость (рис. 3.7). Как и в предыдущем случае, различают нор­мальную (прямую) коническую проекцию, когда ось конуса совпа­дает с осью вращения Земли, поперечную коническую — ось конуса лежит в плоскости экватора и косую коническую — ось конуса на­клонена к плоскости экватора.

В нормальной конической проекции меридианы представляют собой прямые, расходящиеся из точки полюса, а параллели — дуги концентрических окружностей. Воображаемый конус каса­ется земного шара или сечет его в районе средних широт, поэто­му в такой проекции удобнее всего картографировать территории России, Канады, США, вытянутые с запада на восток в средних широтах.

Азимутальные проекции — поверхность земного шара (эллип­соида) переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция (рис. 3.8я). Парал­лели в ней являются концентрическими окружностями, а мериди­аны — радиусами этих окружностей. В этой проекции всегда кар­тографируют полярные области нашей и других планет.

4 - 4886

50 Глава III. Математическая основа карт

Классификация проекций по виду картографической сетки 51

 

а

Рис. 3.6. Цилиндрические проекции.

а — развертка нормальной цилиндрической проекции (проектирование на касательный цилиндр); б ■— нормальная цилиндрическая проекция на секу­щий цилиндр; в — косая цилиндрическая проекция на секущем цилиндре; г— поперечная цилиндрическая проекция на касательном цилиндре (осо­бенно удобна для проектирования геодезических зон).

Рис. 3.7. Нормальная коническая проекция.

а — проекция на касательный конус и развертка; б — проекция на секущий конус и развертка.

Рис. 3.8. Азимутальные проекции.

а — нормальная или полярная проекция на плоскость; б — сетка в полярной проекции; в — сетка в поперечной (экваториальной) проекции; г — сетка в косой азимутальной проекции.

г

52 Глава III. Математическая основа карт

Классификация проекций по виду картографической сетки 53

 

Если плоскость проекции перпендикулярна к плоскости эква­тора, то получается поперечная (экваториальная) азимутальная

проекция. Она всегда используется для карт полушарий (рис. 3.8#). А если проектирование выполнено на касательную или секущую вспомогательную плоскость, находящуюся под любым углом к плоскости экватора, то получается косая азимутальная проекция (рис. 3.8г).

Можно показать, что азимутальные проекции являются пре­дельным случаем конических, когда угол при вершине конуса принимается равным 180°.

Среди азимутальных проекций выделяют несколько их разно­видностей, различающихся по положению точки, из которой ве­дется проектирование шара на плоскость (рис. 3.9).

а б в

 

 

Название азимутальной проекции Гномон ическая Стереографическая Внешняя Ортографическая

Положение точки проектирования относительно шара (эллипсоида)

В центре шара

На противоположном конце

диаметра

Плоскость проектирования

За пределами тара на продол­жении диаметра В бесконечности

Ортографическая

Внешняя Стереографическая

Гномон ическая

Рис. 3.9. Положение центра проектирования для азимутальных проекций.

Рис. ЗЛО. Вид сетки меридианов и параллелей в разных картографических проекциях.

а — цилиндрическая; б — коническая; в — азимутальная; г — псевдоцилин­дрическая; д — псевдоконическая; е — поликоническая, ж — псевдоазиму­тальная.

Условные проекции — проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий, например желательного вида географической сетки, того или иного распределения искажений на карте, задан­ного вида сетки и др. В частности, к условным принадлежат псевдо­цилиндрические, псевдоконические, псевдоазимутиальные и другие про­екции, полученные путем преобразования одной или нескольких исходных проекций. На рис. 3.10 приведены виды сеток описанных выше и некоторых условных проекций.

Псевдоцилиндрические проекции — проекции, в которых парал­лели — прямые линии (как и в нормальных цилиндрических про­екциях), средний меридиан — перпендикулярная им прямая, а остальные меридианы — кривые, увеличивающие свою кривизну по мере удаления от среднего меридиана. Чаще всего эти проекции применяют для карт мира и Тихого океана.

Псевдоконические проекции — такие, в которых все параллели изображаются дугами концентрических окружностей (как в нор­мальных конических), средний меридиан — прямая линия, а ос­тальные меридианы — кривые, причем кривизна их возрастает с

54 Глава III. Математическая основа карт

Классифыкацыя проекций по виду картографической сетки 55

 

 

Рис. 3.11. Принцип построения поликонической проекции. а — положение конусом; б — полосы; в — развертка.

удалением от среднего меридиана. Применяются для карт России, Евразии, других материков.

Поликонические проекции — проекции, получаемые в результа­те проектирования шара (эллипсоида) на множество конусов. В нормальных поликонических проекциях параллели представлены дугами эксцентрических окружностей, а меридианы — кривые, симметричные относительно прямого среднего меридиана (рис. 3.11). Чаще всего эти проекции применяются для карт мира.

Псевдоазимутальные проекции — видоизмененные азимуталь­ные проекции. В полярных псевдоазимутальных проекциях парал­лели представляют собой концентрические окружности, а мери­дианы — кривые линии, симметричные относительно одного или двух прямых меридианов. Поперечные и косые псевдоазимуталь­ные проекции имеют общую овальную форму и обычно применя­ются для карт Атлантического океана или Атлантического океана вместе с Северным Ледовитым.

Многогранные проекции — проекции, получаемые путем про­ектирования шара (эллипсоида) на поверхность касательного или секущего многогранника (рис. 3.12). Чаще всего каждая грань пред-

Рис. 3.12. Схема многогранной проекции и расположение листов карт.

ставляет собой равнобочную трапецию, хотя возможны и иные варианты (например, шестиугольник, квадрат, ромб). Разновид­ностью многогранных являются многополосные проекции, причем полосы могут «нарезаться» и по меридианам, и по параллелям. Такие проекции выгодны тем, что искажения в пределах каждой грани или полосы совсем невелики, поэтому их всегда использу­ют для многолистных карт. Рамка каждого листа, составленного в многогранной проекции, представляет собой трапецию, образо­ванную линиями меридианов и параллелей. За это приходится «рас­плачиваться» — блок листов карт нельзя совместить по общим рамкам без разрывов.

Надо отметить, что в наши дни для получения картографи­ческих проекций не пользуются вспомогательными поверхностя­ми. Никто не помещает шар в цилиндр и не надевает на него конус. Это всего лишь геометрические аналогии, позволяющие понять геометрическую суть проекции. Изыскание проекций вы­полняют аналитически. Компьютерное моделирование позволяет достаточно быстро рассчитать любую проекцию с заданными па­раметрами, автоматические графопостроители легко вычерчива­ют соответствующую сетку меридианов и параллелей, а при необ­ходимости — и карту изокол.

Существуют специальные атласы проекций, позволяющие по­добрать нужную проекцию для любой территории. В последнее время созданы электронные атласы проекций, с помощью которых лег­ко отыскать подходящую сетку, сразу оценить ее свойства, а при необходимости провести в интерактивном режиме те или иные модификации или преобразования.

Глава III. Математическая основа карт

Выбор проекций

 

40 «О W ЮО 120 I40JM

20 0 20 40 60 JO IO0 IM NO W)

Выбор проекций

На выбор проекций влияет много факторов, которые можно сгруппировать следующим образом:

♦ географические особенности картографируемой территории, ее положение на земном шаре, размеры и конфигурация;

♦ назначение, масштаб и тематика карты, предполагаемый круг потребителей;

♦ условия и способы использования карты, задачи, которые будут решаться по ней, требования к точности результатов измерений;

♦ особенности самой проекции — искажения длин, площадей, углов и их распределение по территории, форма меридианов и параллелей, их симметричность, изображение полюсов, кривизна линий кратчайшего расстояния.

Первые три группы факторов задаются изначально, четвертая — зависит от них. Например, указывается, что создается настенная карта России для средней школы — значит, территория расположена в средних широтах, масштаб карты не крупнее 1:4 000 000 — 1:5 000 000. измерения по ней проводиться не будут, но желательно не иметь значительных искажений форм и площадей. При отсутствии каких-либо дополнительных условий скорее всего будет избрана одна из равнопромежуточных конических проекций. Если же составляется карта, предназначенная для навигации, то обязательно должна быть использована равноугольная цилиндрическая проекция Меркатора. Если картографируется Антарктида, то почти наверняка будет при­нята нормальная (полярная) азимутальная проекция и т. д.

Значимость названных факторов может быть различной: в од­ном случае на первое место ставят наглядность (например, для настенной школьной карты), в другом — особенности использо­вания карты (навигация), в третьем — положение территории на земном шаре (полярная область). Возможны любые комбинации, а следовательно, и разные варианты проекций, тем более что выбор очень велик. Но все же можно указать некоторые предпочтитель­ные и наиболее традиционные проекции.

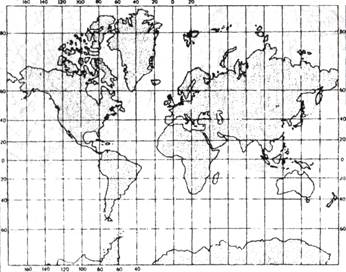
Карты мира обычно составляют в цилиндрических, псевдоци­линдрических и поликонических проекциях (рис. 3.13). Для умень­шения искажений часто используют секущие цилиндры, а псевдо­цилиндрические проекции иногда дают с разрывами на океанах.

Рис. 3.13. Примеры проекций для карт мира.

а — цилиндрическая проекция Меркатора; б — псевдоцилиндрическая про­екция Мольвейде.

44�1554444

58 Глава III Математическая основа карт

Выбор проекций

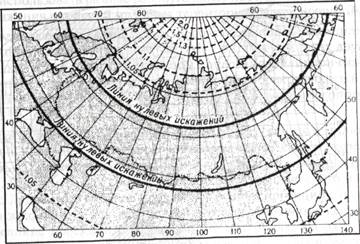
Рис. 3.14. Проекции для карт полушарий.

а — поперечная азимутальная орфографическая проекция для восточного полушария; б — нормальная равпопромежуточная проекция Постеля для се­верного полушария.

Карты полушарий всегда строят в азимутальных проекциях. Для западного и восточного полушарий естественно брать поперечные (экваториальные), для северного и южного полушарий — нормаль­ные (полярные) (рис. 3.14), а в других случаях (например, для материкового и океанического полушарий) — косые азимуталь­ные проекции.

Карты материков: Европы, Азии, Северной и Южной Амери­ки, Австралии с Океанией чаще всего строят в равновеликих ко­сых азимутальных проекциях, для Африки берут поперечные, а для Антарктиды — нормальные азимутальные проекции.

Карты России в целом составляют чаще всего в нормальных конических равнопромежуточных проекциях с секущим конусом, но в некоторых особых случаях — в поликонических, произволь­ных и др. На рис. 3.15 показана наиболее часто употребляемая сетка конической проекции, которая, однако, в некоторых случаях ока­зывается не совсем удобной. Например, для карты начальной школы проекция должна быть построена так, чтобы самая северная точка России располагалась ближе всего к северной рамке, а Черное море находилось возле южной, а не западной рамки карты.

Карты отдельных стран, административных областей, про­винций, штатов выполняют в косых равноугольных и равнове-

Рис. 3.15. Проекции для карт России и сопредельных государств.

/- нормальная равпопромежуточная проекция Каврайского; б - попереч--цилиндрическая проекция Соловьева. На обе сетки нанесены изоколы

но-площадей.

ликих конических или азимутальных проекциях, но многое зависит от конфигурации территории и ее положения на земном шаре. Для небольших районов задача выбора проекции теряет актуальность,

Глава III. Математическая основа карт

Распознавание проекций 61

 

Рис. 3.16. Проекции с разрывами.

а — разрывы изображения в пределах океана (для уменьшения искажений на материках); б — разрывы изображения в пределах материков (для сохранения равновеликости океанов).

можно использовать разные равноугольные проекции, имея в виду, что искажения площадей на малых территориях почти неощутимы.

Топографические карты в России создают в поперечно-цилин­дрической проекции Гаусса—Крюгера, а в США и многих других западных странах — в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно UTM). Обе проекции близки по своим свойствам, и та и другая по существу являются многополос­ными.

Морские и аэронавигационные карты всегда даются в цилинд­рической проекции Меркатора, а тематические карты морей и океанов— в самых разнообразных, иногда довольно сложных про­екциях. Например, для совместного показа Атлантического и Се­верного Ледовитого океанов применяют особые проекции с оваль­ными изоколами, а для изображения всего Мирового океана — равновеликие проекции с разрывами на материках. На рис. 3.16 представлены две сетки в разорванных проекциях. Одна имеет раз­рывы на океанах и предназначена для картографирования явлений, расположенных только на суше, а в другой разрывы сделаны на ма­териках. Она выглядит непривычно и состоит как бы из трех лепест­ков: Тихий океан, Атлантический вместе с Северным Ледовитым и Индийский. Разрывы на материках даны для того, чтобы оставить без искажений площади океанов и проводить по ним измерения.

В любом случае при выборе проекции, в особенности для тема­тических карт, следует иметь в виду, что обычно искажения на карте минимальны в центре и быстро возрастают к краям. Кроме того, чем мельче масштаб карты и обширнее пространственный охват, тем больше внимания приходится уделять «математичес­ким» факторам выбора проекции, и наоборот — для малых терри­торий и крупных масштабов более существенными становятся гео­графические факторы.

Распознавание проекций

Распознать проекцию, в которой составлена карта, — значит, установить ее название, определить принадлежность к тому или иному виду, классу. Это нужно для того, чтобы иметь представле­ние о свойствах проекции, характере, распределении и величине искажений — словом, для того чтобы знать, как пользоваться кар­той, чего от нее можно ожидать.

9462 Глава III. Математическая основа карт

Координатные сетки

 

Некоторые нормальные проекции сразу распознаются по виду меридианов и параллелей. Например, легко узнаваемы нормаль­ные цилиндрические, псевдоцилиндрические, конические, ази­мутальные проекции. Но даже опытный картограф не сразу рас­познает многие произвольные проекции, потребуются специаль­ные измерения по карте, чтобы выявить их равноугольность, равновеликость или равнопромежуточность по одному из направ­лений. Для этого существуют особые приемы: сперва устанавлива­ют форму рамки (прямоугольник, окружность, эллипс), опреде­ляют, как изображены полюсы, затем измеряют расстояния меж­ду соседними параллелями вдоль по меридиану, площади соседних клеток сетки, углы пересечения меридианов и параллелей, харак­тер их кривизны и т.п.

Существуют специальные таблицы-определители проекций для карт мира, полушарий, материков и океанов. Проведя необходимые измерения по сетке, можно отыскать в такой таблице название про­екции. Это даст представление о ее свойствах, позволит оценить воз­можности количественных определений по данной карте, выбрать соответствующую карту с изоколами для внесения поправок.

Координатные сетки

Координатные сетки — важный элемент математической ос­новы карт. Они необходимы для ориентирования по карте, опре­деления направлений (азимутов, румбов, дирекционных углов), прокладки маршрутов, нанесения элементов содержания, новых объектов по их координатам и снятия с карты координат объектов. Кроме того, наличие сетки позволяет судить о масштабе карты, виде проекции и распределении искажений в ней. Сетка делает карту картой, говорят даже, что «карта без сетки все равно что термометр без шкалы». На картах используют разные координат­ные сетки.

Картографическая сетка — это изображение на карте линий меридианов и параллелей {географической сетки), отражающих значения долгот, счет которых ведется от начального Гринвичско­го меридиана, и широт, которые отсчитываются от экватора (рис. 3.17). Картографическая сетка имеет важный географический смысл, она показывает направления «север — юг» и «запад — вос­ток», позволяет судить о широтных поясах, о расположении объек­тов относительно стран света. От северного направления меридиа-

Плоскость начального меридиана

Рис. 3.17. Широта (ср) и долгота (К) точки А на глобусе и сетка паралле­лей и меридианов на карте.

на по часовой стрелке отсчитываются географические азимуты, а разность долгот двух пунктов выражает разность их времени. На картах линии географической сетки наносят обычно через равные интервалы: несколько десятков градусов, несколько градусов, минут и даже секунд — все зависит от масштаба и назначения карты.

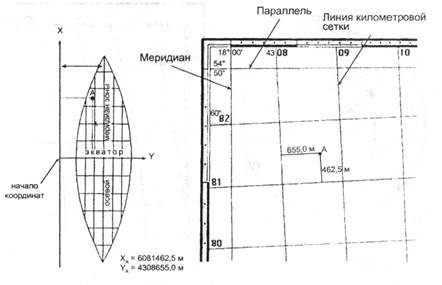
Сетка прямоугольных координат (прямоугольная сетка) — стан­дартная система взаимно перпендикулярных линий, проведенных через равные расстояния, например через определенное число километров (отсюда название километровая сетка, или сетка ки­лометровых квадратов). Обычно эта сетка наносится на топографи­ческие карты и планы, ее вертикальные линии идут параллельно осевому меридиану геодезической зоны (ось абсцисс), а горизон­тальные — параллельно экватору (ось ординат); они оцифрованы через километр, а километровая рамка карты имеет более дробные деления (рис. 3.18). Такая сетка удобна для геодезических вычисле­ний: определения прямоугольных координат, расстояний, дирек­ционных углов и т.п.

Сетка-указателъница — любая сетка на карте, предназначен­ная для указания местоположения и поиска объектов. Ячейки та­кой сетки обозначаются буквами и цифрами (допустим, В-3), и

64 Глава III. Математическая основа карт

Разграфка, номенклатура и рамки карты

 

 

	II	III	IV	V	VI
					XII
	XX
					ххх\л
31° 32° 33° 34° 35° |

36° 00'

56° -00' 55° 20' 54° 40" 54° 00' 53° 20' 52° 40' _52° 00*

52° 00''

36° 00'

1:200 000 N-36-XX

36° 00'

30° 00'

Рис. 3.18. Изображение геодезической зоны с координатными линиями и сетка прямоугольных координат (километровая сетка) на топогра­фической карте.

это удобно, например, для отыскания населенных пунктов по их названиям, содержащимся в алфавитном географическом указа­теле. Обычно сетки-указательницы наносятся на карты атласов, а в конце приводится список названий всех объектов, помещенных в атласе.

Можно встретить и иные координатные сетки. На старинных морских картах — портоланах изображалась сетка компасных ли­ний, на некоторых французских картах до сих пор дается сетка градов (окружность составляет 400 градов, а каждый град содер­жит 100 градовых минут). Некоторые страны используют собствен­ные системы прямоугольных координат и соответственно — свои координатные сетки.