

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Положим теперь, что участок цепи содержит конденсатор емкости 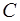 , причем сопротивлением и индуктивностью можно пренебречь. Выясним, по какому закону будет изменяться напряжение на концах участка цепи в этом случае. Полагаем, что сила тока изменяется по закону
, причем сопротивлением и индуктивностью можно пренебречь. Выясним, по какому закону будет изменяться напряжение на концах участка цепи в этом случае. Полагаем, что сила тока изменяется по закону 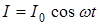 .
.
Напряжение на конденсаторе равно
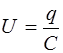 . (6.4)
. (6.4)
Ток можно записать через величину заряда 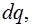 протекающего через сечение проводника и увеличивающего заряд конденсатора за промежуток времени
протекающего через сечение проводника и увеличивающего заряд конденсатора за промежуток времени 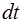
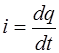 . (6.5)
. (6.5)
Тогда заряд конденсатора можно найти интегрированием
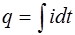 . (6.6)
. (6.6)
Поскольку сила тока в цепи изменяется по закону
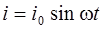 , (6.7)
, (6.7)
то заряд равен
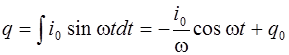 . (6.8)
. (6.8)
Постоянная интегрирования 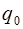 здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим
здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим 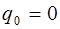 . Следовательно, с учетом формулы (6.4) можно записать для напряжения
. Следовательно, с учетом формулы (6.4) можно записать для напряжения
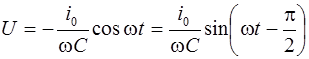 (6.9)
(6.9)
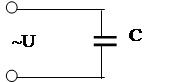 |
Рисунок 6.4 Рисунок 6.5
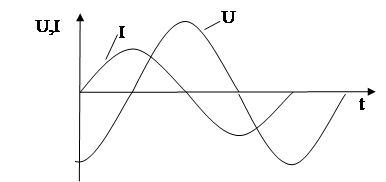
Сравнение выражений (6.7) и (6.9) показывает, что при гармонических колебаниях тока в цепи напряжение на конденсаторе изменяется также по гармоническому закону, однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на 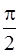
Изменение тока и напряжения во времени изображено графически на рисунке 6.5.
Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой – либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому колебания напряжения, как и колебания заряда, запаздывают относительно колебаний тока. Так, например, когда в момент времени 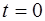 сила тока равна нулю (рисунок 6.5), то на пластинах конденсатора еще имеется заряд, перенесенный током в предыдущий промежуток времени, и напряжение не равно нулю. Для обращения в нуль этого заряда нужно, чтобы в течение промежутка времени, равного
сила тока равна нулю (рисунок 6.5), то на пластинах конденсатора еще имеется заряд, перенесенный током в предыдущий промежуток времени, и напряжение не равно нулю. Для обращения в нуль этого заряда нужно, чтобы в течение промежутка времени, равного 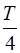 , проходил ток положительного направления. Однако, когда заряд конденсатора (а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю (рисунок 6.5)–она принимает максимальное значение.
, проходил ток положительного направления. Однако, когда заряд конденсатора (а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю (рисунок 6.5)–она принимает максимальное значение.
Формула (6.9) показывает, что амплитуда напряжения на конденсаторе равна
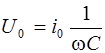 . (6.10)
. (6.10)
Сравнивая это выражение с законом Ома для участка цепи постоянного тока 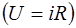 , мы видим, что величина
, мы видим, что величина
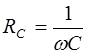 , (6.11)
, (6.11)
зависящая от емкости конденсатора 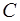 , играет роль сопротивления участка цепи. Поэтому она получила название кажушегося сопротивления емкости или емкостным сопротивлением. Емкостное сопротивление равно отношению амплитуды напряжения на емкости к амплитуде силы тока в цепи. В Международной системе единиц СИ емкостное сопротивление выражается в омах.
, играет роль сопротивления участка цепи. Поэтому она получила название кажушегося сопротивления емкости или емкостным сопротивлением. Емкостное сопротивление равно отношению амплитуды напряжения на емкости к амплитуде силы тока в цепи. В Международной системе единиц СИ емкостное сопротивление выражается в омах. 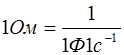 . Емкостное сопротивление равно величине, обратной произведению электрической емкости ( в
. Емкостное сопротивление равно величине, обратной произведению электрической емкости ( в 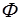 ) и циклической частоты переменного тока
) и циклической частоты переменного тока 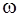 (в
(в 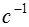 ).
).
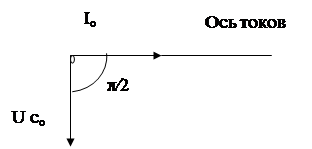 Полученные результаты можно представить в виде векторной диаграммы (рисунок 6.6). Здесь вектор, изображающий колебания напряжения, уже не совпадает с осью токов. Он повернут в отрицательном направлении (по часовой стрелке) на угол
Полученные результаты можно представить в виде векторной диаграммы (рисунок 6.6). Здесь вектор, изображающий колебания напряжения, уже не совпадает с осью токов. Он повернут в отрицательном направлении (по часовой стрелке) на угол 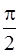 . Модуль этого вектора равен амплитуде напряжения
. Модуль этого вектора равен амплитуде напряжения 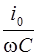 .
.
Рисунок 6.6
Из формулы (6.11) видно, что сопротивление емкости 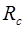 зависит также от частоты
зависит также от частоты 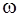 . Поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.
. Поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!