

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Цели работы:
1. Ознакомление с работой вискозиметра Оствальда и медицинского вискозиметра.
2. Определение коэффициента вязкости жидкости.
Теоретические сведения
Течение реальной жидкости по трубе постоянного сечения сопровождается падением статического давления. Это явление объясняется наличием у жидкости внутреннего трения (вязкости) и сопровождается переходом части ее механической энергии во внутреннюю. При ламинарном течении жидкости по трубе скорость слоев непрерывно меняется от максимальной (по оси трубы) до нуля (у стенок).
Любой из слоев тормозит движение соседнего слоя, расположенного ближе к оси трубы, и оказывает ускоряющее действие на слой, расположенный дальше от оси.
Между соприкасающимися слоями жидкости действуют касательные силы внутреннего трения. Модуль этих сил зависит от площади S слоев и градиента скорости dV/dx (изменения скорости на единицу длины в направлении, перпендикулярном скорости) и определяется законом Ньютона:
F=η(dV/dx)S, (3.1)
где η – динамический коэффициент вязкости, численно равный силе трения, возникающей между параллельно движущимися слоями жидкости единичной площади при единичном градиенте скорости.
В системе СИ за единицу вязкости принимается вязкость жидкости, у которой сила трения между двумя соприкасающимися слоями, рассчитанная на единицу площади (1 квадратный метр), равна одному Ньютону при градиенте скорости 1 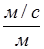 или 1
или 1 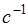 .
.
Единица вязкости в СИ – паскаль-секунда ( 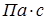 ):
):
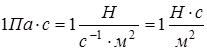 =1
=1 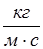
Для единицы вязкости в системе СГС установлено название “пуаз” ( 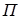 ).
).
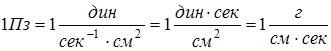 .
.
Вязкостью в один пуаз обладает жидкость, у которой сила трения между двумя соседними слоями, рассчитанная на 1 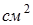 площади соприкосновения слоев при градиенте скорости 1
площади соприкосновения слоев при градиенте скорости 1 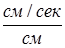 , равна одной дине:
, равна одной дине:
Легко видеть, что 1 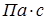 =10
=10 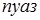 =10
=10 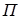
1 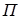 = 1
= 1 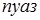 =0,1
=0,1 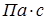 .
.
На практике часто употребляется в сто раз меньшая единица вязкости – сантипуаз. Примерно такую вязкость имеет вода при 200С.
1 сантипуаз = 10-2 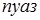 =10-3
=10-3 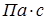 .
.
Вязкость других жидкостей имеет разнообразные значения. Вязкость этилового спирта при 200С равна 1,2 сантипуаза, этилового эфира – около 0,2 сантипуаза. Глицерин имеет вязкость 850 сантипуазов при температуре 200С и 350 сантипуазов при 300С.
Вязкость некоторых жидкостей (эмульсии, суспензии, растворы полимеров) зависит от режима их течения – давления, градиента скорости. Это объясняется тем, что структурные элементы жидкости (белковые молекулы, дисперсные частицы) располагаются в потоке по-разному при разных скоростях. Такие жидкости называют неньютоновскими. Кровь (суспензия клеток крови в белковом растворе – плазме) также относится к неньютоновским жидкостям.
При течении жидкости по трубке, стенки которой смачиваются ею, можно считать, что слой жидкости, непосредственно прилегающий к внутренней поверхности трубки, прилипает к ней и остается неподвижным. Более удаленные от стенок слои скользят вдоль соседних слоев, и скорость движения жидкости возрастает по мере удаления от стенок. С наибольшей скоростью движутся частицы жидкости, находящиеся на оси трубки.
Рассмотрим стационарный поток жидкости, ламинарно текущей слева направо через трубку круглого сечения, радиус которой 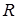 (рисунок 3.1).
(рисунок 3.1).
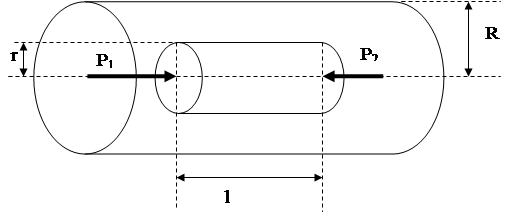 |
Рисунок 3.1
Мысленно выделим в жидкости цилиндр радиуса 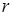 и длины
и длины 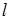 , ось которого совпадает с осью трубки. Обозначим давление на его торцах через
, ось которого совпадает с осью трубки. Обозначим давление на его торцах через 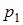 и
и 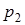 . В стационарных условиях результирующая сил давления на основания цилиндра
. В стационарных условиях результирующая сил давления на основания цилиндра 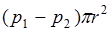 уравновешивается силой вязкого трения, действующей на боковую поверхность цилиндра со стороны наружных слоев жидкости. По закону вязкого трения эта сила равна:
уравновешивается силой вязкого трения, действующей на боковую поверхность цилиндра со стороны наружных слоев жидкости. По закону вязкого трения эта сила равна:
 , (3.2)
, (3.2)
где 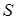 – площадь боковой поверхности цилиндра,
– площадь боковой поверхности цилиндра,
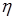 – динамическая вязкость жидкости,
– динамическая вязкость жидкости,
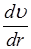 – градиент скорости.
– градиент скорости.
Заменяя 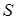 через площадь боковой поверхности
через площадь боковой поверхности 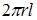 и приравнивая нулю сумму сил, действующих на цилиндр, можно записать:
и приравнивая нулю сумму сил, действующих на цилиндр, можно записать:
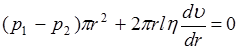 . (3.3)
. (3.3)
Откуда выразим 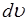 :
:
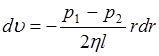 . (3.4)
. (3.4)
Знак “–“ в формуле (3.4) свидетельствует о том, что с увеличением расстояния от оси трубки скорости частиц жидкости уменьшаются ( 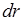 >0,
>0, 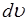 <0).
<0).
Интегрируя, получим функцию 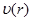 :
:
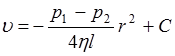 , (3.5)
, (3.5)
где С – константа интегрирования, которая может быть найдена из граничных условий. Чтобы найти ее, заметим, что скорость жидкости обращается в нуль на внутренней поверхности трубки, где жидкость “прилипает” к стенкам, т.е. 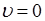 при
при 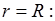
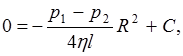 (3.6)
(3.6)
откуда 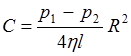 . (3.7)
. (3.7)
Таким образом, зависимость скорости частиц жидкости от расстояния до оси трубки 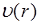 имеет вид:
имеет вид:
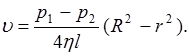 (3.8)
(3.8)
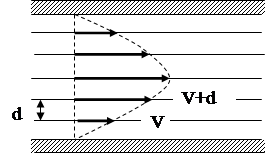 |
Рисунок 3.2
Как следует из полученной функции (3.8), скорость жидкости квадратично меняется с радиусом 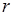 и максимальна на оси трубки при
и максимальна на оси трубки при 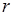 =0 (рисунок 3.2 ). Максимальная скорость частиц жидкости равна:
=0 (рисунок 3.2 ). Максимальная скорость частиц жидкости равна:
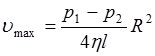 . (3.9)
. (3.9)
Объем жидкости, протекающей через кольцевое поперечное сечение трубки радиуса 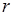 с величиной зазора
с величиной зазора 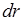 (рисунок 3.3) за промежуток времени
(рисунок 3.3) за промежуток времени 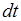 ,равен:
,равен:
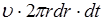 , (3.10)
, (3.10)
а за единицу времени
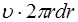 . (3.11)
. (3.11)
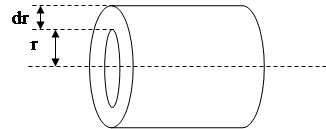 |
Рисунок 3.3
Объем жидкости, протекающей за единицу времени через все поперечное сечение трубки, можно получить, проинтегрировав последнее выражение от нуля до радиуса трубки R:
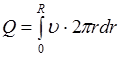 . (3.12)
. (3.12)
Подставив функцию 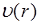 в (3.12), получим:
в (3.12), получим:
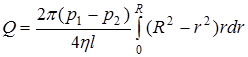 , (3.13)
, (3.13)
откуда
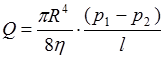 . (3.14)
. (3.14)
Полученное выражение носит название формулы Пуазейля. Величину Q называют объемной скоростью истечения жидкости или газа. Единица измерения объемной скорости истечения в СИ метр кубический на секунду (м3/с).
Прежде чем применять формулу Пуазейля к конкретным расчетам, всегда следует убедиться в том, что течение жидкости является ламинарным.
В реальной жизни мы редко встречаемся с ламинарным течением. Движение воды в водопроводе и в реке, движение воздуха в атмосфере практически всегда оказывается турбулентным. Разделить эти два режима можно, исследуя зависимость объемной скорости истечения от давления. При ламинарном течении объемная скорость пропорциональна разности давлений 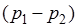 на концах трубки:
на концах трубки:
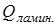 ~
~ 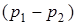 , (3.15)
, (3.15)
а при турбулентном – корню квадратному из нее:
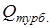 ~
~ 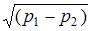 . (3.16)
. (3.16)
Характер течения жидкости зависит от числа Рейнольдса Re, которое определяется с помощью формулы:
Re = 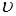
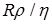 , (3.17)
, (3.17)
где 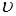 – скорость потока,
– скорость потока, 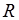 – радиус трубки,
– радиус трубки, 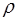 – плотность жидкости,
– плотность жидкости, 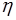 – динамический коэффициент вязкости жидкости. В гладких трубках круглого сечения течение имеет ламинарный характер, если Re <1000.
– динамический коэффициент вязкости жидкости. В гладких трубках круглого сечения течение имеет ламинарный характер, если Re <1000.
Ламинарное движение жидкости при переходе ее из широкого сосуда в капилляр устанавливается не сразу, а после того, как она пройдет расстояние a, зависящее от радиуса трубки и числа Рейнольдса:
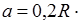 Re. (3.18)
Re. (3.18)
Приборы, служащие для определения вязкости, называются вискозиметрами. В данной работе вязкость жидкости определяется при помощи капиллярного вискозиметра.
Вязкость жидкостей может быть определена абсолютным методом, т.е. путем непосредственного измерения линейных размеров капилляра, объема жидкости и времени ее истечения. Чтобы, пользуясь формулой Пуазейля, определить коэффициент вязкости жидкости 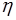 , надо иметь возможность с большой точностью измерить все величины, входящие в формулу (3.14), что сделать довольно трудно.
, надо иметь возможность с большой точностью измерить все величины, входящие в формулу (3.14), что сделать довольно трудно.
Значительно проще относительный метод. В этом случае вязкость исследуемой жидкости может быть определена путем ее сравнения с известным коэффициентом вязкости другой жидкости. Относительный метод измерения вязкости является более распространенным. В этом случае нужно лишь измерить промежутки времени 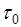 и
и 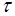 протекания через одну и ту же капиллярную трубку строго одинакового объема двух жидкостей с коэффициентами вязкости
протекания через одну и ту же капиллярную трубку строго одинакового объема двух жидкостей с коэффициентами вязкости 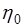 (известным) и
(известным) и 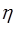 (подлежащим определению).
(подлежащим определению).
3.2 Вискозиметр Оствальда
Вискозиметр Оствальда (рисунок 3.4) представляет собой U-образную стеклянную трубку, в одно колено которой впаян капилляр 1 с шариком 2 в верхней части. Выше шарика поставлена метка “а”, ниже шарика – метка “b”. Внутренний объем шарика между метками равен 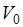 .
.
Другое колено вискозиметра представляет собой широкую трубку 3. Внизу находится резервуар 4, в который через широкую трубку заливают из бюретки определенный объем дистиллированной воды, вязкость которой известна. 

С помощью резиновой груши, подсоединенной к широкой трубке вискозиметра, воду из резервуара поднимают по капилляру так, чтобы ее мениск установился несколько выше метки “а” (либо жидкость всасывается через капиллярную трубку). Сняв грушу с трубки и удерживая вискозиметр в вертикальном положении, дают возможность воде свободно протекать через капилляр, наблюдая за понижением уровня жидкости. Когда мениск проходит мимо верхней метки “а”, включают секундомер и выключают его, когда мениск проходит мимо нижней метки “b”. Таким образом измеряют время 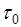 , за которое объем
, за которое объем 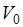 эталонной жидкости протекает через капилляр.
эталонной жидкости протекает через капилляр.
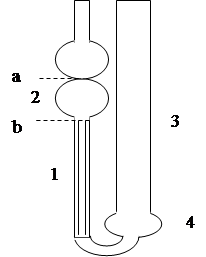 |
Рисунок 3.4
В капиллярном вискозиметре диаметр капилляра и перепад давления на нем подобраны так, что течение жидкости в капилляре всегда является ламинарным.
Для расчета процесса течения эталонной жидкости через капилляр воспользуемся формулой Пуазейля. Разность давлений 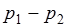 на концах капилляра в вискозиметре Оствальда
на концах капилляра в вискозиметре Оствальда

 P1-P2=ρgh, (3.19)
P1-P2=ρgh, (3.19)
где ρ – плотность жидкости, g– ускорение свободного падения.
С учетом сказанного формула Пуазейля в применении к жидкости, протекающей по капилляру вискозиметра, принимает вид:
V=πR4ρghτ/8ηl, (3.20)
где 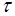 – промежуток времени протекания через капилляр вискозиметра исследуемой жидкости, плотность которой
– промежуток времени протекания через капилляр вискозиметра исследуемой жидкости, плотность которой 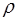 , а вязкость
, а вязкость 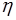 .
.
Для эталонной жидкости:
V=πR4ρ0 ghτ0 /8η0 l (3.21)
Приравнивая друг к другу правые части выражений (3.20) и (3.21), получаем после сокращения:
r0t0/h0=rt/h. (3.22)
Зная коэффициент внутреннего трения h0 одной жидкости, легко найти коэффициент внутреннего трения 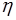 другой жидкости, если известны r0,
другой жидкости, если известны r0, 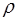 , а также t0,
, а также t0, 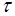 .
.
h=h0rt/r0t0 (3.23)
Эта формула является окончательной. Плотность воды при различных температурах приведена в таблице 1 приложения. Значение вязкости дистиллированной воды при комнатной температуре следует взять из таблицы 2 приложения.
Приложение
Таблица 1. Плотность воды при различных температурах.
| t,0C | ρ0, г/см3 | t,0C | ρ0 ,г/см3 |
| 0 | 0,99987 | 15 | 0,99913 |
| 1 | 0,99993 | 16 | 0,99897 |
| 2 | 0,98997 | 17 | 0,99880 |
| 3 | 0,99999 | 18 | 0,99862 |
| 4 | 1,00000 | 19 | 0,99843 |
| 5 | 0,99999 | 20 | 0,99823 |
| 6 | 0,99997 | 21 | 0,99802 |
| 7 | 0,99993 | 22 | 0,99780 |
| 8 | 0,99988 | 23 | 0,99757 |
| 9 | 0,99981 | 24 | 0,99732 |
| 10 | 0,99973 | 25 | 0,99707 |
| 11 | 0,99963 | 26 | 0,99681 |
| 12 | 0,99952 | 27 | 0,99654 |
| 13 | 0,99940 | 28 | 0,99626 |
| 14 | 0,99927 | 29 | 0,99597 |
Таблица 2 Вязкость воды в интервале температур 0 – 1000С
| Температура, 0С | Вязкость 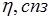
| Температура, 0С | Вязкость 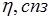
|
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 92 93 94 95 96 | 1,7921 1,7313 1,6728 1,6191 1,5674 1,5188 1,4728 1,4284 1,3860 1,3462 1,3077 1,2713 1,2363 1,2028 1,1709 1,1404 1,1111 1,0828 1,0559 1,0299 1,0050 0,9810 0,9579 0,9358 0,9142 0,8937 0,8737 0,8545 0,8360 0,8180 0,8007 0,7840 0,7679 0,7523 0,7371 0,7225 0,7085 0,6947 0,6814 0,6685 0,6560 0,6439 0,6321 0,6207 0,6097 0,5988 0,3095 0,3060 0,3027 0,2994 0,2962 | 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 97 98 99 100 | 0,5883 0,5782 0,5683 0,5588 0,5494 0,5404 0,5315 0,5229 0,5146 0,5064 0,4985 0,4907 0,4832 0,4759 0,4688 0,4618 0,4550 0,4483 0,4418 0,4355 0,4293 0,4233 0,4174 0,4117 0,4061 0,4006 0,3952 0,3900 0,3849 0,3799 0,3750 0,3702 0,3655 0,3610 0,3565 0,3521 0,3478 0,3436 0,3395 0,3355 0,3315 0,3276 0,3239 0,3202 0,3195 0,3130 0,2930 0,2899 0,2868 0,2838 |
Коэффициент вязкости жидкости зависит от температуры, и поэтому необходимо указывать температуру, при которой он был получен.
3.3 Приборы и принадлежности: вискозиметр Оствальда, дистиллированная вода, исследуемая жидкость, секундомер, резиновая груша.
Порядок выполнения работы
1. При комнатной температуре определите продолжительность протекания через капилляр вискозиметра объема дистиллированной воды, заключенного между метками “а” и “b”. Повторите измерения три раза.
2. Определите плотность воды 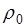 и коэффициент вязкости воды η0 при комнатной температуре, а также плотность исследуемой жидкости ρ.
и коэффициент вязкости воды η0 при комнатной температуре, а также плотность исследуемой жидкости ρ.
3. .Определите продолжительность протекания через капилляр вискозиметра объема исследуемой жидкости, заключенного между метками “а” и “b”. Повторите измерения три раза. Результаты занесите в таблицу 3.1.
Таблица 3.1
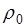 , кг/м3 , кг/м3
| ρ, кг/м3 | η0, Па с | η, Па с | Δη, Па с | τ0, с | τ, с |
4.Вычислите коэффициент вязкости исследуемой жидкости по формуле:
h=h0rt/r0t0
5. Рассчитайте относительную и абсолютную погрешности коэффициента динамической вязкости:
e= Δt/t+ Δt0/t0+ Δr0/r0+ Δr/r+ Δh0/h0 (3.24)
Δh=he (3.25)
Контрольные вопросы
1. Что такое сила внутреннего трения?
2. Напишите уравнение Ньютона для течения вязкой жидкости.
3. Как зависит вязкость жидкости от температуры?
4. Выведите формулу Пуазейля.
5. Выведите формулу для определения вязкости жидкости методом Оствальда.
6. Опишите устройство и принцип работы медицинского вискозиметра.
Техника безопасности
Вискозиметр Оствальда изготовлен из стекла, поэтому следует быть осторожными.
|
|
|

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!