Цель работы: определение коэффициента поверхностного натяжения жидкости методом отрыва капель.
Перед выполнением лабораторной работы следует ознакомиться с содержанием параграфов 4.1 и 4.2 настоящего пособия.
Описание метода
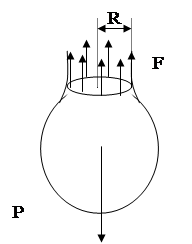
Для определения поверхностного натяжения в медицинской практике пользуются методом отрыва капель. При медленном истечении жидкости из отверстия или вертикальной трубки образуется капля (рис.10). Отрыв происходит по шейке капли или перетяжке, радиус которой меньше радиуса отверстия. Предполагается, что в момент отрыва сила поверхностного натяжения F=2πRσ равна силе тяжести P=ρgV капли (R – радиус шейки капли, ρ – плотность жидкости, V – объем капли ), т.е. 2πRσ=ρgV, откуда :
σ=ρgV/2πR. (5.1) Рисунок 5.1
Измерить радиус шейки капли практически нельзя (это можно сделать только при фотографировании капли в момент отрыва), поэтому, используя метод отрыва капли, прибегают к сравнительному способу.
Если известно поверхностное натяжение σо стандартной жидкости, например, воды, то можно записать:
σо =ρоgVо/2πR. (5.2)
Взяв одинаковые объемы воды и исследуемой жидкости V1 и подсчитав количество капель в этих объемах, можно вычислить объем одной капли:
Vо =V1 /nо (воды), V=V1 /n (исследуемой жидкости).
Подставив эти выражения в формулы (5.1) и (5.2) соответственно, получим:
σ=ρgV/2πRn и σо =ρоgVо/2πRnо.
Тогда σ/σо =ρnо /ρо n или
σ = σо ρnо/ρо n. (5.3)
Описание установки
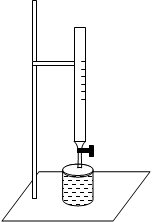 Установка для определения поверхностного натяжения методом отрыва капель (рисунок 5.2) представляет собой укрепленную на вертикальном штативе капельницу. Капельница – это стеклянная трубка с узким нижним концом. На трубке нанесены деления, позволяющие измерять объем протекающей жидкости.
Установка для определения поверхностного натяжения методом отрыва капель (рисунок 5.2) представляет собой укрепленную на вертикальном штативе капельницу. Капельница – это стеклянная трубка с узким нижним концом. На трубке нанесены деления, позволяющие измерять объем протекающей жидкости.
Рисунок 5.2
5.3 Приборы и принадлежности: установка для определения коэффициента поверхностного натяжения методом отрыва капель, исследуемая жидкость.
Порядок выполнения работы
1. Промойте капельницу, закрепите ее вертикально в штативе и залейте в нее определенный объем дистиллированной воды.
2. Открыв кран, подсчитайте число nо капель воды в данном объеме. Опыт проведите три раза, определите среднее значение nо.
3. Залейте в капельницу такой же объем исследуемой жидкости и подсчитайте число капель n в данном объеме. Опыт проведите три раза и рассчитайте среднее значение n.
4. По формуле σ = σо· ρnо/ρо ·n определите поверхностное натяжение исследуемой жидкости.
Контрольные вопросы
1. В чем заключается явление поверхностного натяжения?
2. Что такое сила поверхностного натяжения и как она направлена?
3. Что такое поверхностно-активные вещества?
4. В чем заключается измерение поверхностного натяжения методом отрыва капель?
5. Как зависит поверхностное натяжение от температуры?
6. Какое значение имеет изучение поверхностного натяжения для медицины?
Техника безопасности
Следует соблюдать осторожность при работе со стеклом.
Лабораторная работа. ИЗМЕРЕНИЕ ИНДУКТИВНОСТИ И ЕМКОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Цель работы: изучение цепей переменного тока с активным, емкостным и индуктивным сопротивлением.
Теоретические сведения
Рассмотрим электрические колебания, возникающие в цепи, где имеется генератор, электродвижущая сила которого изменяется периодически. Они подобны вынужденным периодическим колебаниям тела, которые вызываются периодической внешней силой.
Мы ограничимся только цепями с сосредоточенными емкостями и индуктивностями и будем считать переменные токи квазистационарными. Иными словами, мы будем предполагать, что промежуток времени τ, в течение которого электрические величины принимают установившиеся значения, мал по сравнению с периодом колебаний 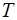 , и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.
, и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.
Далее, мы будем рассматривать только такие токи, мгновенные значения которых 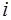 изменяются во времени
изменяются во времени 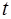 по гармоническому закону (синусоидальному или косинусоидальному):
по гармоническому закону (синусоидальному или косинусоидальному):
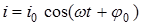 , (6.1)
, (6.1)
где 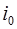 – амплитуда силы тока,
– амплитуда силы тока,
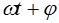 0–фаза колебаний,
0–фаза колебаний,
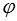 0–начальная фаза,
0–начальная фаза,
ω–циклическая частота, связанная с периодом колебаний 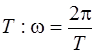 .
.
Это объясняется несколькими причинами. Во–первых, все технические генераторы переменного тока имеют э.д.с., изменяющуюся по закону, очень близкому к гармоническому, и потому создаваемые ими токи практически являются синусоидальными. Вторая причина заключается в том, что теория синусоидальных токов проста, и поэтому на примере таких токов можно выяснить основные особенности электрических колебаний.
Наконец, везде в дальнейшем мы будем считать, что колебания являются установившимися. Иными словами, будем предполагать, что с момента начала колебаний прошло достаточно большое время, так что амплитуды тока и напряжения уже достигли постоянного значения.






 Установка для определения поверхностного натяжения методом отрыва капель (рисунок 5.2) представляет собой укрепленную на вертикальном штативе капельницу. Капельница – это стеклянная трубка с узким нижним концом. На трубке нанесены деления, позволяющие измерять объем протекающей жидкости.
Установка для определения поверхностного натяжения методом отрыва капель (рисунок 5.2) представляет собой укрепленную на вертикальном штативе капельницу. Капельница – это стеклянная трубка с узким нижним концом. На трубке нанесены деления, позволяющие измерять объем протекающей жидкости.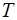 , и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.
, и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.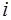 изменяются во времени
изменяются во времени 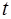 по гармоническому закону (синусоидальному или косинусоидальному):
по гармоническому закону (синусоидальному или косинусоидальному):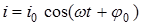 , (6.1)
, (6.1)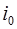 – амплитуда силы тока,
– амплитуда силы тока,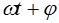 0–фаза колебаний,
0–фаза колебаний,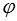 0–начальная фаза,
0–начальная фаза,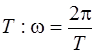 .
.


