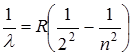(Юстировка производится только лаборантом или преподавателем).
Передвигая окуляр зрительной трубы, добейтесь резкого изображения визирной нити. Направьте зрительную трубу на удаленный предмет и передвигайте внутренний тубус зрительной трубы (не смещая окуляра относительно визирной нити) до тех пор, пока изображение предмета и визирной нити будут видны отчетливо, т.е. пока они не будут в фокальной плоскости объектива зрительной трубы.
Включите ртутную лампу и осветите ею щель коллиматора. Повернув зрительную трубу в направлении выходящего из коллиматора пучка, не сбивая окуляра, совместите визирную нить с изображением щели.
Передвигая внутренний тубус коллиматора, установите его так, чтобы изображение щели стало резким и отсутствовало параллактическое смещение изображений визирной нити и щели.
Лабораторная работа. ИССЛЕДОВАНИЕ СПЕКТРА ИСПУСКАНИЯ ВОДОРОДА И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА
Цель работы: исследование серии Бальмера в видимой области спектра атомарного водорода и определение постоянной Ридберга.
Теоретические сведения
Изолированные газы в виде разряженного газа или паров металла испускают спектр, состоящий из отдельных спектральных линий разной интенсивности, соответствующих различным длинам волн. В соответствии с этим спектр испускания атомов называется линейчатым.
Швейцарский ученый И.Бальмер в результате длительного изучения линейчатого спектра атомарного водорода установил закономерности в расположении линий в видимой области спектра. В настоящее время в спектре водорода наблюдается 6 серий, которые описываются формулой
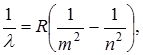 (11.1)
(11.1)
где λ – длина волны соответствующей линии, R=1,097.107 м-1 – постоянная Ридберга, m и n – целые числа, причем n принимает значения, начиная с m+1.
m определяет спектральную серию: m=1 – серия Лаймана, m=2 – серия Бальмера, m=3 – серия Пашена, m=4 – серия Брекетта, m=5 – серия Пфунда, m=6 – серия Хемфри.
Изучение атомных спектров послужило ключом к познанию строения атома. Задача объяснения закономерности в линейчатых спектрах излучения привела к проблеме строения атома. Попытки построить модель атома, которая смогла бы объяснить возникновение спектров испускания, были предприняты Томсоном (1903 г.), Резерфордом (1913 г.) и потерпели неудачу.
Первая попытка построения неклассической теории атома была предпринята Н.Бором в 1913 г. В основе этой теории лежала идея связать в единое целое эмпирические закономерности линейчатых спектров (формулу Бальмера), ядерную модель Резерфорда и квантовый характер излучения света (теория Планка). В теории Бора не содержалось принципиального отказа от описания поведения электрона в атоме при помощи законов классической физики. Однако Бору пришлось дополнить классическое описание состояния электрона в атоме некоторыми ограничениями. Эти ограничения были сформулированы в виде постулатов.
Первый постулат Бора (постулат стационарных состояний) заключается в следующем: из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются только некоторые дискретные орбиты, удовлетворяющие определенным квантовым состояниям, энергии которых составляют дискретный ряд: W1 ,W2,W3,...В стационарном состоянии атом не излучает.
Второй постулат Бора (правила квантования орбит): в стационарном состоянии атома электрон движется только по таким орбитам, для которых момент импульса электрона удовлетворяет условию:
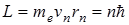 , (11.2)
, (11.2)
где ħ – постоянная Планка, равная 1,054.10-34 Дж.с; n=1,2,3,…; me – масса электрона; rn – радиус соответствующей орбиты.; vn – скорость электрона.
Третий постулат Бора (правило частот): при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии.
Излучение происходит при переходе из состояния с большей энергией в состояние с меньшей энергией, т.е. при переходе электрона с орбиты, более удаленной от ядра, на более ближнюю к ядру:
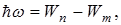 (11.3)
(11.3)
где 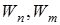 – энергия электрона на соответствующей орбите;
– энергия электрона на соответствующей орбите; 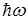 – квант энергии;
– квант энергии; 
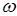 – циклическая частота излучения.
– циклическая частота излучения.
Теория Бора дала возможность построить модель атома водорода и водородоподобных ионов 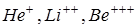 . Согласно этой теории атом состоит из ядра и электрона, движущегося по круговым стационарным орбитам. Электрон удерживается на круговой орбите кулоновской силой. Определим полную энергию электрона в водородоподобном атоме. Полная энергия электрона на орбите складывается из кинетической энергии электрона
. Согласно этой теории атом состоит из ядра и электрона, движущегося по круговым стационарным орбитам. Электрон удерживается на круговой орбите кулоновской силой. Определим полную энергию электрона в водородоподобном атоме. Полная энергия электрона на орбите складывается из кинетической энергии электрона  и потенциальной энергии взаимодействия электрона с ядром
и потенциальной энергии взаимодействия электрона с ядром 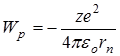 , где:
, где:
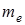 – масса электрона;
– масса электрона;
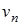 – линейная скорость электрона на орбите;
– линейная скорость электрона на орбите;
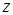 – зарядовое число ядра атома;
– зарядовое число ядра атома;
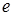 – заряд электрона;
– заряд электрона;
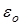 – электрическая постоянная;
– электрическая постоянная;
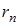 – радиус орбиты.
– радиус орбиты.
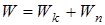 . (11.4)
. (11.4)
Кулоновская сила сообщает электрону центростремительное ускорение, т.е.
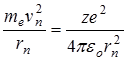 (11.5)
(11.5)
Из (11.5) следует, что
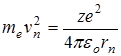 , (11.6)
, (11.6)
т.е. потенциальная энергия равна удвоенному значению его кинетической энергии:
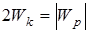 . (11.7)
. (11.7)
Подставив (11.5) в (11.4), получим:
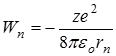 . (11.8)
. (11.8)
Для определения радиуса орбиты 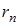 воспользуемся вторым постулатом Бора
воспользуемся вторым постулатом Бора 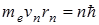 и равенством (11.5). Решив систему двух уравнений относительно
и равенством (11.5). Решив систему двух уравнений относительно 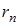 , получим:
, получим:
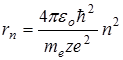 . (11.9)
. (11.9)
Таким образом rn ~n2, т.е. с ростом номера орбиты радиус ее растет. Для водорода (z=1) при n=1: 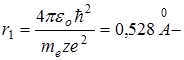 радиус первой Боровской орбиты.
радиус первой Боровской орбиты.
Подставив (11.9) в выражение (11.8), получим:
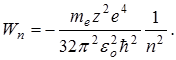 (11.10)
(11.10)
Таким образом, из выражения (11.10) следует:
1. Полная энергия электрона в атоме отрицательна.
2. Энергия электрона в атоме принимает дискретный ряд значений, которые можно представить на рисунке 11.1
Рисунок 11.1. Энергетический спектр атома
При n=1 энергия минимальна, при n→∞ энергия электрона максимальна, и он покидает атом. Атом при этом ионизируется.
Воспользуемся третьим постулатом Бора и формулой энергии электрона (11.10), определим длину волны излучения при переходе электрона из одного энергетического состояния в другое.
Длина волны связана с циклической частотой соотношением 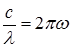 , где с – скорость света в вакууме. Поскольку
, где с – скорость света в вакууме. Поскольку 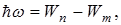 то
то 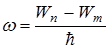 , где
, где 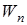 – энергия на n уровне;
– энергия на n уровне;
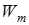 – энергия на m уровне. Причем n>m.
– энергия на m уровне. Причем n>m.
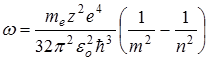 . (11.11)
. (11.11)
Для длины волны формулу (11.11) можно записать в виде:
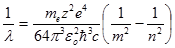 . (11.12)
. (11.12)
Обозначив 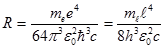 получим обобщенную формулу Бальмера:
получим обобщенную формулу Бальмера:
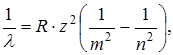 (11.13)
(11.13)
где R – постоянная Ридберга.
Теория Бора смогла объяснить факт испускания света атомом: при переходе электрона из состояния с большей энергией Wn в состояние с меньшей энергией Wm атом излучает квант энергии 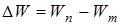 .(На рисунке 11.2 – переходы 2 и 3).
.(На рисунке 11.2 – переходы 2 и 3).
При поглощении порции энергии ΔW электрон переходит из основного состояния (n=1) в возбужденное (переход 1 на рисунке 11.2). В этом состоянии атом пребывает незначительный промежуток времени Δt~10-8 с, а затем переходит в основное состояние, причем этот переход может осуществляться ступенчато.
Рисунок 11.2. Возможные переходы электронов в атоме
Описание установки
Для исследования спектра испускания водорода применяется гониометр типа Федорова. Этот гониометр представляет собой двухтрубный спектроскоп, принципиальная схема которого приведена на рисунке 11.3.
Рисунок 11.3. Принципиальная схема гониометра:
S – источник света; 1 – коллиматор; 2 – призма трехгранная; 3 – зрительная труба.
Коллиматор – это труба со щелью на одном конце, ширину которой можно менять регулировочным винтом. На другом конце коллиматора расположена ахроматическая собирающая линза. Коллиматор создает параллельный пучок лучей, падающих на призму. Зрительная труба имеет объектив и окуляр, при помощи которого рассматривается спектр исследуемого вещества. Призма обладает относительно большой дисперсией, поэтому весь спектр одновременно в поле зрения не виден. Для определения длин волн, излучаемых исследуемым веществом, необходимо знать дисперсионную кривую прибора, т.е. графическую зависимость углового расположения спектральных линий в поле зрения окуляра от длины волны. Строится дисперсионная кривая при помощи линейчатых спектров элементов, длины волн которых известны (например, ртуть, гелий). По дисперсионной кривой можно определить длины волн всех спектральных линий водорода.
11.3 Приборы и материалы: монохроматор, ртутная лампа, водородная трубка.
Порядок выполнения работы
1.Градуировка шкалы спектрометра.
1.1. Расположить гониометр перед окном ртутной лампы.
1.2. Включить вентилятор.
1.3. Включить ртутную лампу.
1.4. Добиться наибольшей четкости линий спектра ртути, уменьшая размер входной щели коллиматора.
1.5. Записать деления шкалы гониометра α, соответствующие наиболее ярким линиям спектра ртути. (таблица 11.1)
1.6. На миллиметровой бумаге построить градуировочную кривую прибора 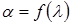 по табличным данным.
по табличным данным.
Таблица 11.1
2. Определение длин волн серии Бальмера и постоянной Ридберга.
2.1. Переставить гониометр к водородной трубке.
2.2. Включить водородную трубку.
2.3. Не изменяя положения зрительной трубы и коллиматора относительно призмы, добиться наблюдения линий серии Бальмера.
2.4. Записать показания шкалы гониометра, соответствующие видимым линиям спектра водорода. (табл.11.2)
Таблица 11.2
| Линия
| Красная
| Зелено-голубая
| Синяя
| Фиолетовая
|
| n
| 3
| 4
| 5
| 6
|
| α, град
|
|
|
|
|
| λ, нм
|
|
|
|
|
| R, м-1
|
|
|
|
|
2.5. Определить длины волн спектральных линий водорода, пользуясь градуировочной кривой.
2.6. Произвести расчет постоянной Ридберга, используя формулу:
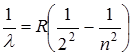
2.7. Найти среднее значение постоянной Ридберга.
2.8. Сравнить полученное значение с теоретическим.
2.9. Оценить погрешность результата.
Контрольные вопросы
1. Опишите модель атома по Резерфорду-Бору.
2. Сформулируйте постулаты Бора.
3. Выведите формулу для расчета энергии атома водорода.
4. Получите сериальную формулу Бальмера.
5. Каков физический смысл и числовое значение постоянной Ридберга?
6. Опишите процессы излучения и поглощения атома.
Техника безопасности
1. Без разрешения преподавателя или лаборанта установку не включать.
2. Избегать прямого попадания излучения ртутной лампы в глаза.
3. По окончании работы отключить установку от сети.





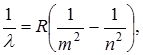 (11.1)
(11.1)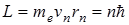 , (11.2)
, (11.2)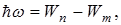 (11.3)
(11.3)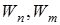 – энергия электрона на соответствующей орбите;
– энергия электрона на соответствующей орбите; 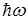 – квант энергии;
– квант энергии; 
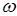 – циклическая частота излучения.
– циклическая частота излучения.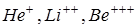 . Согласно этой теории атом состоит из ядра и электрона, движущегося по круговым стационарным орбитам. Электрон удерживается на круговой орбите кулоновской силой. Определим полную энергию электрона в водородоподобном атоме. Полная энергия электрона на орбите складывается из кинетической энергии электрона
. Согласно этой теории атом состоит из ядра и электрона, движущегося по круговым стационарным орбитам. Электрон удерживается на круговой орбите кулоновской силой. Определим полную энергию электрона в водородоподобном атоме. Полная энергия электрона на орбите складывается из кинетической энергии электрона  и потенциальной энергии взаимодействия электрона с ядром
и потенциальной энергии взаимодействия электрона с ядром 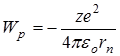 , где:
, где: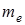 – масса электрона;
– масса электрона;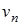 – линейная скорость электрона на орбите;
– линейная скорость электрона на орбите;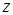 – зарядовое число ядра атома;
– зарядовое число ядра атома;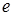 – заряд электрона;
– заряд электрона;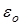 – электрическая постоянная;
– электрическая постоянная;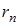 – радиус орбиты.
– радиус орбиты.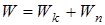 . (11.4)
. (11.4)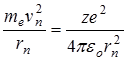 (11.5)
(11.5)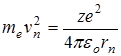 , (11.6)
, (11.6)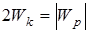 . (11.7)
. (11.7)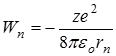 . (11.8)
. (11.8)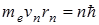 и равенством (11.5). Решив систему двух уравнений относительно
и равенством (11.5). Решив систему двух уравнений относительно 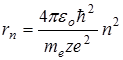 . (11.9)
. (11.9)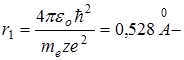 радиус первой Боровской орбиты.
радиус первой Боровской орбиты.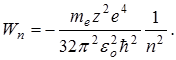 (11.10)
(11.10)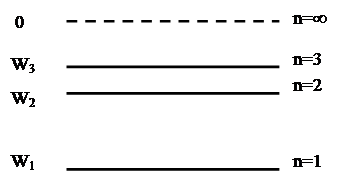
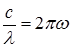 , где с – скорость света в вакууме. Поскольку
, где с – скорость света в вакууме. Поскольку 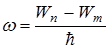 , где
, где 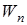 – энергия на n уровне;
– энергия на n уровне;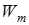 – энергия на m уровне. Причем n>m.
– энергия на m уровне. Причем n>m.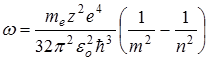 . (11.11)
. (11.11)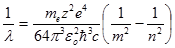 . (11.12)
. (11.12)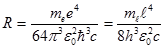 получим обобщенную формулу Бальмера:
получим обобщенную формулу Бальмера: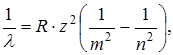 (11.13)
(11.13)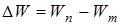 .(На рисунке 11.2 – переходы 2 и 3).
.(На рисунке 11.2 – переходы 2 и 3).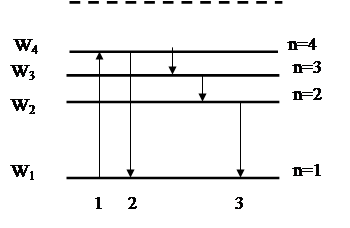

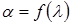 по табличным данным.
по табличным данным.