Скорость. Вычисление пройденного пути. Ускорение

§ 1. Скорость

 

 

Слово «скорость» мы часто используем в своей речи и на обыде нном

уровне представляем себе, что оно означает величину, характеризующую либо

быстроту движения, либо быстроту какого -либо процесса.

Однако, для того, чтобы ввести в механику точный физический термин

«скорость», потребовалось создать новую область математ                       ики – научиться оп                                                                     е-

рировать с бесконечно малыми величинами. Известны многочисленные пар а-

доксы, связанные с проблемой скорости движения. Вот один из них, принадл е-

жащий древнегреческому философу Зенону Элейскому, жившему примерно

2  500 лет тому назад. В этом парадоксе утверждается, что быстроногий Ахил-

лес никогда не сможет догнать медлительную черепаху. Вот как излагает ра с-

суждения Зенона известный американский физик Ричард Фейнман в первом

томе своих лекций по физике. Предположим, что Ахиллес бегает в десять раз

быс т рее черепахи. Пусть в начале состязания черепаха находилась в 100 метрах

вп е реди Ахиллеса. Тогда ко времени, когда Ахиллес пробежит эти 100 метров,

черепаха окажется в 10 метрах впереди него. Пробежав и эти 10 метров, Ахи л-

лес увидит черепаху в 1 м етре впереди себя. За то время, пока он пробежит этот

метр, черепаха пройдет 10 сантиметров и так далее… до бесконечности. След о-

вательно, в любой момент времени черепаха будет впереди Ахиллеса, и он н и-

когда не сможет перегнать ее! В чем ошибочность этих ра ссуждений? Коне ч-

ный интервал времени можно разделить на бесконечное число частей. Но бе с-

конечное число этапов до того места, где Ахиллес поравняется с черепахой,

вовсе не о значает                                                 бесконечное количество времени. Для того, чтобы научиться

правильно опериро                                                                                         вать с бесконечно малыми величинами, человечеству пон                                     а-

добилось примерно 2                                                                                     000 лет. Честь создания дифференциального и интеграл                                           ь-

ного и счисления принадлежит И. Ньютону (наряду с Г. Лейбницем). В своем

гранд                                                                                        иозном труде «Математические начала натуральной фило                         софии» (1687 г.)

Ньютон сформулировал исходные понятия и основные законы классической

мех а ники.

Сейчас мы дадим точное и строгое определение физического термина

«скорость». Исходя из этого определения, выясним свойства скорости.

Скорость –                    это производная радиус -вектора по времени.

 

 

 

либо, применяя другое

обозначение производной             .          (2.1)

по времени,

 

 

 

 

17

Как видно из этого определения, скорость – величина векторная, т.е. когда

употребляют термин «скорость», имеют в виду вектор, который имеет две х а-

рак теристики: направление и модуль.

Скорость направлена по касательной к траектории.                      Это можно устан                                                                             о-

вить, проанализировав определение скорости (2.1).

Так как

,                                          (2.1а)

 

 

 

LLLLLLLLLL. направление вектора  совпадает с предельным направлением вектора . На рис. 2.1а, 2.1б, 2.1в показаны этапы предельного перехода для плоского

движения, когда материальная точка движется по произвольной траект ории. 

На рис. 2.1а изображ             ены радиус                                         -векторы материальной точки для моме н-

тов времени t1 и                                                              t2, а также вектор перемещения этой материальной

точки за промежуток времени                    Отношение перемещения      к

промежутку времени t дает среднюю скорость < v> материальной точки за

пром                        ежуток времени t:

 

 

 

(2.1б)

 

 

Направление средней скорости, как следует из ее определения (2.1б), со в-

падает с направлением вектора переме           щения .

 

 

При уменьшении промежутка времени t радиус          -вектор  приближается к

.  При этом вектор перемещения   меняет свое направление, он поворач и-

вается против часовой                                             стрелки. Модуль вектора  уменьшается. Это пром                                           е-

жуточное положение при совершении предельного перехода ( t 0) зафикс и-

ровано на рис. 2.1б.

 

 

При дальнейшем уменьшении t и приближении  к направление ве к-

тора  приближается к направлению касательной к траектории. Как известно

из геометрии, касательная есть предельное положение секущей.

Значит, когда предельный переход будет завершен, бесконечно малый вектор

перемещен     ия  будет направлен по касательной к траектории.

Следовательно, и вектор скорости будет направлен по касательной к

траектории . Это изображено на рис. 2.1в.

 

 

 

 

 

 

 

18

Рис. 2.1а

 

 

 

 

 

 

 

 

 

r   

2

r 

 

 

 

 

 

 

x

 

 

 

 

Рис. 2.1б

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 2.1в

 

 

 

 

19

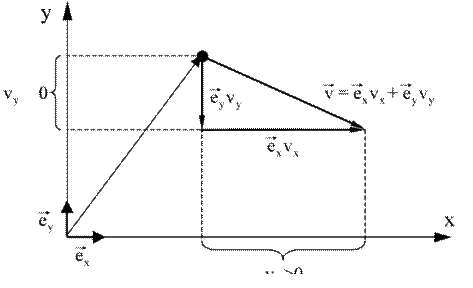
Компоненты скорости

На рис. 2.2 изображен вектор скорости  материальной точки, движуще й-

ся по плоскости                    x, y. Вектор                                                    можно разложить на два составляющих его ве                                                        к-

тора                      .

 

 

 

 

 

 

 

Vу 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 2.2

Компоненты скорости, т.е. проекции вектора  на координатные оси об о-

значены                                                              vx, vy. Так как на рис. 2.2 вектор направлен по оси х, то комп                                               о-

нента скорости v                            у нас направлен против оси, значит, соо т-

x > 0. Вектор

ветствующая комп                      онента скорости vy < 0.

Из определения (2.1) и формулы (1.1) следует, что для трехмерного пр о-

странства скорость в декартовых координатах                                          выражается следующим обр  а-

зом: 

(2.1а)

С  другой стороны:

,                                (2.1б)

откуда

(2.2)

 

 

т.е. компоненты скорости в декартовых координатах равны производным с о-

ответствующих коор                       динат по времени .

Модуль скорости                                                      – это производная пути по времени             . В самом деле, при

(см. рис. 1.8, 2.1а, 2.1б). Используя это, получим для модуля

скорости из определения (2.1а):

 

 

 

 

 

20

.                   (2.3)

 

 

 

Выра зим модуль скорости через ее компоненты. По теореме Пифагора (см.

рис. 2.2):

.

 

 

 

В  трехмерном пространстве                                    и модуль скорости: (2.4)

 

 

 

 

. 2. Вычисление пройденного пути

Для равномерного движения , т.е. для движения с постоянной по модулю

скоростью:                     , путь равен:

,                                                   (2.5)

где s12 – весь путь (рис. 2.3);

t – весь отрезок времени;

–  const.

 

 

 

 

 

 

 

 

Рис. 2.3

Формула (2.5), известная по школьному курсу физики, следует из формулы

(2.3). Запишем формулу (2.3) в следующем виде:

 

 

,

тогда

,                                                  (2.3а)

здесь ds – бесконечно малый отрезок пути, пройденный за бесконечно малое

время dt. 

Складывая все                     ds, получим                                   , сумма всех dt даст время движения           t. Оп е-

рация сложения бесконечно м алых величин носит в математике название и н-

тегрир ования. Интегрируя (2.3а), получим:

 

 

 

 

21

.

 

 

В  правой части мы вынесли за знак интеграла скорость v, так как она в на-

шем случае постоянна. Интеграл от        ds есть            s12, а интеграл от dt – время д виж е-

ния t, следовательно, мы получим формулу, совпадающую с (2.5):

 

 

 

 

 

Для произвольного движения (рис. 2.4), т.е. для движения с переменной

 

скоростью разобьем весь путь на очень маленькие участки s:

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 2.4

 

 

Значения модуля скорости  в течение отрезка времени     приблиз и-

тельно постоянны, если  достаточно малы.

В  пределе:

 

 

 

 

,                             (2.6)

 

 

 

т.е. п уть – это определенный интеграл от   модуля скорости по времени.

Так как модуль скорости                                                                        – величина положительная, то путь всегда пол                                                       о-

жителен и может только возрастать с течением времени.

 

 

 

§ 3. Ускорение

В  общем случае скорость материальной точки может изме няться как по

величине (т.е. по модулю), так и по н аправлению. Быстроту этого изменения

характеризует векторная величина, которую называют термином «ускор ение».

Ускорение – это производная скорости по времени.

 

 

 

 

 

22

 или              .                       (2.7)

 

 

 

 

Учитывая, что         (2.1), получим:

 

 

 

 

.                                  (2.8)

 

 

 

Ускорение –                                    вторая производная радиус -вектора по времени . Произво                            д-

ную по времени от какой -либ о величины называют скоростью изменения этой

вел и чины.            Ускорение – это скорость изменения скорости.

Вектор            ускорения                                    , так же, как и векторы , можно разложить на

составляющие:

,

где а               х, аy, а z – компоненты ускорения.

Из определения (2.7) и формулы (2.1б) следует, что:

 

 

 

,                    (2.9)

 

 

т.е. компоненты ускорения равны производным по времени от соответству ю-

щих компонент скорости.

Используя формулы (2.8) и (1.1 ), получим, что:

 

 

 

,                      (2.9а)

 

 

т.е. компоненты ускорения равны вторым производным по времени от соо т-

ветствующих координат материальной точки.

 

 

 

§ 4. Нахождение зависимости скорости от времени

Запишем первую из формул ( 2.7) в следующем виде:

.                                           (2.7а)

Формула (2.7а) позволяет найти приращение скорости  за бесконечно

малый промежуток времени   dt. Если известна начальная скорость

 

 

 

 

 

23

,   то, используя (2.7а), можно найти скорость спустя бесконечно

малый интервал dt:

(2.10)

 

 

Если нам известна зависимость ускорения от времени, т.е. функция

LLLLLLLLLL. н ачатый формулой (2.10) процесс вычисления зависимости                                          - скорости

от времени – можно бесконечно продолжать. В математике эта операция наз ы-

вается интегрированием. Возьмем определенный интеграл в пределах от нуля

до t от обеих частей р авенства (2.7а):

 

 

 

 

(2.11)

 

 

 

Как известно из математики, интеграл от дифференциала  равен разн о-

сти значений функции  на верхнем и нижнем предела                            х. Тогда из (2.11) пол                   у-

чим:

 

 

 

 

 

 

откуда для     имеем:

 

 

 

(2.12)

Для нахождения зависимости   по формуле (2.12) необходимо в ка ждом

конк ретном случае взять интеграл от ускорения по времени.

 

 

 

 

 

ИТОГИ ЛЕКЦИИ № 2

1.  Скорость – производная радиус -вектора по времени (2.1):

 

 

 

 

 

 

Напра                    влена скорость  по касательной к траектории.

2.                                                                                  Компоненты скорости  равны производным соответ                                                  ствующих коорд и-

нат по времени (2.2):

 

 

 

 

 

 

 

 

24

3.   Модуль скорости – производная пути s по времени (2.3):

 

 

 

 

 

 

4.  Модуль скорости связан с ее компонентами следующим образом (2.4):

 

 

 

 

 

 

5.                                          При равномерном движении , т.е. при пройденный путь

связан с временем движения t простой формулой (2.5):

 

 

 

 

 

6.   Для произвольного движения путь равен определенному интегралу от 

модуля скорости по времени ( 2.6)

 

 

 

 

 

 

7.  Ускорение – это производная скорости по времени (2.7):

 

 

 

 

 

 

8.  Ускорение – это вторая производная радиус-вектора по времени (2.8):

 

 

 

.

 

 

 

9.  Компоненты ускорения ах, аy, а z равны производ ным по времени от с                  о-

ответствующих компонент скорости (2.9):

 

 

 

 

 

 

и  вторым производным по времени от соответствующих координат (2.9а):

 

 

 

.

 

 

10.   Зависимость скорости материальной точки от времени может быть

найд       ена (2.1 1), если известно ускорение как функция времени:

 

 

 

.

 

 

 

25

 ЛЕКЦИЯ № 3