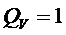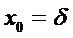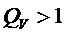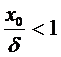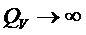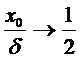; … ;
 так как
так как 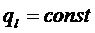
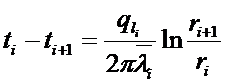
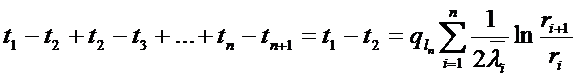

 полное линейное термическое сопротивление многослойной
полное линейное термическое сопротивление многослойной
цилиндрической стенки.
Температурное поле:
Уравнение теплопроводности после первого интегрирования:
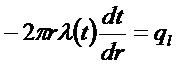
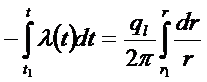
Пусть 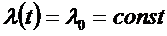 (не зависит от температуры)
(не зависит от температуры)
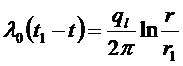
Подставляя в это выражение значение для ql, получим:
температурное поле в однослойной стенке.

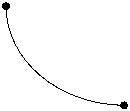
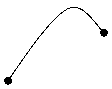
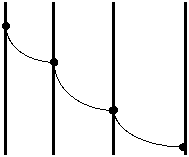
 Так как плотность теплового потока уменьшается с увеличением радиуса, то кривая имеет следующий вид:
Так как плотность теплового потока уменьшается с увеличением радиуса, то кривая имеет следующий вид:
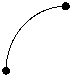 t1 t2
t1 t2
t2
t3
t1
t4
 Обоснование подобного вида кривой следует из понятия производной и касательной к графику функции. Из математики известно, что тангенс угла наклона касательной к графику функции в некоторой точке есть значение производной этой функции в данной точке. Из теории тепломассообмена
Обоснование подобного вида кривой следует из понятия производной и касательной к графику функции. Из математики известно, что тангенс угла наклона касательной к графику функции в некоторой точке есть значение производной этой функции в данной точке. Из теории тепломассообмена
известно, что: .
t Если провести к этому графику множество касательных, то при увеличении координаты r угол j уменьшается.
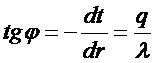
 t1
t1
(*)
t 2 Как было сказано выше, поток тепла q
r с увеличением радиуса r уменьшается.

 j Если значение l не изменяется, то из
j Если значение l не изменяется, то из
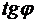 выражения (*) следует что значение
выражения (*) следует что значение
так же уменьшается.
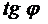 Из графика видим, что уменьшение значения j а значит и при увеличении r возможно только при данном поведении кривой (кривая вогнутая а не выпуклая).
Из графика видим, что уменьшение значения j а значит и при увеличении r возможно только при данном поведении кривой (кривая вогнутая а не выпуклая).
Какое температурное поле в i - том слое?
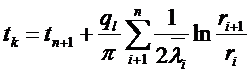
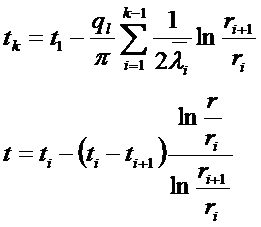 Определим граничные значения температур:
Определим граничные значения температур:
Температурное поле и плотность теплового потока в шаровой (сферической) стенке.
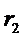




 Заданы:
Заданы:
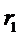 Так же заданы граничные условия первого рода:
Так же заданы граничные условия первого рода:
Здесь не существует торцевого эффекта, задача является одномерной:
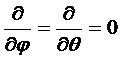
Уравнение теплопроводности для нашего случая:
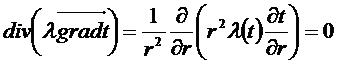
Проинтегрируем:
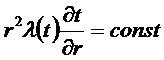
Рассмотрим два геометрических тела:
1) Шар – может выделять тепло, если есть внутренние источники тепла:
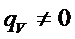

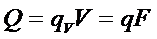
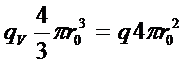
2) Шаровая (сферическая стенка)
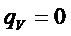


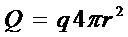 - текущий радиус
- текущий радиус
Домножим на 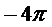 :
:
 (*)
(*)
В сферической стенке, полня передаваемая (переносимая) энергия не зависит от радиуса и является величиной постоянной.
Умножим выражение (*) на 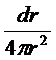 и проинтегрируем:
и проинтегрируем:
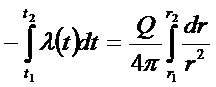 ; умножим на
; умножим на 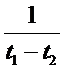
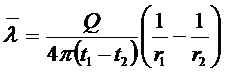


(*)
термическое сопротивление
шарового слоя.
Для многослойной сферической стенки:
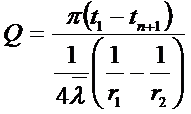
Температурное поле:
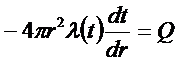
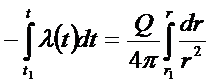
Рассмотрим простейший вариант: пусть 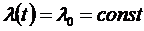
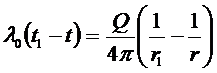

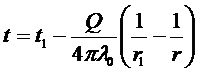 ; подставим значение для Q из выражения (*):
; подставим значение для Q из выражения (*):
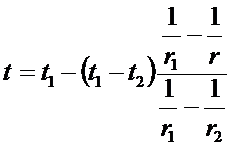
Это температурное поле для шарового слоя (гиперболическая функция).
Решение задач теплопроводности для граничных условий третьего рода.
Плоская стенка. Теплопередача.



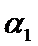
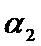
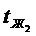
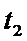
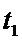
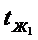
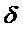

Заданы: 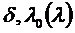
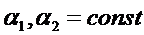 Значение коэффициентов теплоотдачи
Значение коэффициентов теплоотдачи
Среда представляется текучей
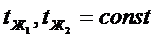 Кроме этого известно значение температур жидкости:
Кроме этого известно значение температур жидкости:
Вследствие того, что 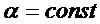 и
и 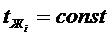 , отсюда
, отсюда 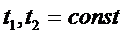
Граничные условия третьего рода заключаются в том, что нам известна плотность теплового потока:
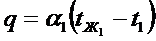 - граничные условия левой части стенки.
- граничные условия левой части стенки.
Рассмотрим связь между плотностью теплового потока и температурой стенки:
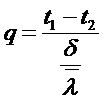
(см. решение ранее)
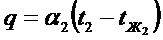 - граничные условия для правой стенки.
- граничные условия для правой стенки.
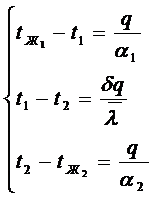 Переписывая наши выражения, получим:
Переписывая наши выражения, получим:
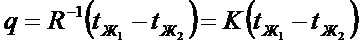 Сложив, получим:
Сложив, получим:
Мы получили выражения для плотности теплового потока при теплопередаче
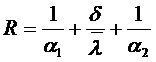 - термическое сопротивление теплопередаче через плоскую стенку.
- термическое сопротивление теплопередаче через плоскую стенку.

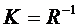 - коэффициент теплопередачи через плоскую стенку
- коэффициент теплопередачи через плоскую стенку 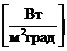
- термическое сопротивление материала плоской стенки.
- термические сопротивления теплоотдаче.
Многослойная плоская стенка. Теплопередача.
Записывая выражение для разности температур между слоями и по гипотезе Ньютона -Рихмана, мы получим следующий результат:
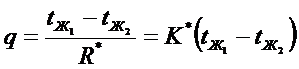
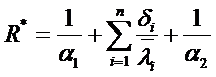 - термическое сопротивление теплопередаче через многослойную плоскую стенку.
- термическое сопротивление теплопередаче через многослойную плоскую стенку.
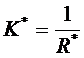 - коэффициент теплопередачи через многослойную плоскую стенку.
- коэффициент теплопередачи через многослойную плоскую стенку.
Цилиндрическая стенка. Теплопередача.







Заданы:
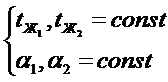
Нам известно, что:
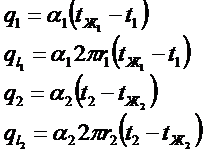
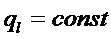
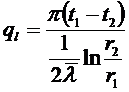 (см. решение ранее)
(см. решение ранее)
Переписывая наши выражения для разности температур и сложив их, получим:
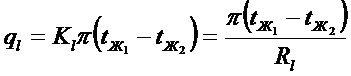
где: 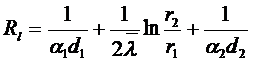 - термическое сопротивление теплопередачи через цилиндрическую стенку
- термическое сопротивление теплопередачи через цилиндрическую стенку 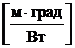
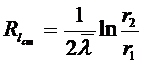 - термическое сопротивление теплопроводности стенки.
- термическое сопротивление теплопроводности стенки.

- линейное термическое сопротивление теплоотдаче через цилиндрическую стенку
Многослойная цилиндрическая стенка. Теплопередача.
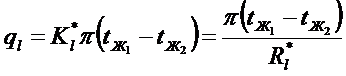
где: 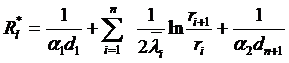 - линейное термическое сопротивление теплопередаче для многослойной цилиндрической стенки.
- линейное термическое сопротивление теплопередаче для многослойной цилиндрической стенки.
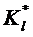 - линейный коэффициент теплопередачи через многослойную цилиндрическую стенку.
- линейный коэффициент теплопередачи через многослойную цилиндрическую стенку.
Запишем связь между плотностями теплового потока, учитывая что в цилиндрической стенке:
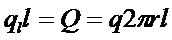
где 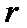 - любой текущий радиус:
- любой текущий радиус: 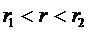
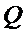 - передаваемое через поверхность тепло.
- передаваемое через поверхность тепло.
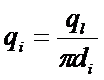 В нашем случае:
В нашем случае:
Плотность теплового потока на единицу поверхности с ростом радиуса уменьшается.
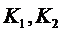 - коэффициенты теплопередачи, отнесённые к поверхности 1 или 2.
- коэффициенты теплопередачи, отнесённые к поверхности 1 или 2.
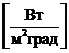
Существует понятие тонких цилиндрических стенок.
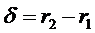 Возьмём
Возьмём 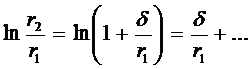 где
где
Если 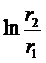 можно с достаточной точностью представить как первый член разложения, то это тонкая стенка.
можно с достаточной точностью представить как первый член разложения, то это тонкая стенка.
Для тонких стенок выражение для полного количества тепла. передаваемого через цилиндрическую стенку может быть записано в следующем виде.
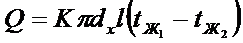 (*)
(*)
Причём К рассчитывается как для плоской стенки а диаметр dx берётся по стороне с наименьшим коэффициентом теплоотдачи. Если коэффициенты теплоотдачи близки друг другу то расчётный диаметр является средним арифметическим:

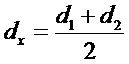
Докажем это:
Учитывая, что для тонкой цилиндрической стенки 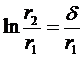 , запишем:
, запишем:
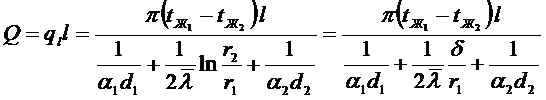
Если стенка тонкая, то мы можем предположить, что 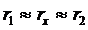 , то есть:
, то есть:
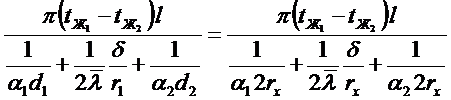

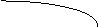
Преобразуем знаменатель, вынося за скобки 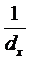 :
:
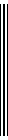
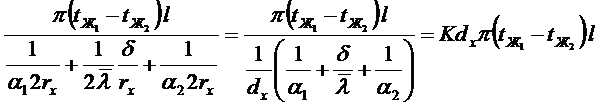
Справедливость выражения (*) для цилиндрической тонкой стенки доказана.
Температурное поле в пластине (бесконечной плоской стенке) с внутренними источниками тепла.



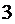

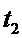
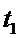







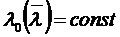
 Будем считать, что
Будем считать, что 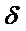 - известно,
- известно,

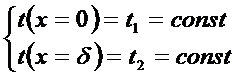
 - изотропные источники (равномерно распределённый по стенке),
- изотропные источники (равномерно распределённый по стенке),  = const, не зависит от координаты.
= const, не зависит от координаты.
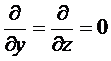
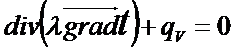
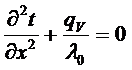 ;
; 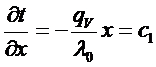 ;
;
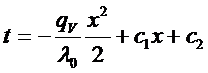
Воспользуемся граничными условиями:
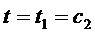


x=0
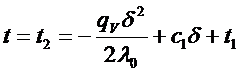
 x = d:
x = d:
x=d
Отсюда:
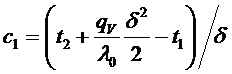
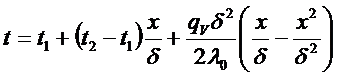
Будем предполагать, что экстремум функции существует в точке 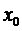
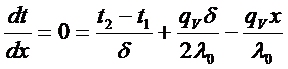

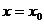
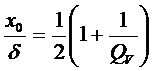

1. 
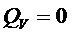
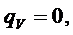
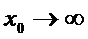 (экстремума нет)
(экстремума нет)
2. 
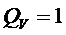
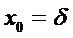
3. 
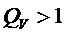
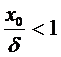
4. 
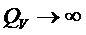
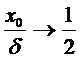
Если пластину делим серединной плоскостью, то существование экстремума в левой полуплоскости невозможно!!!



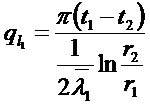
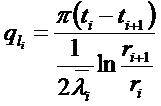
 так как
так как 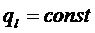
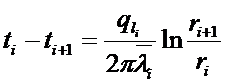
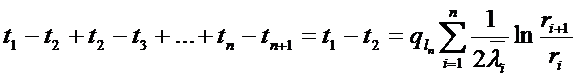
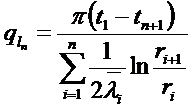

 полное линейное термическое сопротивление многослойной
полное линейное термическое сопротивление многослойной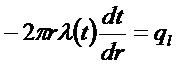
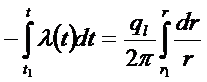
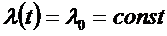 (не зависит от температуры)
(не зависит от температуры)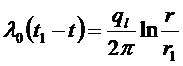
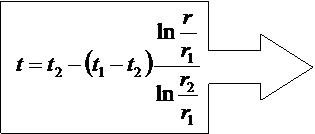


 t1 t2
t1 t2 Обоснование подобного вида кривой следует из понятия производной и касательной к графику функции. Из математики известно, что тангенс угла наклона касательной к графику функции в некоторой точке есть значение производной этой функции в данной точке. Из теории тепломассообмена
Обоснование подобного вида кривой следует из понятия производной и касательной к графику функции. Из математики известно, что тангенс угла наклона касательной к графику функции в некоторой точке есть значение производной этой функции в данной точке. Из теории тепломассообмена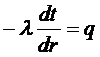


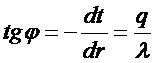

 t1
t1 
 j Если значение l не изменяется, то из
j Если значение l не изменяется, то из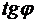 выражения (*) следует что значение
выражения (*) следует что значение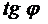 Из графика видим, что уменьшение значения j а значит и при увеличении r возможно только при данном поведении кривой (кривая вогнутая а не выпуклая).
Из графика видим, что уменьшение значения j а значит и при увеличении r возможно только при данном поведении кривой (кривая вогнутая а не выпуклая).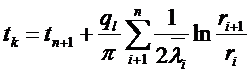
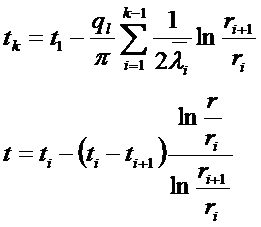 Определим граничные значения температур:
Определим граничные значения температур: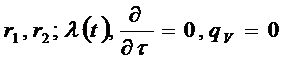
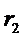




 Заданы:
Заданы: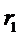 Так же заданы граничные условия первого рода:
Так же заданы граничные условия первого рода: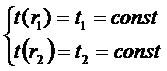
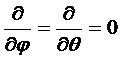
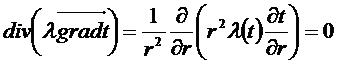
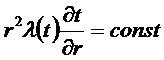
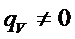

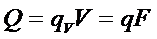
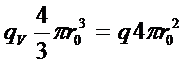
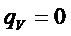


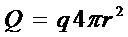 - текущий радиус
- текущий радиус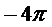 :
: (*)
(*)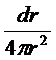 и проинтегрируем:
и проинтегрируем: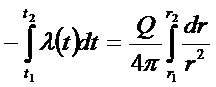 ; умножим на
; умножим на 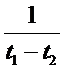
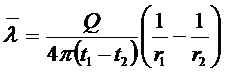


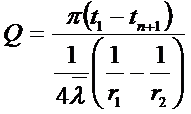
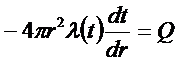
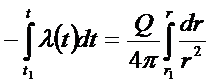
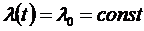
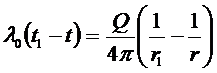

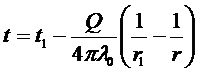 ; подставим значение для Q из выражения (*):
; подставим значение для Q из выражения (*):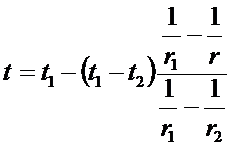



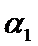
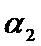
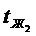
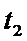
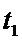
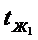

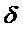

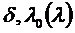
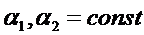 Значение коэффициентов теплоотдачи
Значение коэффициентов теплоотдачи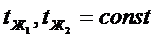 Кроме этого известно значение температур жидкости:
Кроме этого известно значение температур жидкости: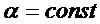 и
и 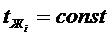 , отсюда
, отсюда 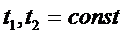
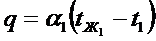 - граничные условия левой части стенки.
- граничные условия левой части стенки. 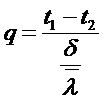
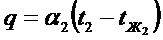 - граничные условия для правой стенки.
- граничные условия для правой стенки.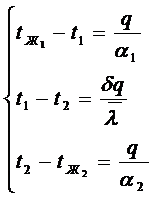 Переписывая наши выражения, получим:
Переписывая наши выражения, получим: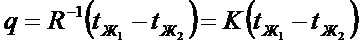 Сложив, получим:
Сложив, получим: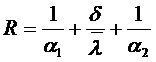 - термическое сопротивление теплопередаче через плоскую стенку.
- термическое сопротивление теплопередаче через плоскую стенку. 
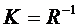 - коэффициент теплопередачи через плоскую стенку
- коэффициент теплопередачи через плоскую стенку 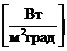
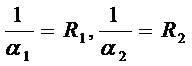
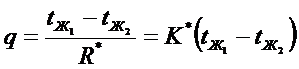
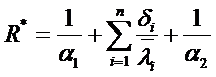 - термическое сопротивление теплопередаче через многослойную плоскую стенку.
- термическое сопротивление теплопередаче через многослойную плоскую стенку.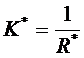 - коэффициент теплопередачи через многослойную плоскую стенку.
- коэффициент теплопередачи через многослойную плоскую стенку.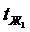
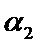
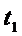
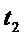
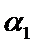





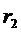



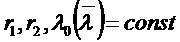
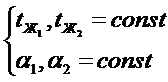
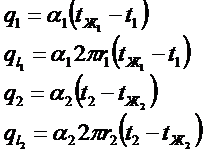
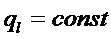
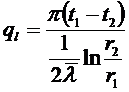 (см. решение ранее)
(см. решение ранее)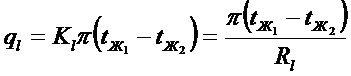
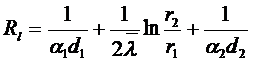 - термическое сопротивление теплопередачи через цилиндрическую стенку
- термическое сопротивление теплопередачи через цилиндрическую стенку 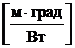
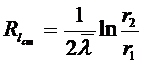 - термическое сопротивление теплопроводности стенки.
- термическое сопротивление теплопроводности стенки.
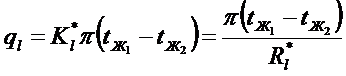
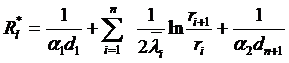 - линейное термическое сопротивление теплопередаче для многослойной цилиндрической стенки.
- линейное термическое сопротивление теплопередаче для многослойной цилиндрической стенки.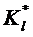 - линейный коэффициент теплопередачи через многослойную цилиндрическую стенку.
- линейный коэффициент теплопередачи через многослойную цилиндрическую стенку.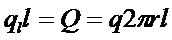
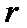 - любой текущий радиус:
- любой текущий радиус: 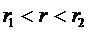
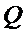 - передаваемое через поверхность тепло.
- передаваемое через поверхность тепло.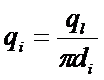 В нашем случае:
В нашем случае: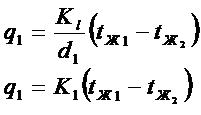
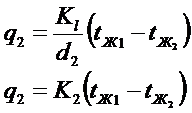
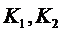 - коэффициенты теплопередачи, отнесённые к поверхности 1 или 2.
- коэффициенты теплопередачи, отнесённые к поверхности 1 или 2.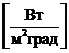
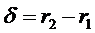 Возьмём
Возьмём 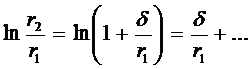 где
где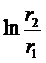 можно с достаточной точностью представить как первый член разложения, то это тонкая стенка.
можно с достаточной точностью представить как первый член разложения, то это тонкая стенка.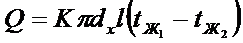 (*)
(*)
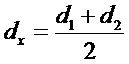
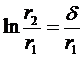 , запишем:
, запишем: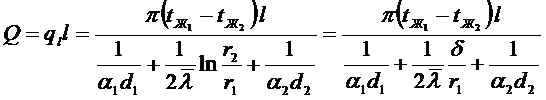
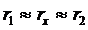 , то есть:
, то есть: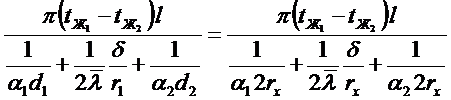

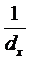 :
: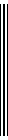

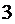

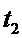
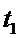






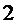


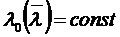
 Будем считать, что
Будем считать, что 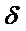 - известно,
- известно,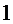
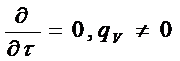
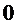
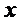

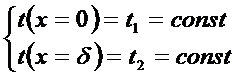
 - изотропные источники (равномерно распределённый по стенке),
- изотропные источники (равномерно распределённый по стенке), 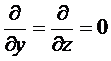
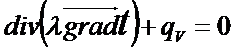
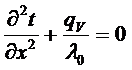 ;
; 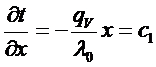 ;
;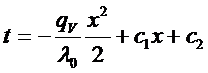
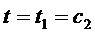


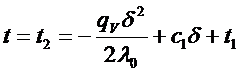
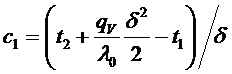
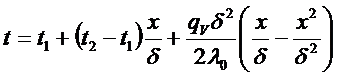
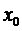
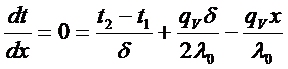

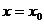
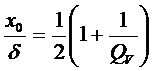


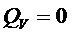
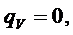
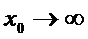 (экстремума нет)
(экстремума нет)