Кривая, заданная явным уравнением
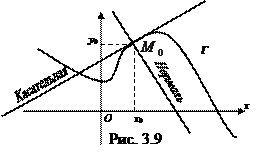
Уравнение касательной, проведенной к графику  функции
функции 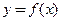 в точке
в точке 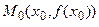 , в которой функция
, в которой функция  дифференцируема, имеет вид:
дифференцируема, имеет вид: 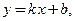 где
где 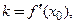
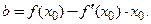 Таким образом,
Таким образом, 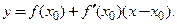 (3.29)
(3.29)
Прямая, проведенная через точку 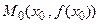 перпендикулярно к касательной, называется нормалью (см. рис. 3.9). Её уравнение при
перпендикулярно к касательной, называется нормалью (см. рис. 3.9). Её уравнение при 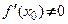 имеет вид:
имеет вид:
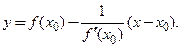 (3.30)
(3.30)
Здесь учтено, что у взаимно перпендикулярных наклонных прямых произведение угловых коэффициентов равно числу −1.
Часто вместо 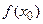 пишут
пишут 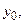 вместо
вместо 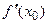 −
− 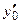 . Касательная и нормаль определены и в точках с бесконечной производной, где
. Касательная и нормаль определены и в точках с бесконечной производной, где 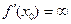 .
.
В зависимости от значения 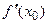 выделяют три случая.
выделяют три случая.
1. Если 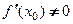 , то касательная и нормаль − наклонные прямые, описываемые уравнениями:
, то касательная и нормаль − наклонные прямые, описываемые уравнениями:
касательная: 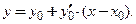 (3.31)
(3.31)
нормаль:  (3.32)
(3.32)
2. Если 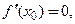 то касательная – горизонтальная прямая (горизонталь)
то касательная – горизонтальная прямая (горизонталь) 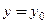 , нормаль – вертикальная прямая (вертикаль)
, нормаль – вертикальная прямая (вертикаль) 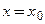 .
.
3. Если 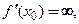 то касательная – вертикаль
то касательная – вертикаль 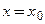 , нормаль – горизонталь
, нормаль – горизонталь 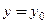 .
.
Чтобы составить уравнения касательной и нормали к графику функции 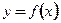 в точке
в точке 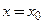 нужно определить три числа:
нужно определить три числа: 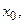
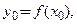
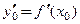 и подставить их значения в уравнения искомых линий, при этом целесообразно все данные собрать в таблице 3.3.
и подставить их значения в уравнения искомых линий, при этом целесообразно все данные собрать в таблице 3.3.
Табл. 3.3
Пример 3.26. Написать уравнения касательной и нормали к кривой, заданной уравнением 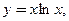 в точке, где а)
в точке, где а) 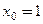 ; б)
; б) 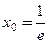 .
.
□ Найдем производную: 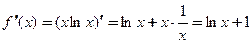 .
.
а) Вычислим  и
и 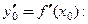
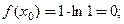
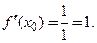 Заполним таблицу.
Заполним таблицу.
Так как производная в точке 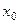 отлична от нуля, то имеет место 1-й случай. По формулам (3.31), (3.32) уравнение касательной:
отлична от нуля, то имеет место 1-й случай. По формулам (3.31), (3.32) уравнение касательной: 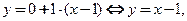 уравнение нормали:
уравнение нормали: 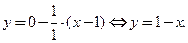
б) Вычислим  и
и 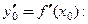
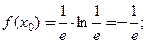
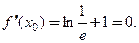 Заполним таблицу.
Заполним таблицу.
Так как производная в точке 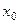 равна нулю, то имеет место 2-й случай. Касательная − горизонтальная прямая:
равна нулю, то имеет место 2-й случай. Касательная − горизонтальная прямая: 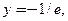 нормаль − вертикальная прямая:
нормаль − вертикальная прямая: 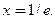 ■
■
Пример 3.27. Написать уравнения касательной и нормали к кривой, заданной уравнением 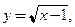 в точке, где а)
в точке, где а) 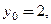 б)
б) 
□ В отличие от предыдущей задачи в этой задаче заданы ординаты точек касания.
а) Чтобы заполнить таблицу, сначала нужно найти 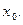 Составим уравнение:
Составим уравнение: 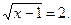 Его решением является число
Его решением является число 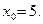 Потом находим
Потом находим 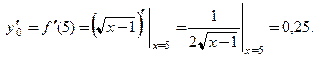
Соответствующая таблица имеет вид:
Применяем формулы (3.31) и (3.32), так как 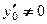 .
.
Касательная: 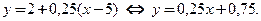
Нормаль: 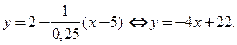
б) 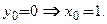 Точка
Точка 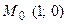 является граничной точкой области определения. В этой точке существует бесконечная правосторонняя производная:
является граничной точкой области определения. В этой точке существует бесконечная правосторонняя производная: 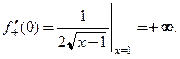 Следовательно, мы имеем дело с третьим случаем. Через точку
Следовательно, мы имеем дело с третьим случаем. Через точку 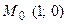 проходят вертикальная касательная
проходят вертикальная касательная 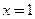 и нормаль
и нормаль 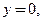 совпадающая с осью абсцисс.
совпадающая с осью абсцисс.
Кривая, заданная параметрическими уравнениями
Пусть кривая задана параметрическими уравнениями 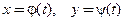 , точка
, точка 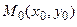 принадлежит графику Г функции. По аналогии с кривой, заданной явно, рассмотрим три случая. Вычисление
принадлежит графику Г функции. По аналогии с кривой, заданной явно, рассмотрим три случая. Вычисление 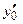 осуществим по формуле параметрического дифференцирования.
осуществим по формуле параметрического дифференцирования.
1. Если 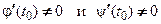 , то касательная и нормаль являются наклонными прямыми и их уравнения имеют вид:
, то касательная и нормаль являются наклонными прямыми и их уравнения имеют вид:
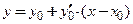 , (3.31)
, (3.31)
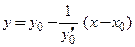 , (3.32)
, (3.32)
где 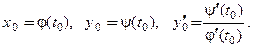 (3.33)
(3.33)
2. Если 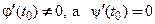 , то касательная и нормаль являются горизонталью и вертикалью, соответственно, и их уравнения имеют вид:
, то касательная и нормаль являются горизонталью и вертикалью, соответственно, и их уравнения имеют вид:
касательная: 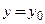 ,
,
нормаль: 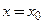 .
.
3. Если 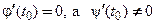 , то касательная и нормаль являются вертикалью и горизонталью, соответственно, и их уравнения имеют вид:
, то касательная и нормаль являются вертикалью и горизонталью, соответственно, и их уравнения имеют вид:
касательная: 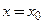 ,
,
нормаль: 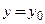 .
.
Пример 3.28. Написать уравнения касательной и нормали к кривой, заданной уравнениями 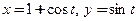 в точке, где а)
в точке, где а) 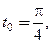 б)
б) 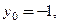 в)
в) 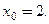
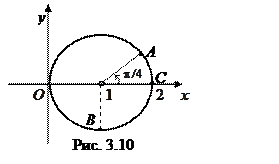 □ Заметим, что кривая, заданная уравнениями
□ Заметим, что кривая, заданная уравнениями 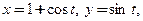 является окружностью единичного радиуса с центром, смещенным на единицу относительно точки О по оси абсцисс (см. рис. 3.10). Для обоснования утверждения достаточно уединить тригонометрические функции, возвести каждое уравнение в квадрат, после чего сложить их:
является окружностью единичного радиуса с центром, смещенным на единицу относительно точки О по оси абсцисс (см. рис. 3.10). Для обоснования утверждения достаточно уединить тригонометрические функции, возвести каждое уравнение в квадрат, после чего сложить их:

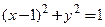
Последнее уравнение − уравнение окружности с центром в точке (1;0) и радиусом, равным 1. Исходные уравнения можно интерпретировать как закон перемещения материальной точки в плоскости 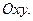 Производная, вычисленная в примере 3.16,
Производная, вычисленная в примере 3.16, 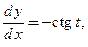 равна угловому коэффициенту касательной к траектории движения − окружности в произвольный момент времени
равна угловому коэффициенту касательной к траектории движения − окружности в произвольный момент времени 
а) Вычислим значения 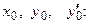
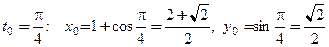 ,
, 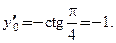 Производная
Производная 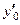 отлична от нуля, значит, имеет место первый случай.
отлична от нуля, значит, имеет место первый случай.
Заполним таблицу 3.3.
Подставляем найденные значения в уравнения (3.30) и (3.31) и получаем
касательную: 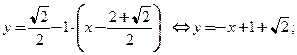
нормаль: 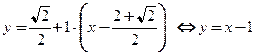 ,
,
проходящие через точку 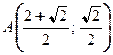 .
.
б) В задании указана только ордината точки касания. Чтобы найти все элементы уравнений касательной и нормали, решим тригонометрическое уравнение 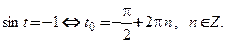 Отсюда
Отсюда 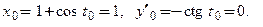 Так как производная
Так как производная 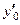 равна нулю, то имеет место второй случай. Касательная − горизонтальная прямая
равна нулю, то имеет место второй случай. Касательная − горизонтальная прямая 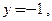 нормаль − вертикальная прямая, проходящие через точку
нормаль − вертикальная прямая, проходящие через точку 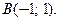
в) В задании указана только абсцисса точки касания. По аналогии с пунктом б) решим уравнение: 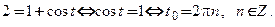 При этом значении
При этом значении 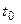
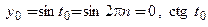 не определен, но существует
не определен, но существует 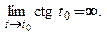 Имеет место третий случай. Отсюда следует, что через точку С (2; 0) проходит вертикальная касательная
Имеет место третий случай. Отсюда следует, что через точку С (2; 0) проходит вертикальная касательная 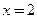 , а нормалью является горизонтальная прямая
, а нормалью является горизонтальная прямая 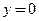 − ось абсцисс.
− ось абсцисс.
Полученные результаты имеют наглядный геометрический смысл. В пункте б) задания нужно было получить уравнения касательной и нормали в крайней нижней точке В заданной окружности с координатами (1; −1). Очевидно, что касательная и нормаль − это соответственно горизонтальная и вертикальная прямые, проходящие через точку (1; −1).
В пункте в) нужно было получить касательную и нормаль в крайней правой точке С заданной окружности с координатами (2;0). Очевидно, что касательной является вертикальная прямая, проходящая через точку (2;0), а нормалью − ось абсцисс.■
Угол между кривыми
Пусть 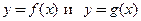 − уравнения линий в плоскости
− уравнения линий в плоскости 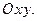 Углом
Углом 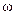 между этими линиями в точке их пересечения
между этими линиями в точке их пересечения 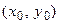 называют угол между касательными, проведенными к графикам функций в точке
называют угол между касательными, проведенными к графикам функций в точке 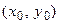 .
.
Если функции 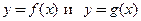 дифференцируемы в точке
дифференцируемы в точке 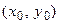 , то угол
, то угол 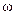 можно найти из тригонометрического уравнения:
можно найти из тригонометрического уравнения:
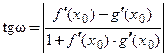 . (3.34)
. (3.34)
Пример 3.29. Найти угол между кривыми, заданными уравнениями 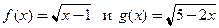 , в точке их пересечения.
, в точке их пересечения.
□ 1. Найдем точку пересечения графиков из системы: 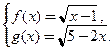 Уравнение
Уравнение 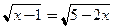 имеет единственное решение
имеет единственное решение 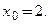 Тогда
Тогда 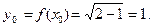 Точка пересечения графиков имеет координаты
Точка пересечения графиков имеет координаты 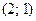 .
.
2. Найдем производные функций: 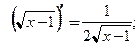
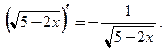
3. Вычислим значения производных в точке, где 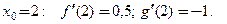
4. Составим и решим уравнение относительно угла 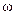 :
:
 ■
■
Правило Лопиталя-Бернулли
Теорема 3.13 (правило Лопиталя-Бернулли) .Если выполняются следующие условия:
1) функции  и
и 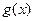 определены и дифференцируемы в проколотой окрестности точки
определены и дифференцируемы в проколотой окрестности точки  ;
;
2) 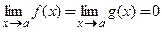 ;
;
3) 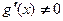 в рассматриваемой окрестности;
в рассматриваемой окрестности;
4) существует предел 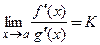 ,
,
то
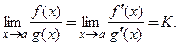 (3.35)
(3.35)
З а м е ч а н и е 1. Это правило применимо для раскрытия неопределенностей вида  :
:
● в конечной точке при 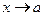 ,
,
● на бесконечности при 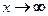 ;
;
● при вычислении односторонних пределов (при 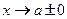 и
и 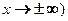 .
.
З а м е ч а н и е 2. Аналогичное правило применимо для раскрытия неопределенностей вида 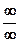 , при этом в условиях теоремы 3.13 нужно изменить только второе условие и потребовать, чтобы
, при этом в условиях теоремы 3.13 нужно изменить только второе условие и потребовать, чтобы 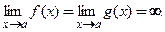 Все пункты замечания 1 и в этом случае верны.
Все пункты замечания 1 и в этом случае верны.
Теорему 3.13 для раскрытия неопределенности 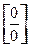 часто называют первым правилом Лопиталя, а аналогичную теорему для неопределенности вида
часто называют первым правилом Лопиталя, а аналогичную теорему для неопределенности вида 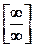 − вторым правилом Лопиталя.
− вторым правилом Лопиталя.
Пример 3.30. Найти пределы: а) 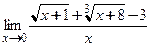 ; б)
; б) 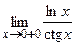 ; в)
; в) 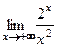 .
.
□ В каждом примере при подстановке предельного значения аргумента получается неопределенное выражение, которое раскрывается путем однократного или многократного непосредственного применения правила Лопиталя.
а) 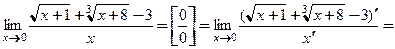
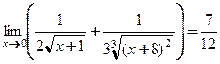 .
.
б) 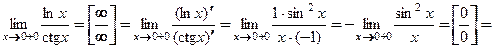
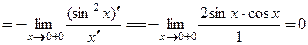 .
.
в) 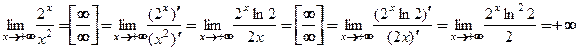 .■
.■
Пример 3.31. Найти 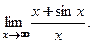
□ При 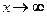 числитель и знаменатель дроби
числитель и знаменатель дроби 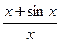 неограниченно растут. Вычисление предела связано с раскрытием неопределенности вида
неограниченно растут. Вычисление предела связано с раскрытием неопределенности вида 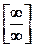 . Однако воспользоваться правилом Лопиталя нельзя, так как не существует предела
. Однако воспользоваться правилом Лопиталя нельзя, так как не существует предела 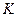 отношения производных:
отношения производных: 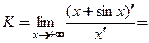
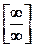 =
= 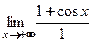 . Как известно, функция
. Как известно, функция  на бесконечности не имеет предела и вместе с ней нет предела у функции
на бесконечности не имеет предела и вместе с ней нет предела у функции 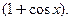
Предел можно найти другим способом: 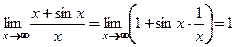 , так как предел второго слагаемого как предел произведения ограниченной функции (
, так как предел второго слагаемого как предел произведения ограниченной функции (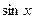 ) и бесконечно малой при
) и бесконечно малой при  функции
функции 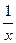 равен нулю, а предел всей суммы − единице. ■
равен нулю, а предел всей суммы − единице. ■
Для раскрытия неопределенностей вида 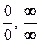 правила Лопиталя применяют непосредственно. Для раскрытия неопределенностей вида
правила Лопиталя применяют непосредственно. Для раскрытия неопределенностей вида 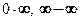 ,
, 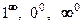 правила Лопиталя применяют опосредованно:
правила Лопиталя применяют опосредованно:
1) в случае неопределенности вида 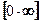 произведение функций преобразуют в частное одним из двух способов:
произведение функций преобразуют в частное одним из двух способов: 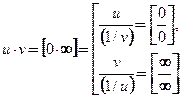 ;
;
2) в случае неопределенности вида 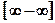 разность функций преобразуют в
разность функций преобразуют в
частное, используя свойства функций или следующий общий прием:
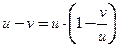 при
при 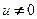 , или
, или 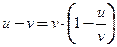 , причем
, причем
● если предел 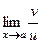 существует и отличен от единицы:
существует и отличен от единицы: 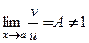 , то
, то 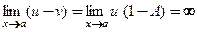 ;
;
● если предел 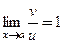 , то
, то 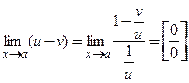 и далее непосредственно применяют правило Лопиталя-Бернулли;
и далее непосредственно применяют правило Лопиталя-Бернулли;
3) в случае неопределенностей вида 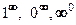 используют основное свойство логарифма
используют основное свойство логарифма 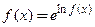 и неопределенность
и неопределенность 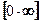 в показателе степени раскрывают при помощи вышеописанных приемов.
в показателе степени раскрывают при помощи вышеописанных приемов.
Пример 3.32. Найти 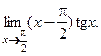 .
.
□ Выясним, есть ли неопределенность при вычислении предела: 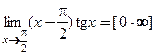 . Как видим, мы имеем дело с 1-ым случаем опосредованного применения правила Лопиталя. Преобразовываем произведение в частное и применяем 1-ое правило Лопиталя:
. Как видим, мы имеем дело с 1-ым случаем опосредованного применения правила Лопиталя. Преобразовываем произведение в частное и применяем 1-ое правило Лопиталя: 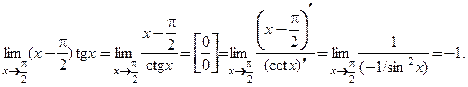 ■
■
Найдем 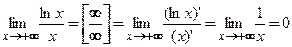 .
.
Тогда 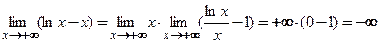 .
.
Пример 3.33. Найти  .
.
□ Здесь неопределенность вида 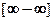 . Используем общий прием преобразования разности в частное:
. Используем общий прием преобразования разности в частное: 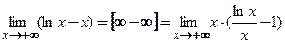 .
.
Найдем 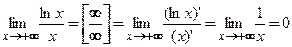 .
.
Тогда 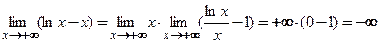 .
.
Заметим, что другой способ преобразования разности в произведение, а именно, вынесение  вместо
вместо  вперед в качестве множителя приведет к тому же результату. ■
вперед в качестве множителя приведет к тому же результату. ■
Пример 3.34. Найти 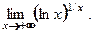
□ 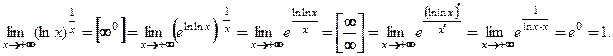 ■
■
Задачи для самостоятельного решения
1. Используя формулу Маклорена 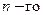 порядка, найдите приближенное значение
порядка, найдите приближенное значение 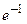 и оцените абсолютную погрешность, если:
и оцените абсолютную погрешность, если:
1) 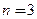 ; 2)
; 2) 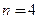 .
.
Ответы: 1)0,3 и 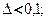 2)
2) 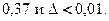
2. Найдите приближенное значение 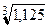 и оцените абсолютные погрешности:
и оцените абсолютные погрешности:
1) при помощи первого дифференциала; 2) при помощи формулы конечных приращений;
3) при помощи формулы Тейлора 2-го порядка.
Ответы: 1)1,041(6); 2) 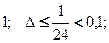 3)
3) 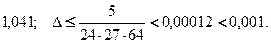
3. Составьте уравнения касательной и нормали к графику заданной функции  в заданной точке
в заданной точке 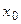 :
:
1) 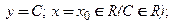 2)
2) 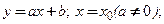 3)
3) 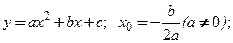
4) 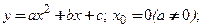 5)
5) 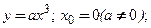 6)
6) 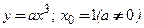 .
.
Ответы: 1) 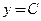 ,
, 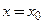 ; 2)
; 2)  ,
, 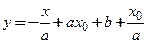 ; 3)
; 3) 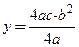 ,
, 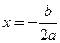 ;
;
4) 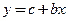 ,
, 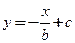 ; 5)
; 5) 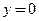 ,
, 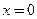 ; 6)
; 6) 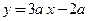 ,
, 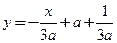 .
.
4. Составьте уравнения касательной и нормали к графику 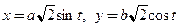 в точке, где
в точке, где 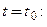 1)
1)  2)
2) 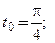 3)
3) 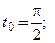 4)
4) 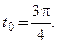
Ответы (уравнения касательной и нормали): 1) 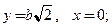
2) 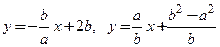 ; 3)
; 3) 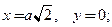 4)
4) 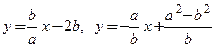 .
.
5. Найдите углы между графиками функций 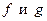 в точке их пересечения:
в точке их пересечения:
1) 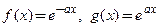 ; 2)
; 2) 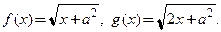
Ответы: 1) 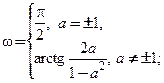 2)
2) 
6. Укажите вид неопределенности и найдите пределы (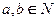 )
)
1) 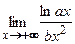 ; 2)
; 2) 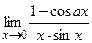 ; 3)
; 3) 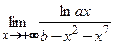 ; 4)
; 4) 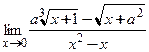 ;
;
5) 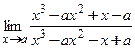 ; 6)
; 6) 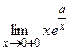 ; 7)
; 7)  ; 8)
; 8) 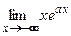 ; 9)
; 9) 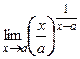 ;
;
10) 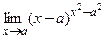 ; 11)
; 11) 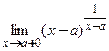 ; 12)
; 12) 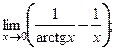 13)
13) 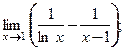
14) 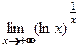 ; 15)
; 15) 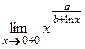 .
.
Ответы: 1) 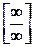 , 0; 2)
, 0; 2) 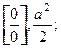 3)
3) 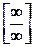 ,0; 4)
,0; 4) 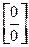 ,
, 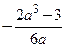 ; 5)
; 5) 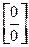 ,
, 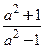 ; 6)
; 6) 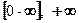 ;
;
7) 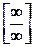 ,
, 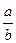 ; 8)
; 8) 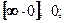 9)
9) 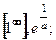 10)
10) 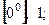 11)
11) 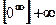 ; 12)
; 12) 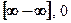 ; 13)
; 13) 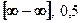 ; 14)
; 14)  ; 15)
; 15) 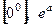 .
.



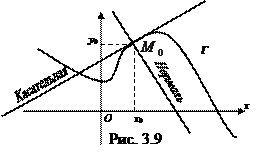
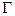 функции
функции 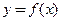 в точке
в точке 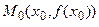 , в которой функция
, в которой функция  дифференцируема, имеет вид:
дифференцируема, имеет вид: 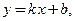 где
где 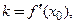
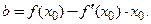 Таким образом,
Таким образом, 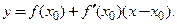 (3.29)
(3.29)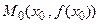 перпендикулярно к касательной, называется нормалью (см. рис. 3.9). Её уравнение при
перпендикулярно к касательной, называется нормалью (см. рис. 3.9). Её уравнение при 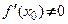 имеет вид:
имеет вид: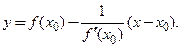 (3.30)
(3.30)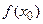 пишут
пишут 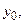 вместо
вместо 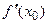 −
− 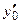 . Касательная и нормаль определены и в точках с бесконечной производной, где
. Касательная и нормаль определены и в точках с бесконечной производной, где 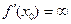 .
.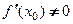 , то касательная и нормаль − наклонные прямые, описываемые уравнениями:
, то касательная и нормаль − наклонные прямые, описываемые уравнениями: 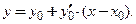 (3.31)
(3.31) (3.32)
(3.32)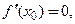 то касательная – горизонтальная прямая (горизонталь)
то касательная – горизонтальная прямая (горизонталь) 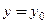 , нормаль – вертикальная прямая (вертикаль)
, нормаль – вертикальная прямая (вертикаль) 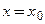 .
.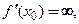 то касательная – вертикаль
то касательная – вертикаль 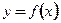 в точке
в точке 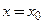 нужно определить три числа:
нужно определить три числа: 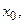
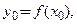
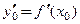 и подставить их значения в уравнения искомых линий, при этом целесообразно все данные собрать в таблице 3.3.
и подставить их значения в уравнения искомых линий, при этом целесообразно все данные собрать в таблице 3.3.
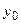
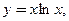 в точке, где а)
в точке, где а) 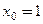 ; б)
; б) 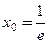 .
.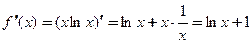 .
. и
и 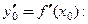
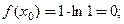
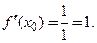 Заполним таблицу.
Заполним таблицу.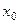 отлична от нуля, то имеет место 1-й случай. По формулам (3.31), (3.32) уравнение касательной:
отлична от нуля, то имеет место 1-й случай. По формулам (3.31), (3.32) уравнение касательной: 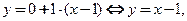 уравнение нормали:
уравнение нормали: 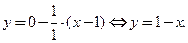
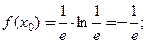
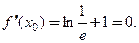 Заполним таблицу.
Заполним таблицу.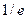
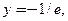 нормаль − вертикальная прямая:
нормаль − вертикальная прямая: 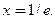 ■
■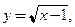 в точке, где а)
в точке, где а) 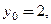 б)
б) 
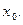 Составим уравнение:
Составим уравнение: 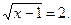 Его решением является число
Его решением является число 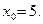 Потом находим
Потом находим 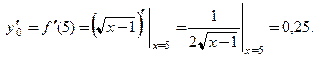
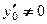 .
.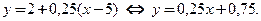
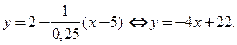
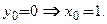 Точка
Точка 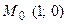 является граничной точкой области определения. В этой точке существует бесконечная правосторонняя производная:
является граничной точкой области определения. В этой точке существует бесконечная правосторонняя производная: 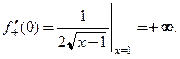 Следовательно, мы имеем дело с третьим случаем. Через точку
Следовательно, мы имеем дело с третьим случаем. Через точку 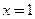 и нормаль
и нормаль 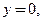 совпадающая с осью абсцисс.
совпадающая с осью абсцисс.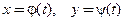 , точка
, точка 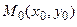 принадлежит графику Г функции. По аналогии с кривой, заданной явно, рассмотрим три случая. Вычисление
принадлежит графику Г функции. По аналогии с кривой, заданной явно, рассмотрим три случая. Вычисление 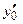 осуществим по формуле параметрического дифференцирования.
осуществим по формуле параметрического дифференцирования.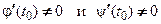 , то касательная и нормаль являются наклонными прямыми и их уравнения имеют вид:
, то касательная и нормаль являются наклонными прямыми и их уравнения имеют вид: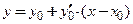 , (3.31)
, (3.31)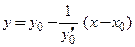 , (3.32)
, (3.32)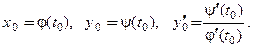 (3.33)
(3.33)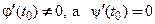 , то касательная и нормаль являются горизонталью и вертикалью, соответственно, и их уравнения имеют вид:
, то касательная и нормаль являются горизонталью и вертикалью, соответственно, и их уравнения имеют вид: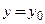 ,
, 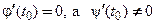 , то касательная и нормаль являются вертикалью и горизонталью, соответственно, и их уравнения имеют вид:
, то касательная и нормаль являются вертикалью и горизонталью, соответственно, и их уравнения имеют вид: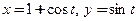 в точке, где а)
в точке, где а) 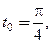 б)
б) 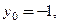 в)
в) 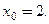
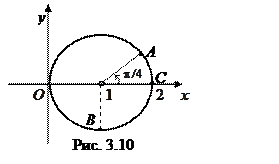 □ Заметим, что кривая, заданная уравнениями
□ Заметим, что кривая, заданная уравнениями 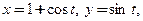 является окружностью единичного радиуса с центром, смещенным на единицу относительно точки О по оси абсцисс (см. рис. 3.10). Для обоснования утверждения достаточно уединить тригонометрические функции, возвести каждое уравнение в квадрат, после чего сложить их:
является окружностью единичного радиуса с центром, смещенным на единицу относительно точки О по оси абсцисс (см. рис. 3.10). Для обоснования утверждения достаточно уединить тригонометрические функции, возвести каждое уравнение в квадрат, после чего сложить их:
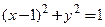
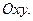 Производная, вычисленная в примере 3.16,
Производная, вычисленная в примере 3.16, 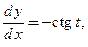 равна угловому коэффициенту касательной к траектории движения − окружности в произвольный момент времени
равна угловому коэффициенту касательной к траектории движения − окружности в произвольный момент времени 
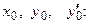
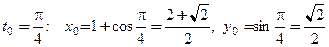 ,
, 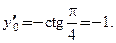 Производная
Производная 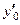 отлична от нуля, значит, имеет место первый случай.
отлична от нуля, значит, имеет место первый случай.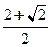
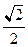
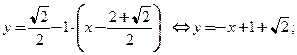
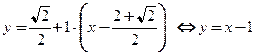 ,
,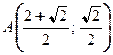 .
. 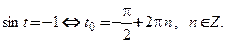 Отсюда
Отсюда 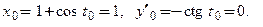 Так как производная
Так как производная 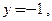 нормаль − вертикальная прямая, проходящие через точку
нормаль − вертикальная прямая, проходящие через точку 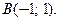
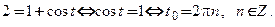 При этом значении
При этом значении 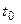
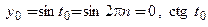 не определен, но существует
не определен, но существует 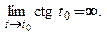 Имеет место третий случай. Отсюда следует, что через точку С (2; 0) проходит вертикальная касательная
Имеет место третий случай. Отсюда следует, что через точку С (2; 0) проходит вертикальная касательная 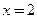 , а нормалью является горизонтальная прямая
, а нормалью является горизонтальная прямая 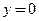 − ось абсцисс.
− ось абсцисс.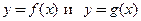 − уравнения линий в плоскости
− уравнения линий в плоскости 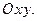 Углом
Углом 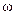 между этими линиями в точке их пересечения
между этими линиями в точке их пересечения 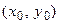 называют угол между касательными, проведенными к графикам функций в точке
называют угол между касательными, проведенными к графикам функций в точке 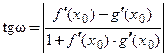 . (3.34)
. (3.34)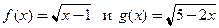 , в точке их пересечения.
, в точке их пересечения.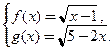 Уравнение
Уравнение 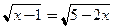 имеет единственное решение
имеет единственное решение 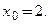 Тогда
Тогда 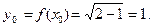 Точка пересечения графиков имеет координаты
Точка пересечения графиков имеет координаты 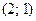 .
.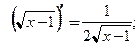
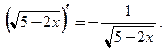
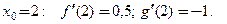
 ■
■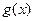 определены и дифференцируемы в проколотой окрестности точки
определены и дифференцируемы в проколотой окрестности точки  ;
;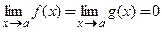 ;
;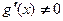 в рассматриваемой окрестности;
в рассматриваемой окрестности;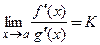 ,
,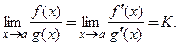 (3.35)
(3.35) :
: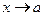 ,
,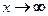 ;
;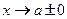 и
и 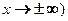 .
.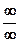 , при этом в условиях теоремы 3.13 нужно изменить только второе условие и потребовать, чтобы
, при этом в условиях теоремы 3.13 нужно изменить только второе условие и потребовать, чтобы 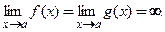 Все пункты замечания 1 и в этом случае верны.
Все пункты замечания 1 и в этом случае верны.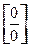 часто называют первым правилом Лопиталя, а аналогичную теорему для неопределенности вида
часто называют первым правилом Лопиталя, а аналогичную теорему для неопределенности вида 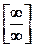 − вторым правилом Лопиталя.
− вторым правилом Лопиталя.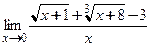 ; б)
; б) 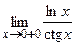 ; в)
; в) 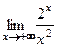 .
.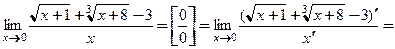
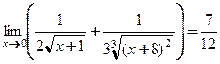 .
.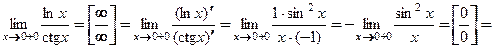
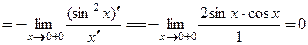 .
.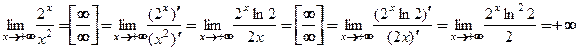 .■
.■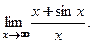
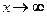 числитель и знаменатель дроби
числитель и знаменатель дроби 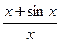 неограниченно растут. Вычисление предела связано с раскрытием неопределенности вида
неограниченно растут. Вычисление предела связано с раскрытием неопределенности вида 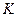 отношения производных:
отношения производных: 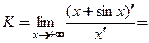
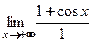 . Как известно, функция
. Как известно, функция  на бесконечности не имеет предела и вместе с ней нет предела у функции
на бесконечности не имеет предела и вместе с ней нет предела у функции 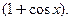
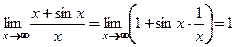 , так как предел второго слагаемого как предел произведения ограниченной функции (
, так как предел второго слагаемого как предел произведения ограниченной функции (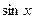 ) и бесконечно малой при
) и бесконечно малой при  функции
функции 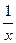 равен нулю, а предел всей суммы − единице. ■
равен нулю, а предел всей суммы − единице. ■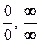 правила Лопиталя применяют непосредственно. Для раскрытия неопределенностей вида
правила Лопиталя применяют непосредственно. Для раскрытия неопределенностей вида 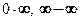 ,
, 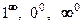 правила Лопиталя применяют опосредованно:
правила Лопиталя применяют опосредованно: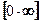 произведение функций преобразуют в частное одним из двух способов:
произведение функций преобразуют в частное одним из двух способов: 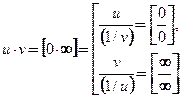 ;
;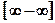 разность функций преобразуют в
разность функций преобразуют в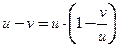 при
при 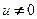 , или
, или 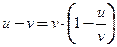 , причем
, причем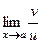 существует и отличен от единицы:
существует и отличен от единицы: 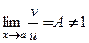 , то
, то 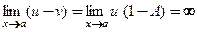 ;
; 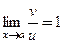 , то
, то 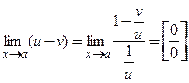 и далее непосредственно применяют правило Лопиталя-Бернулли;
и далее непосредственно применяют правило Лопиталя-Бернулли;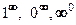 используют основное свойство логарифма
используют основное свойство логарифма 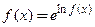 и неопределенность
и неопределенность 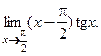 .
.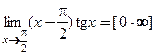 . Как видим, мы имеем дело с 1-ым случаем опосредованного применения правила Лопиталя. Преобразовываем произведение в частное и применяем 1-ое правило Лопиталя:
. Как видим, мы имеем дело с 1-ым случаем опосредованного применения правила Лопиталя. Преобразовываем произведение в частное и применяем 1-ое правило Лопиталя: 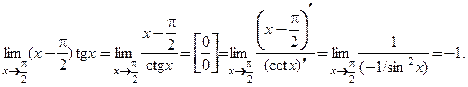 ■
■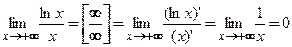 .
.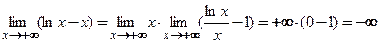 .
. .
.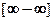 . Используем общий прием преобразования разности в частное:
. Используем общий прием преобразования разности в частное: 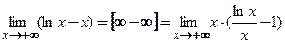 .
. вместо
вместо  вперед в качестве множителя приведет к тому же результату. ■
вперед в качестве множителя приведет к тому же результату. ■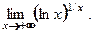
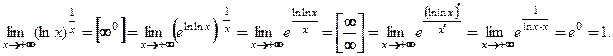 ■
■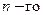 порядка, найдите приближенное значение
порядка, найдите приближенное значение 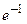 и оцените абсолютную погрешность, если:
и оцените абсолютную погрешность, если: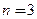 ; 2)
; 2) 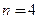 .
. 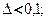 2)
2) 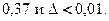
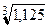 и оцените абсолютные погрешности:
и оцените абсолютные погрешности: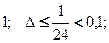 3)
3) 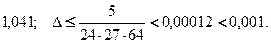
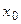 :
: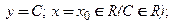 2)
2) 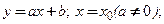 3)
3) 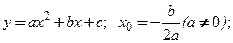
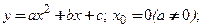 5)
5) 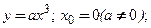 6)
6) 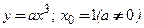 .
.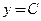 ,
,  ,
, 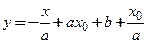 ; 3)
; 3) 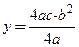 ,
, 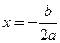 ;
;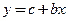 ,
, 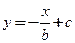 ; 5)
; 5) 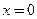 ; 6)
; 6) 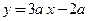 ,
, 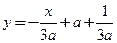 .
.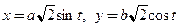 в точке, где
в точке, где 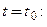 1)
1)  2)
2) 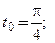 3)
3) 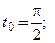 4)
4) 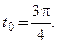
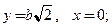
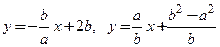 ; 3)
; 3) 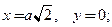 4)
4) 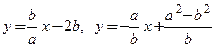 .
.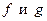 в точке их пересечения:
в точке их пересечения: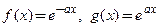 ; 2)
; 2) 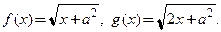
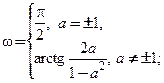 2)
2) 
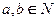 )
)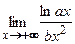 ; 2)
; 2) 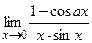 ; 3)
; 3) 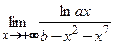 ; 4)
; 4) 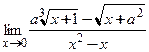 ;
;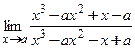 ; 6)
; 6) 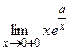 ; 7)
; 7)  ; 8)
; 8) 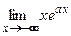 ; 9)
; 9) 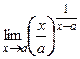 ;
;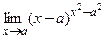 ; 11)
; 11) 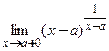 ; 12)
; 12) 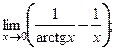 13)
13) 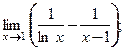
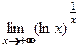 ; 15)
; 15) 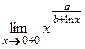 .
.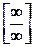 , 0; 2)
, 0; 2) 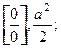 3)
3) 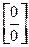 ,
, 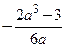 ; 5)
; 5) 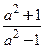 ; 6)
; 6) 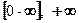 ;
;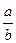 ; 8)
; 8) 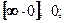 9)
9) 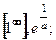 10)
10) 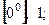 11)
11) 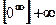 ; 12)
; 12) 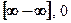 ; 13)
; 13) 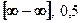 ; 14)
; 14)  ; 15)
; 15) 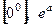 .
.


