ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 133
3.1. Производная и дифференциал функции одной переменной. Основные понятия.... 133
3.1.1. Определения и условия существования производной и дифференциала ………133
3.1.2. Смысл производной и дифференциала.................................................................. 137
3.2. Основные приемы дифференцирования.................................................................... 142
3.2.1. Табличное дифференцирование............................................................................. 142
3.2.2. Общие правила дифференцирования.................................................................... 143
3.2.3. Дифференцирование сложной и неявной функции. Инвариантное
свойство дифференциала……….... …................................................................... 144
3.2.4. Дифференцирование обратной функции............................................................. 146
3.2.5. Логарифмическое дифференцирование. Темп роста и эластичность функции 146
3.2.6. Параметрическое дифференцирование............................................................... 148
3.3. Производные и дифференциалы высших порядков…………………………….... 152
3.3.1. Дифференцирование явной функции.................. …………………………………… .152
3.3.2 Производные высших порядков некоторых элементарных функций. Формула
Лейбница........................................................... ……………………………………155
3.3.3. Параметрическое дифференцирование................................................................ 156
3.4. Основные теоремы дифференциального исчисления............................................. 159
3.4.1. Теоремы о среднем (Ферма, Ролля, Коши, Лагранжа)......................................... 159
3.4.2. Формула Тейлора...................................................................................................... 160
3.4.3. Формулы Маклорена для некоторых элементарных функций........................... 163
3.5. Приложения дифференциального исчисления........................................................ 165
3.5.1 Приближенное вычисление значений функции................................................... 165
3.5.2. Составление уравнений касательной и нормали к кривой...... …………………167
3.5.3. Правило Лопиталя-Бернулли................................................................................... 171
3.6. Исследование функции.................................................................................................... 176
3.6.1. Промежутки монотонности и точки экстремума…….......................................... 176
3.6.2. Промежутки выпуклости и точки перегиба........................................................... 180
3.6.3. Асимптоты графика функции.................................................................................. 183
3.6.4. Общая схема исследования функции и построения графика............................... 185
3.6.5. Наибольшее и наименьшее значения функции …… ……………………… 190
3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Дифференцирование функции одной переменной
Определения и условия существования производной и дифференциала
Рассмотрим функцию 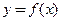 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки 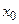 . Дадим аргументу
. Дадим аргументу  такое приращение
такое приращение 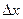 , что точка
, что точка 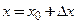 также принадлежит рассматриваемой окрестности. Соответствующее приращение функции
также принадлежит рассматриваемой окрестности. Соответствующее приращение функции 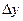 равно:
равно:  , или
, или 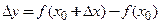 . Приращение функции
. Приращение функции 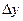 зависит и от
зависит и от 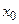 , и от приращения аргумента
, и от приращения аргумента 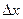 , что иногда подчеркивают записью
, что иногда подчеркивают записью  .
.
Производной 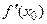 функции
функции  в точке
в точке 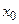 называют предел отношения приращения функции
называют предел отношения приращения функции 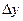 к приращению аргумента
к приращению аргумента 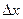
 при стремлении последнего к нулю:
при стремлении последнего к нулю:
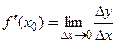 . (3.1)
. (3.1)
Для обозначения производной используют и другие символы: 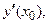

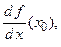
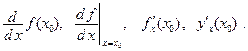 Производная может быть как конечной, так и бесконечной величиной. Если предел (3.1) не существует, то и производная
Производная может быть как конечной, так и бесконечной величиной. Если предел (3.1) не существует, то и производная 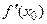 не существует.
не существует.
Операцию вычисления производной функции называют дифференцированием функции.
Односторонние производные функции  в точке
в точке 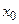 соответственно равны:
соответственно равны:
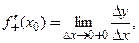
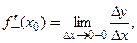
где  и
и 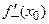 − правосторонняя (правая) и левосторонняя (левая) производная в точке
− правосторонняя (правая) и левосторонняя (левая) производная в точке 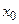 . При записи правосторонней и левосторонней производной используют и такие обозначения:
. При записи правосторонней и левосторонней производной используют и такие обозначения: 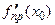 и
и  . В граничных точках отрезков можно определить только односторонние производные.
. В граничных точках отрезков можно определить только односторонние производные.
Если функция  определена на некотором промежутке
определена на некотором промежутке 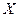 и ее производная существует при каждом значении
и ее производная существует при каждом значении 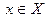 , то формула
, то формула 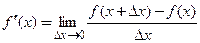 определяет производную как функцию аргумента
определяет производную как функцию аргумента  при
при 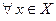 .
.
Теорема 3.1 (критерий существования производной в точке). Чтобы функция  имела производную
имела производную 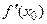 в точке
в точке 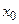 , необходимо и достаточно, чтобы существовали равные односторонние производные
, необходимо и достаточно, чтобы существовали равные односторонние производные  и
и 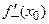 . При этом имеет место равенство:
. При этом имеет место равенство: 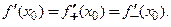
Теорема 3.2 (необходимое условие существования конечной производной функции в точке). Если функция имеет конечную производную в некоторой точке, то функция непрерывна в этой точке:
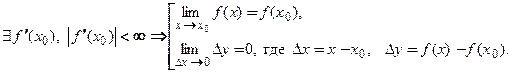
Следствие теоремы 3.2. Если функция разрывна в точке 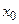 , то она не имеет конечной производной в этой точке.
, то она не имеет конечной производной в этой точке.
Пример 3.1. Найти производную 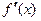 , если
, если  .
.
’ Функцию 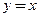 называют идентичной функцией.
называют идентичной функцией.
Поскольку область определения этой функции  , то
, то 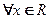 можно определить приращение функции
можно определить приращение функции 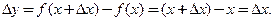
Тогда согласно (3.1) 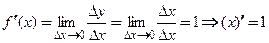 . ■
. ■
Пример 3.2. Найти  , если
, если 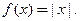
’ Область определения функции  . По определению модуля
. По определению модуля
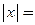
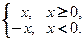
При  и
и 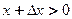
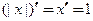 (см. пример 3.1).
(см. пример 3.1).
При  и
и 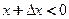 приращение функции равно:
приращение функции равно: 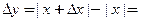
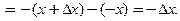 Отсюда, при
Отсюда, при 
 Тогда
Тогда 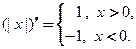
Рассмотрим данную функцию в окрестности точки 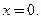 Найдем односторонние производные в этой точке:
Найдем односторонние производные в этой точке:
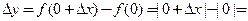
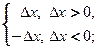
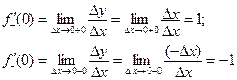
 не существует согласно теореме 3.1.
не существует согласно теореме 3.1.
Функция 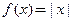 является примером функции, определенной и непрерывной на множестве
является примером функции, определенной и непрерывной на множестве  и имеющей производную на всей оси, кроме точки
и имеющей производную на всей оси, кроме точки 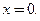 ■
■
Пример 3.3. Найти 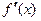 , если
, если 
‚ Область определения  функции
функции  − это полуось
− это полуось  . Для
. Для 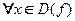 можно определить приращение функции
можно определить приращение функции 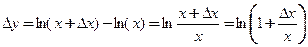 , если
, если
точка  Тогда согласно (3.1)
Тогда согласно (3.1) 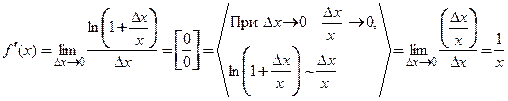 .
.
Итак, 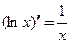
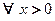 . ■
. ■
Пример 3.4. Найти 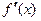 , если
, если 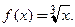
‚ Область определения функции 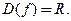 Для любого
Для любого 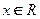 можно определить приращение функции
можно определить приращение функции 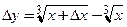 . Для удобства последующих вычислений преобразуем его:
. Для удобства последующих вычислений преобразуем его:
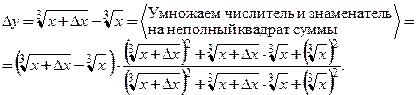
Используем формулу для разности кубов 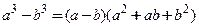 и получаем
и получаем
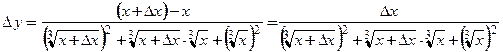 .
.
Тогда согласно (3.1)
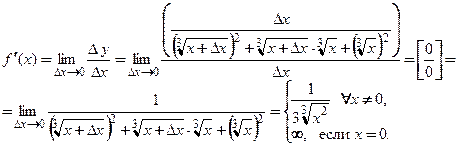
Значит, 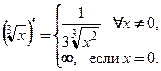
Функция 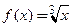 является примером функции определенной, непрерывной и имеющей производную на множестве
является примером функции определенной, непрерывной и имеющей производную на множестве 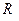 . Производная функции конечна во всех точках множества
. Производная функции конечна во всех точках множества 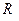 , кроме
, кроме 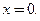 Производная бесконечна при
Производная бесконечна при 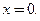 ■
■
Пример 3.5. Найти 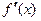 , если функция
, если функция 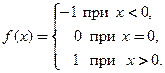
□ Кусочно-заданная функция  определена на всей числовой оси и является непрерывной во всех точках оси, кроме
определена на всей числовой оси и является непрерывной во всех точках оси, кроме 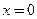 . В силу следствия из теоремы 3.2 в этой точке у функции нет конечной производной, так как точка
. В силу следствия из теоремы 3.2 в этой точке у функции нет конечной производной, так как точка 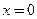 является точкой разрыва 1-го рода:
является точкой разрыва 1-го рода: 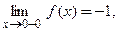
 и эти три числа не равны между собой.
и эти три числа не равны между собой.
При  производная этой функции равна нулю:
производная этой функции равна нулю: 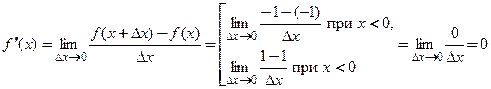 .
.
Найдем односторонние производные в точке  :
:
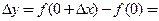
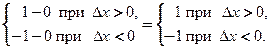


Обе односторонние производные бесконечны в точке 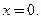 Значит, в этой точке существует бесконечная производная
Значит, в этой точке существует бесконечная производная 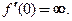 ■
■
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 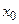 , если ее приращение представимо в виде:
, если ее приращение представимо в виде:
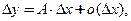 (3.2)
(3.2)
где 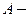 конечная величина, не зависящая от
конечная величина, не зависящая от 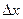 ;
; 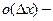 бесконечно малая величина высшего порядка малости относительно
бесконечно малая величина высшего порядка малости относительно 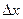 при
при 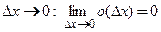 и
и 
Главная линейная относительно 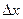 часть приращения дифференцируемой в точке
часть приращения дифференцируемой в точке 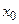 функции, равная
функции, равная 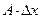 , называется дифференциалом функции и обозначается
, называется дифференциалом функции и обозначается 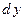 . Наряду с этим обозначением дифференциала используют и другие:
. Наряду с этим обозначением дифференциала используют и другие: 
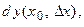
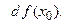
Тогда формулу (3.2) можно переписать в виде:
 (3.3)
(3.3)
В приближенных вычислениях отбрасывают слагаемое 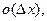 полагая его малой величиной, и приращение
полагая его малой величиной, и приращение 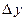 заменяют дифференциалом
заменяют дифференциалом 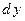 :
:
 (3.4)
(3.4)
Теорема 3.3. Чтобы функция  была дифференцируемой в точке
была дифференцируемой в точке 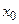 , необходимо и достаточно, чтобы существовала конечная производная
, необходимо и достаточно, чтобы существовала конечная производная 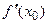 , при этом
, при этом
 , или кратко
, или кратко 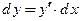 , (3.5)
, (3.5)
где 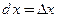 для независимой переменной
для независимой переменной 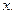
Отсюда следует, что производная  является отношением дифференциалов
является отношением дифференциалов 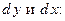
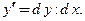 Значит, запись
Значит, запись  является не только обозначением производной, но и формулой для ее нахождения. Заметим, что теорема верна и для граничных точек отрезка, если под производной понимать одностороннюю производную.
является не только обозначением производной, но и формулой для ее нахождения. Заметим, что теорема верна и для граничных точек отрезка, если под производной понимать одностороннюю производную.
Операцию вычисления дифференциала функции так же, как и операцию вычисления производной, называют дифференцированием функции.
Функция  называется дифференцируемой на промежутке
называется дифференцируемой на промежутке 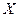 если она дифференцируема в каждой точке этого промежутка.
если она дифференцируема в каждой точке этого промежутка.
Приведем комментарии к результатам, полученным в примерах 3.1−3.5.
● Функция 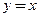 дифференцируема по теореме 3.3 в любой точке числовой оси, поскольку её производная
дифференцируема по теореме 3.3 в любой точке числовой оси, поскольку её производная 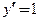 , т.е. производная существует и конечна при любых значениях
, т.е. производная существует и конечна при любых значениях  ; при этом
; при этом  при любом
при любом 
● Функция 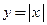 дифференцируема по теореме 3.3 при любых значениях
дифференцируема по теореме 3.3 при любых значениях  , кроме
, кроме 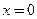 . При этом
. При этом 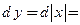
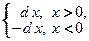 . При
. При 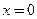
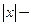 недифференцируемая функция, так как в этой точке производная не существует.
недифференцируемая функция, так как в этой точке производная не существует.
● Функция  дифференцируема по теореме 3.3 при любом положительном
дифференцируема по теореме 3.3 при любом положительном
значении  и
и 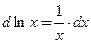 .
.
● Функция 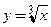 дифференцируема по теореме 3.3 при любых значениях
дифференцируема по теореме 3.3 при любых значениях  , кроме
, кроме 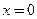 . При этом
. При этом 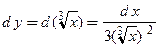 при
при 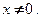 При
При 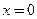
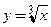 − недифференцируемая функция, так как в этой точке производная обращается в бесконечность.
− недифференцируемая функция, так как в этой точке производная обращается в бесконечность.
● Функция 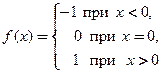 дифференцируема по теореме 3.3 при
дифференцируема по теореме 3.3 при  , при этом
, при этом 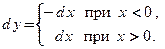 Функция
Функция  не дифференцируема в точке
не дифференцируема в точке 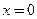 , так как в этой точке не существует конечная производная.
, так как в этой точке не существует конечная производная.
3.1.2. Смысл производной и дифференциала
Геометрический смысл производной и дифференциала
Конечная производная. Рассмотрим функцию

, непрерывную в некоторой окрестности точки
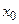
и имеющую конечную производную в этой точке. Возьмем на графике функции две точки:
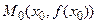
и
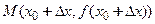
и проведем через них прямую
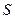
– секущую графика функции.

Эта прямая
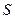
образует некоторый угол с положительным направлением оси
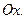
Проведем через точку
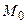
прямую, параллельную оси
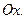
Точку пересечения этой прямой с вертикалью
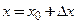
обозначим

Угол между секущей и осью
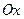
равен углу
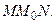
Очевидно, что для рассматриваемой возрастающей функции приращение функции
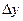
равно длине отрезка
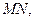
а приращение аргумента
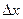
– длине отрезка
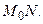
При 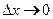 точка
точка  перемещается вдоль заданной кривой и неограниченно приближается к точке
перемещается вдоль заданной кривой и неограниченно приближается к точке  При этом секущая
При этом секущая 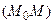 поворачивается вокруг точки
поворачивается вокруг точки 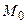 и стремится к предельному положению, называемому касательной к кривой в точке
и стремится к предельному положению, называемому касательной к кривой в точке  Эта прямая образует угол
Эта прямая образует угол 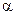 с положительным направлением оси абсцисс.
с положительным направлением оси абсцисс.
Угловой коэффициент секущей 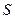 равен тангенсу угла
равен тангенсу угла 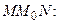
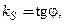 где
где 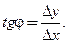 Угловой коэффициент касательной
Угловой коэффициент касательной 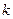 получим при помощи предельного перехода по формуле:
получим при помощи предельного перехода по формуле:
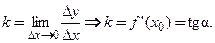 (3.6)
(3.6)
Отсюда следует геометрический смысл производной: значение производной 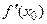 равно угловому коэффициенту касательной.
равно угловому коэффициенту касательной.
Касательная пересекает вертикаль  в точке
в точке  Абсцисса этой точки равна
Абсцисса этой точки равна 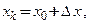 ордината
ордината 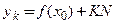 , где
, где 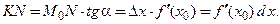 Так как производная
Так как производная 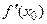 конечна, то и угловой коэффициент
конечна, то и угловой коэффициент  конечен и
конечен и  . Отсюда следует геометрический смысл дифференциала: значение дифференциала функции
. Отсюда следует геометрический смысл дифференциала: значение дифференциала функции  в точке
в точке 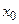 , соответствующего приращению аргумента
, соответствующего приращению аргумента 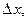 равноприращению ординаты касательной, проведенной к графику функции
равноприращению ординаты касательной, проведенной к графику функции 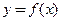 в точке
в точке 
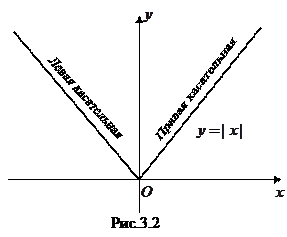
Если функция непрерывна в точке 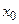 , не дифференцируема в этой точке, но имеет неравные конечные односторонние производные в этой точке, то через точку
, не дифференцируема в этой точке, но имеет неравные конечные односторонние производные в этой точке, то через точку 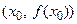 можно провести две односторонних касательных с угловыми коэффициентами, равными
можно провести две односторонних касательных с угловыми коэффициентами, равными 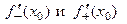 . Односторонние (левосторонняя и правосторонняя)касательные изображаются полупрямыми, ведущими с той или иной стороны (левой или правой) к точке
. Односторонние (левосторонняя и правосторонняя)касательные изображаются полупрямыми, ведущими с той или иной стороны (левой или правой) к точке 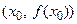 и имеющими указанные угловые коэффициенты.
и имеющими указанные угловые коэффициенты.
У функции  в точке
в точке 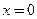 нет производной, но существуют односторонние производные
нет производной, но существуют односторонние производные  Ветви графика являются одновременно односторонними касательными к графику в начале координат (см. рис. 3.2).
Ветви графика являются одновременно односторонними касательными к графику в начале координат (см. рис. 3.2).
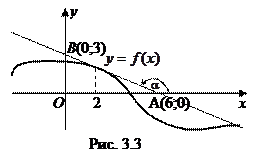 Пример 3.6. Найти значение производной
Пример 3.6. Найти значение производной 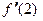 функции
функции 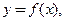 если касательная, проведенная к графику функции в точке
если касательная, проведенная к графику функции в точке  , пересекает координатные оси в точках
, пересекает координатные оси в точках 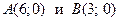 (см. рис. 3.3).
(см. рис. 3.3).
□ Значение 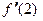 равно угловому коэффициенту
равно угловому коэффициенту 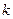 касательной. Касательная − прямая линия, проходящая через точки
касательной. Касательная − прямая линия, проходящая через точки  . По формуле (1.8) угловой коэффициент прямой, проходящей через две заданные точки
. По формуле (1.8) угловой коэффициент прямой, проходящей через две заданные точки  , равен
, равен 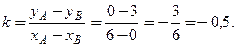 ■
■
Бесконечная производная. Рассмотрим функцию  , непрерывную на отрезке
, непрерывную на отрезке  и имеющую бесконечные производные в точках
и имеющую бесконечные производные в точках 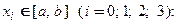
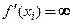 . В этом случае вертикальные прямые, уравнения которых
. В этом случае вертикальные прямые, уравнения которых  , являются касательными к графику функции
, являются касательными к графику функции  в точках
в точках 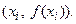
На рис. 3.4 приведены вертикальные касательные в этих точках, соответствующие следующим сочетаниям значений односторонних производных:
а) 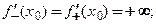 б)
б) 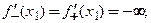 в)
в) 
г)

Подчеркнем, что во всех четырех случаях
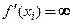
.
В примерах 3.4 и 3.5 рассмотрены функции с бесконечными производными в точке 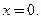 В обоих случаях через одну и ту же точку
В обоих случаях через одну и ту же точку  проходит вертикальная касательная, совпадаюшая с осью ординат. Принципиальное различие состоит в том, что одна функция −
проходит вертикальная касательная, совпадаюшая с осью ординат. Принципиальное различие состоит в том, что одна функция − 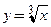 − непрерывна в точке
− непрерывна в точке 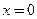 , а другая −
, а другая − 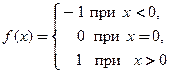 − терпит разрыв 1-го рода в точке
− терпит разрыв 1-го рода в точке 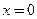 . На рис. 3.5 приведены графики обеих функций вместе с касательными, проходящими через точку
. На рис. 3.5 приведены графики обеих функций вместе с касательными, проходящими через точку 


 Таким образом, непрерывность функции в точке является необходимым условием существования только конечной производной. В случае бесконечной производной функция может быть как непрерывной, так и разрывной в соответствующей точке.
Таким образом, непрерывность функции в точке является необходимым условием существования только конечной производной. В случае бесконечной производной функция может быть как непрерывной, так и разрывной в соответствующей точке.
Механический смысл производной и дифференциала
Пусть 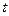 − время,
− время, 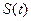 − путь, пройденный материальной точкой при прямолинейном движении за время
− путь, пройденный материальной точкой при прямолинейном движении за время 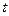 . Среднюю скорость движения
. Среднюю скорость движения  на временном отрезке
на временном отрезке 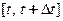 определяют так:
определяют так: 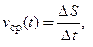 где
где 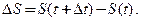 Скорость (мгновенную скорость) движения в момент времени
Скорость (мгновенную скорость) движения в момент времени 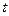 определяют при помощи операции предельного перехода:
определяют при помощи операции предельного перехода: 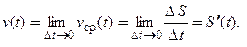 Значит, скорость движения
Значит, скорость движения 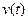 равна производной от пройденного пути
равна производной от пройденного пути 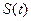 по времени t.
по времени t.
Дифференциал 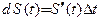 равен пути, пройденному с момента
равен пути, пройденному с момента 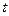 по момент времени
по момент времени 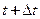 , при движении с постоянной скоростью, равной
, при движении с постоянной скоростью, равной 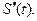
Пусть  − независимая переменная,
− независимая переменная, 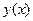 − некоторая функция, определенная на промежутке
− некоторая функция, определенная на промежутке 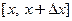 . По аналогии с задачей о движении точки средней скоростью изменения функции
. По аналогии с задачей о движении точки средней скоростью изменения функции 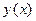 на отрезке
на отрезке 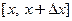 назовем
назовем 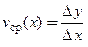 . Тогда скоростьизменения функции
. Тогда скоростьизменения функции 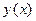 в точке
в точке  определяется при помощи операции предельного перехода
определяется при помощи операции предельного перехода 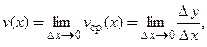 и равна значению производной функции
и равна значению производной функции 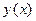 в точке
в точке  :
:  .
.
В механике при изучении прямолинейного движения точки наряду со скоростью используют понятие ускорения 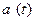 , которое определяют как скорость изменения скорости движения, т.е.
, которое определяют как скорость изменения скорости движения, т.е. 
Пример 3.5. Найти скорость прямолинейного движения точки, если зависимость пройденного пути от времени имеет вид: 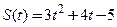 , при
, при 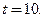
□ Искомая скорость  равна значению производной
равна значению производной  Производная
Производная 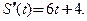 Эту соотношение можно вывести, используя определение производной или применяя правила дифференцирования, изложенные далее. Тогда
Эту соотношение можно вывести, используя определение производной или применяя правила дифференцирования, изложенные далее. Тогда 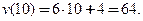 ■
■
Экономический смысл производной и дифференциала
В экономике производные применяют для получения предельных издержек производства или хранения, предельной выручки от продаж, предельной прибыли и т.п.
Если функция 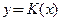 есть функция издержек (затрат) при производстве количества
есть функция издержек (затрат) при производстве количества  однородной продукции, то
однородной продукции, то 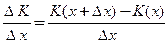 называют средним приращением издержек производства. Значение
называют средним приращением издержек производства. Значение 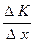 равно приращению издержек производства на единицу приращения количества продукции.
равно приращению издержек производства на единицу приращения количества продукции.
Производную 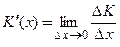 называют предельными издержками производства.
называют предельными издержками производства.
Аналогично, если 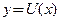 выручка от продажи
выручка от продажи 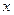 единиц товара, то производную
единиц товара, то производную 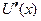 называют предельной выручкой.
называют предельной выручкой.
Если функция 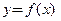 описывает зависимость цены некоторого товара (продукта) от времени
описывает зависимость цены некоторого товара (продукта) от времени 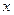 , то производная
, то производная 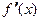 равна скорости изменения цены в выбранный момент времени
равна скорости изменения цены в выбранный момент времени  и ее называют тенденцией формирования цены товара.
и ее называют тенденцией формирования цены товара.
Дифференциал  функции издержек вычисляется по формуле:
функции издержек вычисляется по формуле:  . При
. При  получаем
получаем 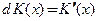 и по формуле (3.4) для приближенного вычисления приращения функции имеем
и по формуле (3.4) для приближенного вычисления приращения функции имеем 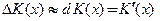 . Величине производной
. Величине производной 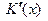 можно дать следующий экономический смысл: если произведено
можно дать следующий экономический смысл: если произведено  изделий, то дополнительные издержки
изделий, то дополнительные издержки 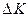 по производству
по производству 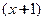 -го изделия приближенно равны предельным издержкам
-го изделия приближенно равны предельным издержкам 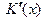 [21].
[21].
Пример 3.6. Издержки производства 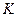 зависят от объема продукции по формуле
зависят от объема продукции по формуле 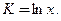 Определить предельные издержки, если объем продукции составляет 5 единиц. Найти дополнительные издержки по производству шестого изделия.
Определить предельные издержки, если объем продукции составляет 5 единиц. Найти дополнительные издержки по производству шестого изделия.
□ Имеем 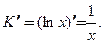 При
При  Дополнительные издержки по производству шестого изделия приближенно равны
Дополнительные издержки по производству шестого изделия приближенно равны 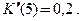 ■
■
Задачи для самостоятельного решения
1. Используя определения, найдите производные и дифференциалы следующих функций:

Ответы: 

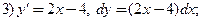
4) 
2. Определите значение производной 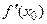 , если касательная, проведенная к графику функции
, если касательная, проведенная к графику функции 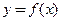 в точке
в точке 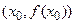 , пересекает координатные оси в точках
, пересекает координатные оси в точках  и
и  :
:
1) 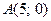 ,
, 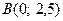 ; 2)
; 2) 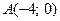
 ; 3)
; 3)  ,
,  ; 4)
; 4) 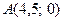 ,
, 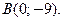
Ответы: 1) 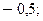 2)
2) 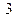 ; 3)
; 3) 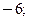 4)
4) 
3. К графику функции 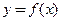 в точке
в точке 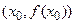 проведена касательная, проходящая через точки
проведена касательная, проходящая через точки 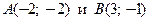 Определите значение производной
Определите значение производной 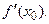
Ответ: 0,2.
4. К графику функции 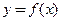 в точке
в точке 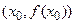 проведена касательная, которая образует с положительным направлением оси абсцисс угол: 1)
проведена касательная, которая образует с положительным направлением оси абсцисс угол: 1)  ; 2)
; 2)  ; 3)
; 3) 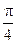 ; 4)
; 4) 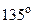 . Определите значение производной
. Определите значение производной 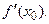
Ответы: 1) 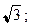 2)
2)  3)
3)  ; 4)
; 4) 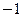 .
.
Табличное дифференцирование
Всякая элементарная функция в каждой точке области определения имеет производную, которая также является элементарной функцией. Выражения для производных основных элементарных функций приведены в табл. 3.1.
....................................... Таблица 3.1
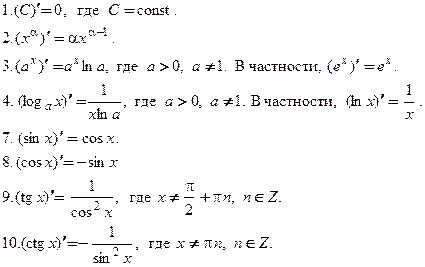
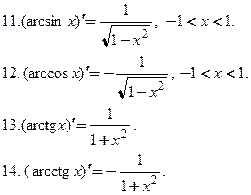
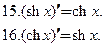

Формула Лейбница
Производную п- го порядка вычисляют путем последовательного п- кратного дифференцирования функции. Ниже приведены формулы для производных n -ого порядка некоторых элементарных функций:
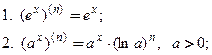
3. 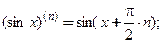
4. 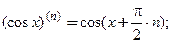
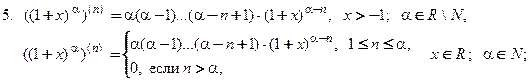
6. 
Правила вычисления производных высших порядков
1. Производная n-го порядка суммы или разности двух функций равна сумме или разности производных n-го порядка этих функций:

2. Формула Лейбница ( для п- й производной произведения). Производная n-го порядка произведения двух функций равна:
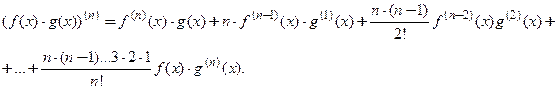 (3.17)
(3.17)
Вернемся к примеру 3.17. Вычислим третью производную 
|
|
|



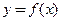 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки 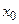 . Дадим аргументу
. Дадим аргументу  такое приращение
такое приращение 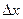 , что точка
, что точка 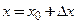 также принадлежит рассматриваемой окрестности. Соответствующее приращение функции
также принадлежит рассматриваемой окрестности. Соответствующее приращение функции 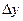 равно:
равно:  , или
, или 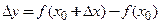 . Приращение функции
. Приращение функции  .
.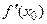 функции
функции  в точке
в точке  при стремлении последнего к нулю:
при стремлении последнего к нулю: 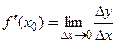 . (3.1)
. (3.1)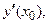

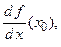
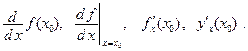 Производная может быть как конечной, так и бесконечной величиной. Если предел (3.1) не существует, то и производная
Производная может быть как конечной, так и бесконечной величиной. Если предел (3.1) не существует, то и производная 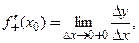
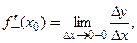
 и
и 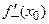 − правосторонняя (правая) и левосторонняя (левая) производная в точке
− правосторонняя (правая) и левосторонняя (левая) производная в точке 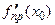 и
и  . В граничных точках отрезков можно определить только односторонние производные.
. В граничных точках отрезков можно определить только односторонние производные.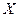 и ее производная существует при каждом значении
и ее производная существует при каждом значении 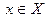 , то формула
, то формула 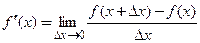 определяет производную как функцию аргумента
определяет производную как функцию аргумента 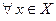 .
.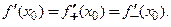
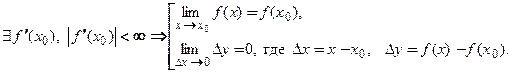
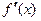 , если
, если  .
.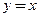 называют идентичной функцией.
называют идентичной функцией. , то
, то 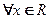 можно определить приращение функции
можно определить приращение функции 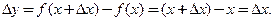
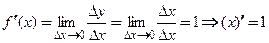 . ■
. ■ , если
, если 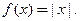
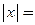
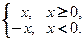
 и
и 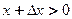
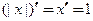 (см. пример 3.1).
(см. пример 3.1). и
и 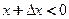 приращение функции равно:
приращение функции равно: 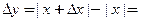
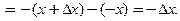 Отсюда, при
Отсюда, при  Тогда
Тогда 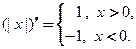
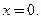 Найдем односторонние производные в этой точке:
Найдем односторонние производные в этой точке: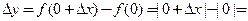
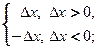
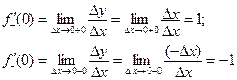
 не существует согласно теореме 3.1.
не существует согласно теореме 3.1.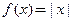 является примером функции, определенной и непрерывной на множестве
является примером функции, определенной и непрерывной на множестве  и имеющей производную на всей оси, кроме точки
и имеющей производную на всей оси, кроме точки 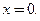 ■
■
 функции
функции  − это полуось
− это полуось  . Для
. Для 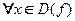 можно определить приращение функции
можно определить приращение функции 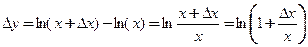 , если
, если Тогда согласно (3.1)
Тогда согласно (3.1) 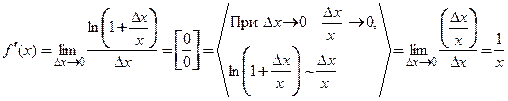 .
.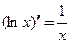
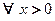 . ■
. ■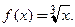
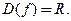 Для любого
Для любого 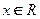 можно определить приращение функции
можно определить приращение функции 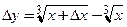 . Для удобства последующих вычислений преобразуем его:
. Для удобства последующих вычислений преобразуем его: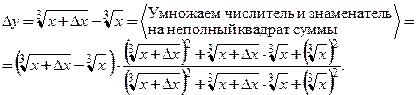
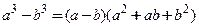 и получаем
и получаем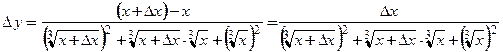 .
.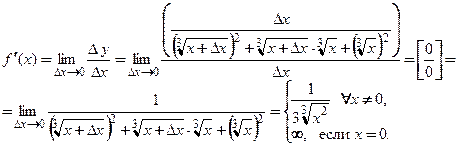
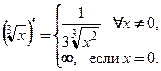
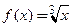 является примером функции определенной, непрерывной и имеющей производную на множестве
является примером функции определенной, непрерывной и имеющей производную на множестве 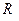 . Производная функции конечна во всех точках множества
. Производная функции конечна во всех точках множества 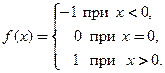
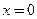 . В силу следствия из теоремы 3.2 в этой точке у функции нет конечной производной, так как точка
. В силу следствия из теоремы 3.2 в этой точке у функции нет конечной производной, так как точка 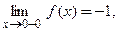
 и эти три числа не равны между собой.
и эти три числа не равны между собой. производная этой функции равна нулю:
производная этой функции равна нулю: 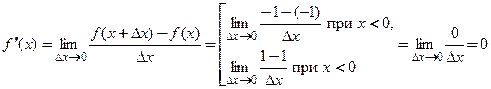 .
. :
: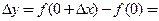
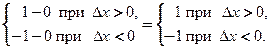


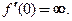 ■
■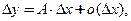 (3.2)
(3.2)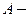 конечная величина, не зависящая от
конечная величина, не зависящая от 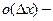 бесконечно малая величина высшего порядка малости относительно
бесконечно малая величина высшего порядка малости относительно 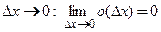 и
и 
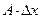 , называется дифференциалом функции и обозначается
, называется дифференциалом функции и обозначается 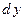 . Наряду с этим обозначением дифференциала используют и другие:
. Наряду с этим обозначением дифференциала используют и другие: 
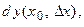
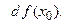
 (3.3)
(3.3)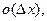 полагая его малой величиной, и приращение
полагая его малой величиной, и приращение 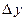 заменяют дифференциалом
заменяют дифференциалом 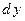 :
: (3.4)
(3.4) 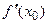 , при этом
, при этом , или кратко
, или кратко 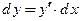 , (3.5)
, (3.5)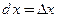 для независимой переменной
для независимой переменной 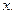
 является отношением дифференциалов
является отношением дифференциалов 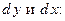
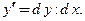 Значит, запись
Значит, запись  является не только обозначением производной, но и формулой для ее нахождения. Заметим, что теорема верна и для граничных точек отрезка, если под производной понимать одностороннюю производную.
является не только обозначением производной, но и формулой для ее нахождения. Заметим, что теорема верна и для граничных точек отрезка, если под производной понимать одностороннюю производную.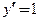 , т.е. производная существует и конечна при любых значениях
, т.е. производная существует и конечна при любых значениях  при любом
при любом 
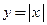 дифференцируема по теореме 3.3 при любых значениях
дифференцируема по теореме 3.3 при любых значениях 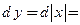
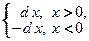 . При
. При 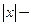 недифференцируемая функция, так как в этой точке производная не существует.
недифференцируемая функция, так как в этой точке производная не существует. дифференцируема по теореме 3.3 при любом положительном
дифференцируема по теореме 3.3 при любом положительном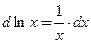 .
.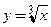 дифференцируема по теореме 3.3 при любых значениях
дифференцируема по теореме 3.3 при любых значениях 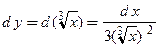 при
при 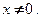 При
При 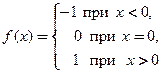 дифференцируема по теореме 3.3 при
дифференцируема по теореме 3.3 при  , при этом
, при этом 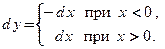 Функция
Функция 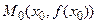 и
и 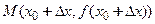 и проведем через них прямую
и проведем через них прямую 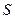 – секущую графика функции.
– секущую графика функции.

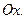 Проведем через точку
Проведем через точку 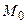 прямую, параллельную оси
прямую, параллельную оси  Угол между секущей и осью
Угол между секущей и осью 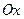 равен углу
равен углу 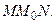 Очевидно, что для рассматриваемой возрастающей функции приращение функции
Очевидно, что для рассматриваемой возрастающей функции приращение функции 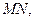 а приращение аргумента
а приращение аргумента 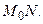
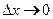 точка
точка  перемещается вдоль заданной кривой и неограниченно приближается к точке
перемещается вдоль заданной кривой и неограниченно приближается к точке  При этом секущая
При этом секущая 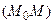 поворачивается вокруг точки
поворачивается вокруг точки 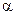 с положительным направлением оси абсцисс.
с положительным направлением оси абсцисс.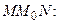
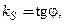 где
где 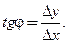 Угловой коэффициент касательной
Угловой коэффициент касательной 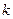 получим при помощи предельного перехода по формуле:
получим при помощи предельного перехода по формуле: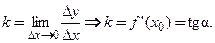 (3.6)
(3.6) в точке
в точке  Абсцисса этой точки равна
Абсцисса этой точки равна 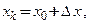 ордината
ордината 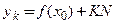 , где
, где 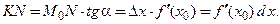 Так как производная
Так как производная  конечен и
конечен и  . Отсюда следует геометрический смысл дифференциала: значение дифференциала функции
. Отсюда следует геометрический смысл дифференциала: значение дифференциала функции 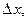 равноприращению ординаты касательной, проведенной к графику функции
равноприращению ординаты касательной, проведенной к графику функции 
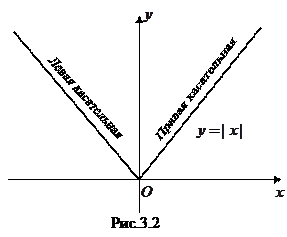
 можно провести две односторонних касательных с угловыми коэффициентами, равными
можно провести две односторонних касательных с угловыми коэффициентами, равными 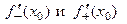 . Односторонние (левосторонняя и правосторонняя)касательные изображаются полупрямыми, ведущими с той или иной стороны (левой или правой) к точке
. Односторонние (левосторонняя и правосторонняя)касательные изображаются полупрямыми, ведущими с той или иной стороны (левой или правой) к точке  в точке
в точке  Ветви графика являются одновременно односторонними касательными к графику в начале координат (см. рис. 3.2).
Ветви графика являются одновременно односторонними касательными к графику в начале координат (см. рис. 3.2).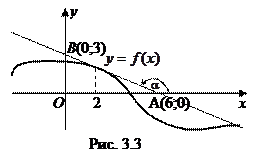 Пример 3.6. Найти значение производной
Пример 3.6. Найти значение производной 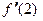 функции
функции 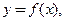 если касательная, проведенная к графику функции в точке
если касательная, проведенная к графику функции в точке  , пересекает координатные оси в точках
, пересекает координатные оси в точках 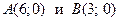 (см. рис. 3.3).
(см. рис. 3.3). . По формуле (1.8) угловой коэффициент прямой, проходящей через две заданные точки
. По формуле (1.8) угловой коэффициент прямой, проходящей через две заданные точки 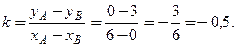 ■
■ и имеющую бесконечные производные в точках
и имеющую бесконечные производные в точках 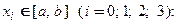
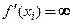 . В этом случае вертикальные прямые, уравнения которых
. В этом случае вертикальные прямые, уравнения которых  , являются касательными к графику функции
, являются касательными к графику функции  в точках
в точках 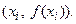
 б)
б) 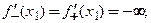 в)
в) 
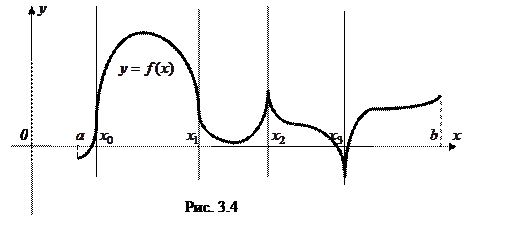
 Подчеркнем, что во всех четырех случаях
Подчеркнем, что во всех четырех случаях  проходит вертикальная касательная, совпадаюшая с осью ординат. Принципиальное различие состоит в том, что одна функция −
проходит вертикальная касательная, совпадаюшая с осью ординат. Принципиальное различие состоит в том, что одна функция − 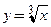 − непрерывна в точке
− непрерывна в точке 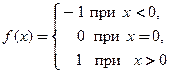 − терпит разрыв 1-го рода в точке
− терпит разрыв 1-го рода в точке 

 Таким образом, непрерывность функции в точке является необходимым условием существования только конечной производной. В случае бесконечной производной функция может быть как непрерывной, так и разрывной в соответствующей точке.
Таким образом, непрерывность функции в точке является необходимым условием существования только конечной производной. В случае бесконечной производной функция может быть как непрерывной, так и разрывной в соответствующей точке.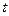 − время,
− время, 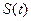 − путь, пройденный материальной точкой при прямолинейном движении за время
− путь, пройденный материальной точкой при прямолинейном движении за время  на временном отрезке
на временном отрезке 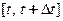 определяют так:
определяют так: 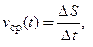 где
где 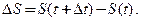 Скорость (мгновенную скорость) движения в момент времени
Скорость (мгновенную скорость) движения в момент времени 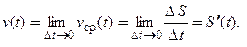 Значит, скорость движения
Значит, скорость движения 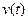 равна производной от пройденного пути
равна производной от пройденного пути 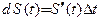 равен пути, пройденному с момента
равен пути, пройденному с момента 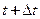 , при движении с постоянной скоростью, равной
, при движении с постоянной скоростью, равной 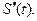
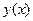 − некоторая функция, определенная на промежутке
− некоторая функция, определенная на промежутке 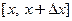 . По аналогии с задачей о движении точки средней скоростью изменения функции
. По аналогии с задачей о движении точки средней скоростью изменения функции 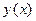 на отрезке
на отрезке 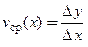 . Тогда скоростьизменения функции
. Тогда скоростьизменения функции 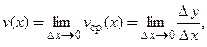 и равна значению производной функции
и равна значению производной функции  .
.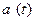 , которое определяют как скорость изменения скорости движения, т.е.
, которое определяют как скорость изменения скорости движения, т.е. 
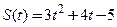 , при
, при 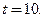
 равна значению производной
равна значению производной  Производная
Производная 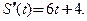 Эту соотношение можно вывести, используя определение производной или применяя правила дифференцирования, изложенные далее. Тогда
Эту соотношение можно вывести, используя определение производной или применяя правила дифференцирования, изложенные далее. Тогда 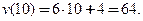 ■
■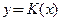 есть функция издержек (затрат) при производстве количества
есть функция издержек (затрат) при производстве количества 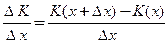 называют средним приращением издержек производства. Значение
называют средним приращением издержек производства. Значение 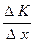 равно приращению издержек производства на единицу приращения количества продукции.
равно приращению издержек производства на единицу приращения количества продукции.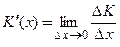 называют предельными издержками производства.
называют предельными издержками производства.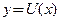 выручка от продажи
выручка от продажи 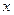 единиц товара, то производную
единиц товара, то производную 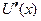 называют предельной выручкой.
называют предельной выручкой.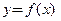 описывает зависимость цены некоторого товара (продукта) от времени
описывает зависимость цены некоторого товара (продукта) от времени 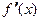 равна скорости изменения цены в выбранный момент времени
равна скорости изменения цены в выбранный момент времени  функции издержек вычисляется по формуле:
функции издержек вычисляется по формуле:  . При
. При  получаем
получаем 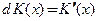 и по формуле (3.4) для приближенного вычисления приращения функции имеем
и по формуле (3.4) для приближенного вычисления приращения функции имеем 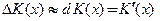 . Величине производной
. Величине производной 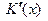 можно дать следующий экономический смысл: если произведено
можно дать следующий экономический смысл: если произведено 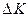 по производству
по производству 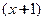 -го изделия приближенно равны предельным издержкам
-го изделия приближенно равны предельным издержкам 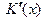 [21].
[21].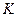 зависят от объема продукции по формуле
зависят от объема продукции по формуле 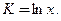 Определить предельные издержки, если объем продукции составляет 5 единиц. Найти дополнительные издержки по производству шестого изделия.
Определить предельные издержки, если объем продукции составляет 5 единиц. Найти дополнительные издержки по производству шестого изделия.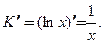 При
При  Дополнительные издержки по производству шестого изделия приближенно равны
Дополнительные издержки по производству шестого изделия приближенно равны 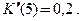 ■
■


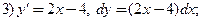

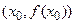 , пересекает координатные оси в точках
, пересекает координатные оси в точках  и
и  :
: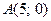 ,
, 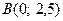 ; 2)
; 2) 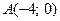
 ; 3)
; 3)  ,
,  ; 4)
; 4) 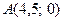 ,
, 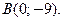
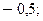 2)
2) 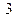 ; 3)
; 3) 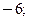 4)
4) 
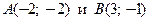 Определите значение производной
Определите значение производной 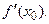
 ; 2)
; 2)  ; 3)
; 3) 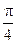 ; 4)
; 4) 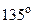 . Определите значение производной
. Определите значение производной 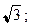 2)
2)  3)
3)  ; 4)
; 4) 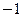 .
.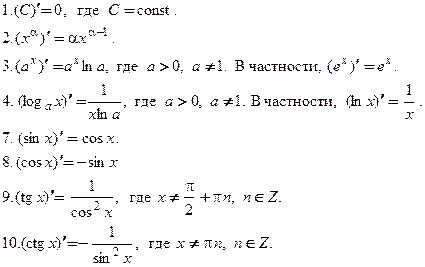
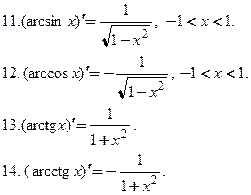
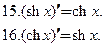

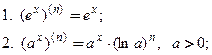
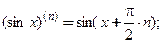
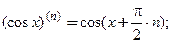
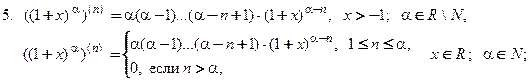


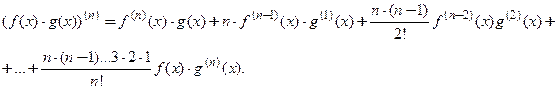 (3.17)
(3.17)


