Формула Лейбница
Производную п- го порядка вычисляют путем последовательного п- кратного дифференцирования функции. Ниже приведены формулы для производных n -ого порядка некоторых элементарных функций:
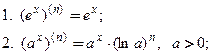
3. 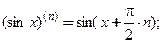
4. 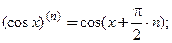
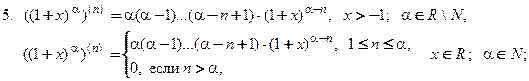
6. 
Правила вычисления производных высших порядков
1. Производная n-го порядка суммы или разности двух функций равна сумме или разности производных n-го порядка этих функций:

2. Формула Лейбница ( для п- й производной произведения). Производная n-го порядка произведения двух функций равна:
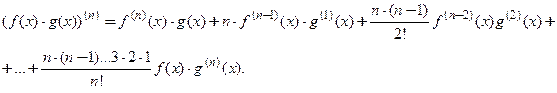 (3.17)
(3.17)
Вернемся к примеру 3.17. Вычислим третью производную 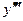 функции
функции 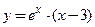 по формуле Лейбница, полагая
по формуле Лейбница, полагая 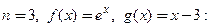
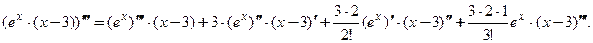
Производные любых порядков функции 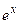 равны
равны 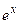 . Производные линейной функции
. Производные линейной функции 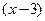 соответственно равны:
соответственно равны: 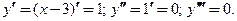 Производные подставляем в формулу Лейбница для третьей производной произведения и получаем прежний результат:
Производные подставляем в формулу Лейбница для третьей производной произведения и получаем прежний результат: 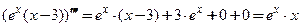 .
.
Пример 3.20. Показать, что функция 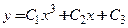 является решением дифференциального уравнения
является решением дифференциального уравнения 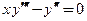 для
для 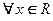 и произвольных значений постоянных
и произвольных значений постоянных 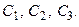
□ Найдем все производные заданной функции до 3-го порядка включительно: 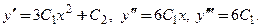 Подставим производные
Подставим производные 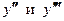 в дифференциальное уравнение:
в дифференциальное уравнение: 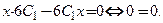 В итоге получим истинное равенство, выполненное при любых значениях
В итоге получим истинное равенство, выполненное при любых значениях 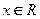 и произвольных значениях коэффициентов
и произвольных значениях коэффициентов 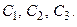 Вывод: функция
Вывод: функция 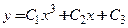 является решением заданного уравнения. ■
является решением заданного уравнения. ■
Параметрическое дифференцирование
Пусть функция 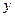 переменной
переменной 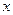 задана параметрическими уравнениями:
задана параметрическими уравнениями: 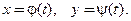 При наличии дифференцируемых производных функций
При наличии дифференцируемых производных функций 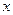 и
и 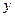 в некоторой точке
в некоторой точке 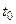 существуют соответствующие производные высших порядков функции
существуют соответствующие производные высших порядков функции 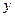 по
по 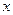 в этой точке, вычисляемые по формулам:
в этой точке, вычисляемые по формулам:
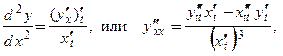 (3.16)
(3.16)
где 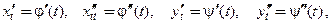
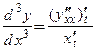 и так далее,
и так далее,
Пример 3.19. Найти 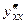 функции
функции 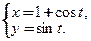
□ В примере 3.16 была найдена первая производная заданной функции: 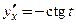 .
.
Применим формулу (3.16): 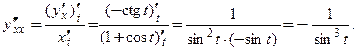 ■
■
Задачи для самостоятельного решения
1. Найдите производную 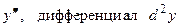 и их значения в точке
и их значения в точке 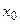 для следующих функций:
для следующих функций:
1) 
2) 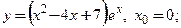
3) 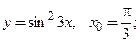
4) 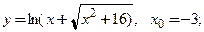
5) 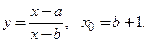
Ответы: 1) 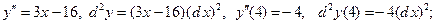
2) 
3) 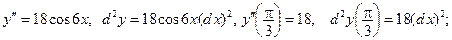
4) 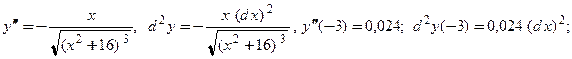
5) 
2. Найдите производные 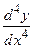 следующих функций:
следующих функций:
1) 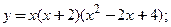 2)
2) 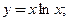 3)
3) 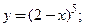 4)
4) 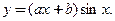
Ответы: 1) 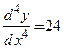 ; 2)
; 2) 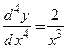 ; 3)
; 3) 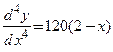 ; 4)
; 4) 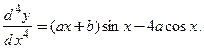
3. Выведите формулы для производных п- го порядка 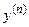 следующих функций:
следующих функций:
1) 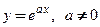 ; 2)
; 2) 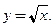
Ответы: 1) 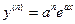 ; 2)
; 2) 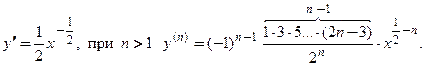
4. Найдите производные 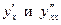 следующих функций:
следующих функций:
1)  2)
2) 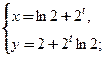 3)
3) 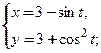 4)
4) 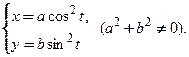
Ответы: 1) 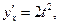
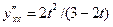 ; 2)
; 2) 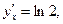
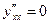 ; 3)
; 3) 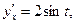
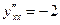 ;
;
4) 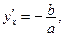
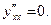
5. Покажите, что функция 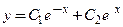 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 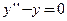 для
для 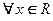 и произвольных значений постоянных
и произвольных значений постоянных 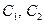 .
.
6. Покажите, что функция 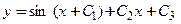 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 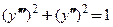 для
для 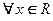 и произвольных значений постоянных
и произвольных значений постоянных  .
.
Основные теоремы дифференциального исчисления
Теоремы о среднем
Теорема 3.8 (Ферма). Если функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 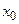 , принимает в этой точке наибольшее (наименьшее) значение и дифференцируема в ней, то в этой точке
, принимает в этой точке наибольшее (наименьшее) значение и дифференцируема в ней, то в этой точке 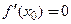 .
.
Эту теорему можно сформулировать по-иному, если ввести понятия точек максимума и минимума функции  .
.
Точка 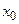 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если в некоторой окрестности этой точки выполняется неравенство
, если в некоторой окрестности этой точки выполняется неравенство 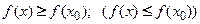 . Точки максимумов и минимумов называются точками экстремума. Понятие точек экстремума носит собирательный характер. Точки минимумов и максимумов также называют точками локального минимума или локального максимума в отличие от точек глобального минимума или максимума, в которых функция достигает своего наименьшего или наибольшего значения на некотором множестве
. Точки максимумов и минимумов называются точками экстремума. Понятие точек экстремума носит собирательный характер. Точки минимумов и максимумов также называют точками локального минимума или локального максимума в отличие от точек глобального минимума или максимума, в которых функция достигает своего наименьшего или наибольшего значения на некотором множестве 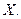 Значения функции в точках экстремума называют экстремумами − минимумом или максимумом соответственно.
Значения функции в точках экстремума называют экстремумами − минимумом или максимумом соответственно.
С учетом введенной терминологии теорему Ферма можно сформулировать более лаконично: в точках экстремума дифференцируемой функции производная обращается в нуль: 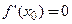 .
.
В теореме сформулировано необходимое условие экстремума дифференцируемой функции.
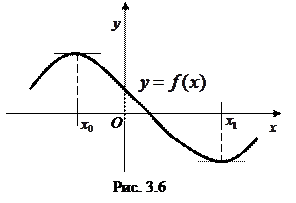 Эта теорема имеет наглядный геометрический смысл (см. рис. 3.6): в точках экстремума дифференцируемой функции касательная параллельна оси абсцисс.
Эта теорема имеет наглядный геометрический смысл (см. рис. 3.6): в точках экстремума дифференцируемой функции касательная параллельна оси абсцисс.
На графике функции  присутствуют две точки экстремума:
присутствуют две точки экстремума: 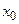 – точка максимума,
– точка максимума, 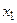 – точка минимума. В этих точках касательные параллельны оси
– точка минимума. В этих точках касательные параллельны оси 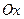 , так как их угловые коэффициенты равны нулю:
, так как их угловые коэффициенты равны нулю: 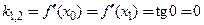 .
.
Теорема 3.9 (Ролля). Если функция  непрерывна на отрезке
непрерывна на отрезке 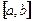 , дифференцируема на интервале
, дифференцируема на интервале 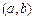 и на концах отрезка принимает равные значения
и на концах отрезка принимает равные значения 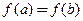 , то внутри интервала
, то внутри интервала 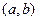 найдется, по крайней мере, одна такая точка
найдется, по крайней мере, одна такая точка 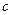 , что
, что 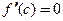 .
.
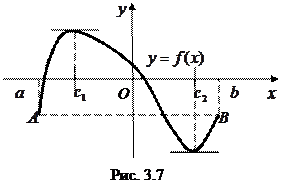 На рис. 3.7 приведен эскиз графика функции, удовлетворяющей всем условиям теоремы Ролля: 1.
На рис. 3.7 приведен эскиз графика функции, удовлетворяющей всем условиям теоремы Ролля: 1. 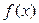 непрерывна на
непрерывна на 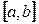 ;
;
2. 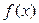 дифференцируема на
дифференцируема на 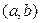 ;
;
3. 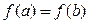 . В двух точках с абсциссами
. В двух точках с абсциссами 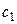 и
и 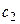 производная обращается в нуль. В этих точках касательная параллельна оси
производная обращается в нуль. В этих точках касательная параллельна оси 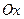 и параллельна хорде
и параллельна хорде 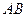 , «стягивающей концы» графика.
, «стягивающей концы» графика.
Теорема 3.10 (Коши). Если функции  и
и 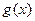 непрерывны на
непрерывны на 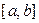 , дифференцируемы на
, дифференцируемы на 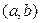 ,
, 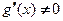 на
на 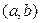 , то внутри интервала
, то внутри интервала 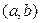 найдется, по крайней мере, одна такая точка
найдется, по крайней мере, одна такая точка 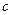 , что
, что
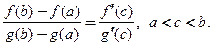 (3.18)
(3.18)
Эта формула носит название формулы Коши. Геометрического смысла не имеет, но применяется при доказательстве важных теорем.
Следствием теоремы Коши является теорема Лагранжа.
Теорема 3.11 (Лагранжа). Если функция  непрерывна на отрезке
непрерывна на отрезке 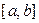 , дифференцируема на
, дифференцируема на 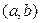 , то внутри интервала
, то внутри интервала 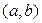 найдется, по крайней мере, одна такая точка
найдется, по крайней мере, одна такая точка 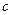 , что
, что
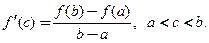 (3.19)
(3.19)
Из теоремы Лагранжа следует, что
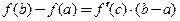 . (3.20)
. (3.20)
Соотношение (3.20) называют формулой конечных приращений. Если ввести обозначения: 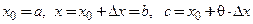 , где
, где 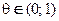 ,
, 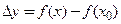 , то формулу конечных приращений можно переписать в виде:
, то формулу конечных приращений можно переписать в виде:
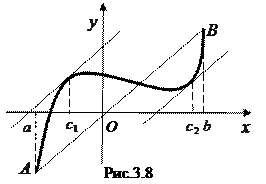
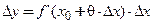 . (3.21)
. (3.21)
Геометрический смысл теоремы Лагранжа. Если функция  удовлетворяет условиям теоремы Лагранжа, то на графике функции найдется, по крайней мере, одна точка, в которой касательная параллельна хорде
удовлетворяет условиям теоремы Лагранжа, то на графике функции найдется, по крайней мере, одна точка, в которой касательная параллельна хорде 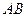 , «стягивающей концы» графика. На рис. (3.8) в двух точках графика с абсциссами
, «стягивающей концы» графика. На рис. (3.8) в двух точках графика с абсциссами 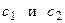 касательные параллельны хорде
касательные параллельны хорде 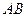 . Дробь
. Дробь 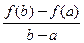 равна угловому коэффициенту секущей
равна угловому коэффициенту секущей 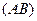 , что и объясняет приведенную формулу.
, что и объясняет приведенную формулу.
Формула Тейлора
Теорема 3.12 (Тейлора). Пусть функция  имеет конечную производную
имеет конечную производную 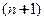 -го порядка в некоторой окрестности точки
-го порядка в некоторой окрестности точки 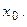 Тогда для любого
Тогда для любого 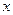 из этой окрестности найдется такая точка
из этой окрестности найдется такая точка 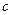 , расположенная между точками
, расположенная между точками 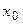 и
и 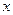 , что функция
, что функция  разлагается и притом единственным образом по степеням двучлена
разлагается и притом единственным образом по степеням двучлена 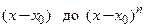 включительно по формуле:
включительно по формуле:
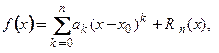 (3.22)
(3.22)
где 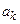 − коэффициенты Тейлора, определяемые соотношениями
− коэффициенты Тейлора, определяемые соотношениями
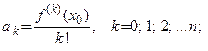 (3.23)
(3.23)
.
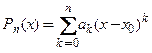 − многочлен Тейлора,
− многочлен Тейлора,
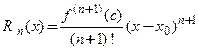 − остаточный член формулы Тейлора в форме Лагранжа.
− остаточный член формулы Тейлора в форме Лагранжа.
Формулу (3.22) называют формулой Тейлора 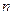 -го порядка. Она выражает функцию
-го порядка. Она выражает функцию  в виде суммы многочлена Тейлора п- ой степени по степеням
в виде суммы многочлена Тейлора п- ой степени по степеням 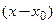 и остаточного члена. В развернутой записи формула Тейлора
и остаточного члена. В развернутой записи формула Тейлора 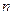 -го порядка с остаточным членом в форме Лагранжа имеет вид:
-го порядка с остаточным членом в форме Лагранжа имеет вид:
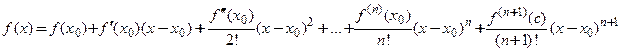 ,
,
или 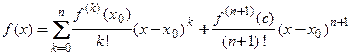 .
.
Известно много представлений остаточного члена 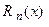 [Курант, Фихтенгольц]. Ограничимся описанием лишь двух из них. Одна форма − форма Лагранжа − приведена выше. Если промежуточную точку
[Курант, Фихтенгольц]. Ограничимся описанием лишь двух из них. Одна форма − форма Лагранжа − приведена выше. Если промежуточную точку 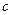 записать в виде
записать в виде 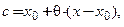 где число
где число 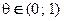 , то остаточный член в форме Лагранжа примет вид:
, то остаточный член в форме Лагранжа примет вид:
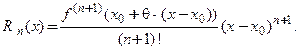
Если остаточный член записать в виде 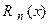
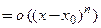 , то такую форму называют формой Пеано. При этом формула Тейлора с остаточным членом в форме Пеано запишется так:
, то такую форму называют формой Пеано. При этом формула Тейлора с остаточным членом в форме Пеано запишется так:
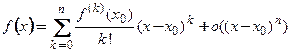 .
.
Здесь 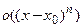 − бесконечно малая при
− бесконечно малая при 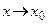 функция более высокого порядка малости, чем
функция более высокого порядка малости, чем 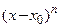 :
: 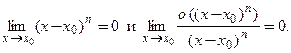
Абсолютная величина остаточного члена 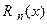 равна абсолютной погрешности при вычислении приближенного значения
равна абсолютной погрешности при вычислении приближенного значения  по формуле
по формуле 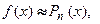 где
где 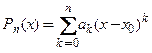 − многочлен Тейлора
− многочлен Тейлора 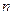 -й степени. Если функция
-й степени. Если функция  сама является многочленом
сама является многочленом 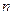 -й степени
-й степени 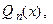 то приближенное равенство следует заменить на точное:
то приближенное равенство следует заменить на точное: 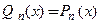 , так как в этом случае остаточный член в форме Лагранжа
, так как в этом случае остаточный член в форме Лагранжа 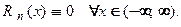
Если 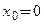 , то формулу (3.22) называют формулой Маклорена п-й степени.
, то формулу (3.22) называют формулой Маклорена п-й степени.
Формула Тейлора используется:
1) при переразложении многочлена, т.е. при преобразовании многочлена по степеням 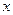 в многочлен по степеням
в многочлен по степеням 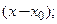
2) при приближенных выражениях элементарных функций с помощью многочленов;
3) для раскрытия неопределенностей при вычислении пределов;
4) в геометрии для изучения поведения графика функции в окрестности некоторой точки.
Пример 3.21. Переразложить многочлен 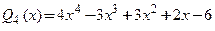 по степеням
по степеням 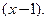
□ Воспользуемся формулой 3.22. В соответствии с условиями задачи примем 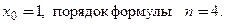 Разложение имеет вид
Разложение имеет вид 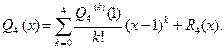 Сначала найдем все производные данного многочлена до 4-го порядка включительно и вычислим их значения в точке
Сначала найдем все производные данного многочлена до 4-го порядка включительно и вычислим их значения в точке 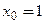 .
.
По формуле (3.23) найдем коэффициенты Тейлора:
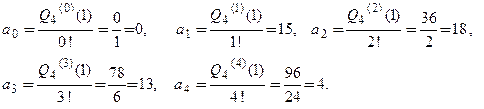
Производная 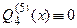 , поэтому
, поэтому 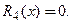 С учетом вычислений получим разложение:
С учетом вычислений получим разложение: 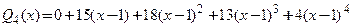 для любого
для любого 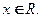
Заметим, что данный пример можно решить заменой  в многочлене
в многочлене 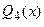 выражением
выражением 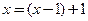 . Этот путь требует больших усилий и поэтому не рассматривается.■
. Этот путь требует больших усилий и поэтому не рассматривается.■
Пример 3.22. Разложить функцию 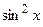 по степеням
по степеням 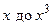 включительно.
включительно.
□ Здесь  Разложение по формуле Маклорена 3-го порядка с остаточным членом в форме Лагранжа имеет вид:
Разложение по формуле Маклорена 3-го порядка с остаточным членом в форме Лагранжа имеет вид:
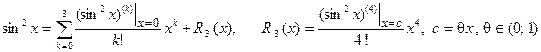 и применимо на всей числовой оси.
и применимо на всей числовой оси.
Найдем все производные данной функции до 4-го порядка включительно:
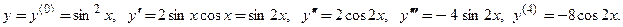
Далее: 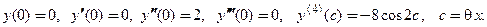
Искомое разложение 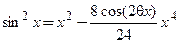 называется формулой Маклорена 3-го порядка для функции
называется формулой Маклорена 3-го порядка для функции 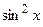 . ■
. ■


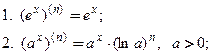
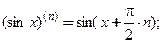
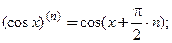
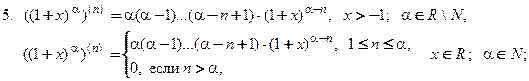


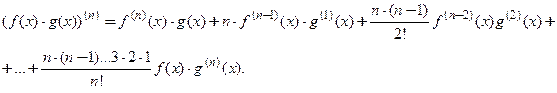 (3.17)
(3.17)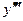 функции
функции 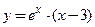 по формуле Лейбница, полагая
по формуле Лейбница, полагая 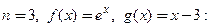
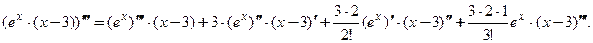
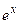 равны
равны 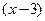 соответственно равны:
соответственно равны: 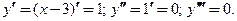 Производные подставляем в формулу Лейбница для третьей производной произведения и получаем прежний результат:
Производные подставляем в формулу Лейбница для третьей производной произведения и получаем прежний результат: 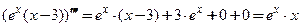 .
.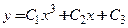 является решением дифференциального уравнения
является решением дифференциального уравнения 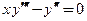 для
для 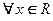 и произвольных значений постоянных
и произвольных значений постоянных 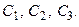
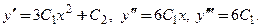 Подставим производные
Подставим производные 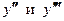 в дифференциальное уравнение:
в дифференциальное уравнение: 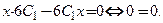 В итоге получим истинное равенство, выполненное при любых значениях
В итоге получим истинное равенство, выполненное при любых значениях 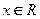 и произвольных значениях коэффициентов
и произвольных значениях коэффициентов  Вывод: функция
Вывод: функция 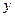 переменной
переменной 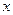 задана параметрическими уравнениями:
задана параметрическими уравнениями: 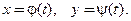 При наличии дифференцируемых производных функций
При наличии дифференцируемых производных функций 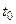 существуют соответствующие производные высших порядков функции
существуют соответствующие производные высших порядков функции 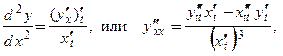 (3.16)
(3.16)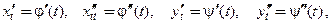
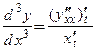 и так далее,
и так далее,  функции
функции 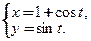
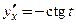 .
.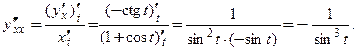 ■
■ и их значения в точке
и их значения в точке 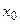 для следующих функций:
для следующих функций:
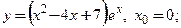
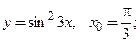
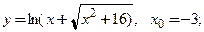
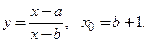
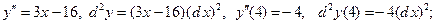

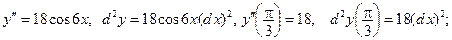
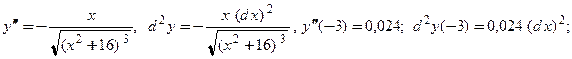

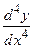 следующих функций:
следующих функций: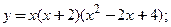 2)
2) 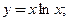 3)
3) 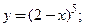 4)
4) 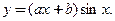
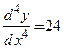 ; 2)
; 2) 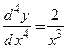 ; 3)
; 3) 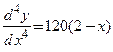 ; 4)
; 4) 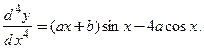
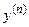 следующих функций:
следующих функций: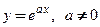 ; 2)
; 2) 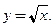
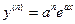 ; 2)
; 2) 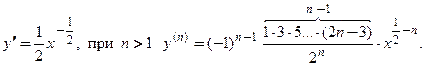
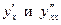 следующих функций:
следующих функций: 2)
2) 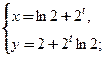 3)
3) 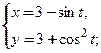 4)
4) 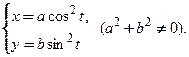
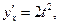
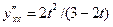 ; 2)
; 2) 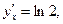
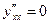 ; 3)
; 3) 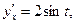
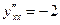 ;
; 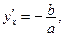
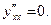
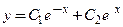 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 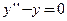 для
для 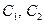 .
.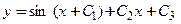 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 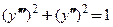 для
для  .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки 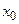 , принимает в этой точке наибольшее (наименьшее) значение и дифференцируема в ней, то в этой точке
, принимает в этой точке наибольшее (наименьшее) значение и дифференцируема в ней, то в этой точке 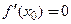 .
.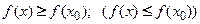 . Точки максимумов и минимумов называются точками экстремума. Понятие точек экстремума носит собирательный характер. Точки минимумов и максимумов также называют точками локального минимума или локального максимума в отличие от точек глобального минимума или максимума, в которых функция достигает своего наименьшего или наибольшего значения на некотором множестве
. Точки максимумов и минимумов называются точками экстремума. Понятие точек экстремума носит собирательный характер. Точки минимумов и максимумов также называют точками локального минимума или локального максимума в отличие от точек глобального минимума или максимума, в которых функция достигает своего наименьшего или наибольшего значения на некотором множестве 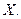 Значения функции в точках экстремума называют экстремумами − минимумом или максимумом соответственно.
Значения функции в точках экстремума называют экстремумами − минимумом или максимумом соответственно.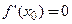 .
.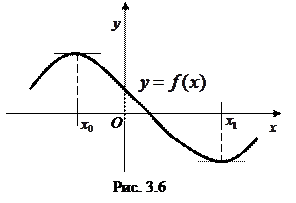 Эта теорема имеет наглядный геометрический смысл (см. рис. 3.6): в точках экстремума дифференцируемой функции касательная параллельна оси абсцисс.
Эта теорема имеет наглядный геометрический смысл (см. рис. 3.6): в точках экстремума дифференцируемой функции касательная параллельна оси абсцисс. – точка минимума. В этих точках касательные параллельны оси
– точка минимума. В этих точках касательные параллельны оси  , так как их угловые коэффициенты равны нулю:
, так как их угловые коэффициенты равны нулю: 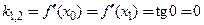 .
.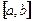 , дифференцируема на интервале
, дифференцируема на интервале 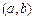 и на концах отрезка принимает равные значения
и на концах отрезка принимает равные значения 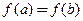 , то внутри интервала
, то внутри интервала 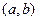 найдется, по крайней мере, одна такая точка
найдется, по крайней мере, одна такая точка 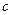 , что
, что 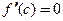 .
. 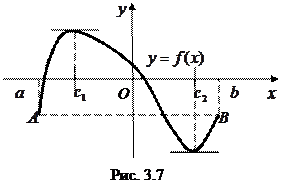 На рис. 3.7 приведен эскиз графика функции, удовлетворяющей всем условиям теоремы Ролля: 1.
На рис. 3.7 приведен эскиз графика функции, удовлетворяющей всем условиям теоремы Ролля: 1. 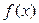 непрерывна на
непрерывна на 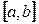 ;
;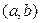 ;
;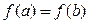 . В двух точках с абсциссами
. В двух точках с абсциссами 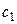 и
и 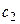 производная обращается в нуль. В этих точках касательная параллельна оси
производная обращается в нуль. В этих точках касательная параллельна оси 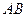 , «стягивающей концы» графика.
, «стягивающей концы» графика.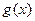 непрерывны на
непрерывны на 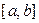 , дифференцируемы на
, дифференцируемы на 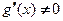 на
на 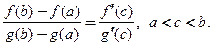 (3.18)
(3.18)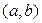 найдется, по крайней мере, одна такая точка
найдется, по крайней мере, одна такая точка 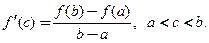 (3.19)
(3.19) 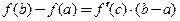 . (3.20)
. (3.20)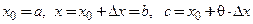 , где
, где 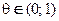 ,
, 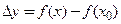 , то формулу конечных приращений можно переписать в виде:
, то формулу конечных приращений можно переписать в виде: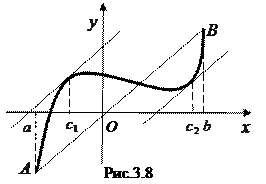
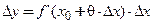 . (3.21)
. (3.21) , «стягивающей концы» графика. На рис. (3.8) в двух точках графика с абсциссами
, «стягивающей концы» графика. На рис. (3.8) в двух точках графика с абсциссами 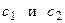 касательные параллельны хорде
касательные параллельны хорде 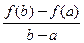 равна угловому коэффициенту секущей
равна угловому коэффициенту секущей  , что и объясняет приведенную формулу.
, что и объясняет приведенную формулу. -го порядка в некоторой окрестности точки
-го порядка в некоторой окрестности точки 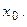 Тогда для любого
Тогда для любого 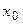 и
и 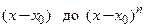 включительно по формуле:
включительно по формуле: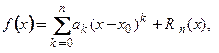 (3.22)
(3.22)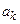 − коэффициенты Тейлора, определяемые соотношениями
− коэффициенты Тейлора, определяемые соотношениями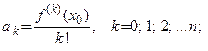 (3.23)
(3.23)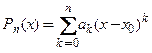 − многочлен Тейлора,
− многочлен Тейлора,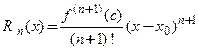 − остаточный член формулы Тейлора в форме Лагранжа.
− остаточный член формулы Тейлора в форме Лагранжа.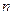 -го порядка. Она выражает функцию
-го порядка. Она выражает функцию 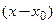 и остаточного члена. В развернутой записи формула Тейлора
и остаточного члена. В развернутой записи формула Тейлора 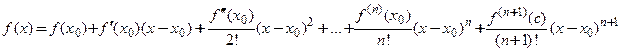 ,
,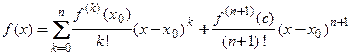 .
.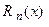 [Курант, Фихтенгольц]. Ограничимся описанием лишь двух из них. Одна форма − форма Лагранжа − приведена выше. Если промежуточную точку
[Курант, Фихтенгольц]. Ограничимся описанием лишь двух из них. Одна форма − форма Лагранжа − приведена выше. Если промежуточную точку 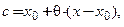 где число
где число 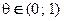 , то остаточный член в форме Лагранжа примет вид:
, то остаточный член в форме Лагранжа примет вид: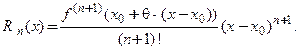
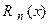
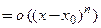 , то такую форму называют формой Пеано. При этом формула Тейлора с остаточным членом в форме Пеано запишется так:
, то такую форму называют формой Пеано. При этом формула Тейлора с остаточным членом в форме Пеано запишется так: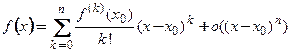 .
.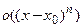 − бесконечно малая при
− бесконечно малая при 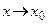 функция более высокого порядка малости, чем
функция более высокого порядка малости, чем 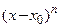 :
: 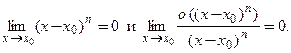
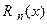 равна абсолютной погрешности при вычислении приближенного значения
равна абсолютной погрешности при вычислении приближенного значения 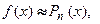 где
где 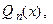 то приближенное равенство следует заменить на точное:
то приближенное равенство следует заменить на точное: 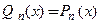 , так как в этом случае остаточный член в форме Лагранжа
, так как в этом случае остаточный член в форме Лагранжа 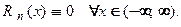
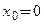 , то формулу (3.22) называют формулой Маклорена п-й степени.
, то формулу (3.22) называют формулой Маклорена п-й степени.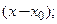
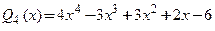 по степеням
по степеням 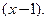
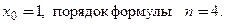 Разложение имеет вид
Разложение имеет вид 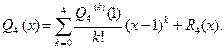 Сначала найдем все производные данного многочлена до 4-го порядка включительно и вычислим их значения в точке
Сначала найдем все производные данного многочлена до 4-го порядка включительно и вычислим их значения в точке 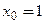 .
.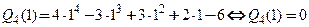 ;
;
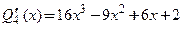 ,
,
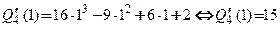 ;
;
 ,
,
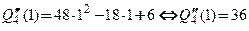 ;
;
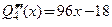 ,
,
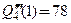 ;
;
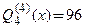 ,
,
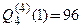 .
.
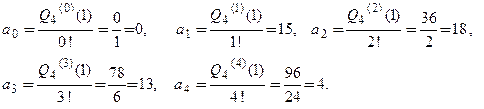
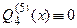 , поэтому
, поэтому 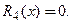 С учетом вычислений получим разложение:
С учетом вычислений получим разложение: 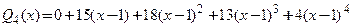 для любого
для любого 
 выражением
выражением 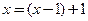 . Этот путь требует больших усилий и поэтому не рассматривается.■
. Этот путь требует больших усилий и поэтому не рассматривается.■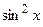 по степеням
по степеням 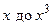 включительно.
включительно. Разложение по формуле Маклорена 3-го порядка с остаточным членом в форме Лагранжа имеет вид:
Разложение по формуле Маклорена 3-го порядка с остаточным членом в форме Лагранжа имеет вид: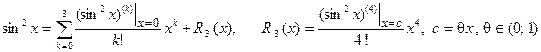 и применимо на всей числовой оси.
и применимо на всей числовой оси.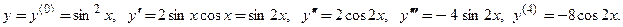
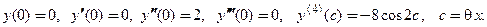
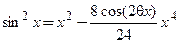 называется формулой Маклорена 3-го порядка для функции
называется формулой Маклорена 3-го порядка для функции