В параграфе 1.2. рассматривалась модель динамики мультипликатора с учетом внешней торговли, в которой экспорт предполагался экзогенным. В действительности экспорт косвенно зависит от национального дохода. Предположим, к примеру, что в стране (назовем ее «страна 1») происходит изменение дохода. Затем также изменяется объем импорта, который зависит от дохода, и это изменение означает изменение экспорта в «страну 1» для всего остального мира (для простоты будем считать для другой страны, назовем ее «страна 2»). Изменение объема экспорта в «стране 2» приводит к изменению дохода, что в свою очередь изменяет объем импорта «страны 2» из «страны 1». Это приводит к изменению объемов экспорта «страны 1», и так далее.
Эта цепочка событий известна под названием «внешнеторговая отдача» (foreign repercussion) и мультипликатор, который ее учитывает, называется мультипликатором с внешнеторговой отдачей. Для терминологического удобства мультипликатор, рассмотренный в 1.2., будем называть «мультипликатором внешней торговли без отдачи».
Начнем со статической модели, которая состоит из следующих уравнений:
Страна 1 Страна 2
 ,
,  ,
,
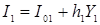 ,
, 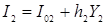 ,
,
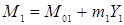 ,
,  ,
,
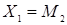 ,
, 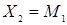 ,
,
 .
.  .
.
Эти уравнения выражают соответственно функции потребления, функции инвестирования, функции импорта, тот факт, что экспорт одной страны совпадает с импортом другой страны, и определение для национального дохода в условиях открытой экономики.  и
и  – автономные компоненты. Индексы 1 и 2 соответственно отображают состояние «страны 1» и «страны 2».
– автономные компоненты. Индексы 1 и 2 соответственно отображают состояние «страны 1» и «страны 2».
Делая подстановки первых четырех уравнений в пятое для обоих стран, получаем:
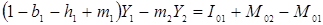 , (5.7)
, (5.7)
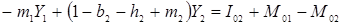 .
.
Откуда
 , (5.8)
, (5.8)
 ,
,
и, учитывая преобразования, получим:
 , (5.9)
, (5.9)
 .
.
Рассмотрим полученные выражения в динамическом аспекте. Предположения относительно модели те же, что и в 2.2., то есть в обоих странах  ,
,  и
и 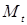 зависят от
зависят от  . После обычных подстановок получаем систему разностных уравнений
. После обычных подстановок получаем систему разностных уравнений
 , (5.10)
, (5.10)
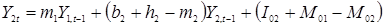 .
.
Частное решение системы (5.10) получают в виде 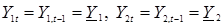 , где
, где  ,
,  – постоянные; величины, которые мы получили полностью совпадают со статическими точками равновесия (5.8).
– постоянные; величины, которые мы получили полностью совпадают со статическими точками равновесия (5.8).
Характеристическое уравнение для однородной формы системы (5.10):
 . (5.11)
. (5.11)
Теперь, поскольку  (см. 2.2.), коэффициенты положительны. Применим условия стабильности. Необходимыми и достаточными условиями стабильности являются:
(см. 2.2.), коэффициенты положительны. Применим условия стабильности. Необходимыми и достаточными условиями стабильности являются:
 , (5.12)
, (5.12)
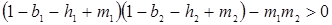 .
.
Если необходимы только достаточные условия, то получим
 , (5.13)
, (5.13)
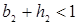 .
.
Из (5.12) и (5.13) можно сделать следующие выводы:
1. Необходимое (но не достаточное) условие стабильности заключается в том, что  и
и 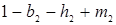 оба должны быть положительны.
оба должны быть положительны.
2. Достаточное (но не необходимое) условие стабильности 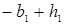 и
и  должны быть меньше 1.
должны быть меньше 1.
3. Если  , а также
, а также  , то модель нестабильна.
, то модель нестабильна.
4. Если одна из величин  ,
,  больше единицы, а другая меньше, то модель может проявлять как стабильное, так и нестабильное поведение в зависимости от соотношения
больше единицы, а другая меньше, то модель может проявлять как стабильное, так и нестабильное поведение в зависимости от соотношения 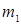 и
и 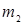 .
.
Чтобы оценить экономический смысл этих выводов, следует вспомнить из 2.2., что 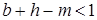 – это условие стабильности для мультипликатора внешней торговли без отдачи, а
– это условие стабильности для мультипликатора внешней торговли без отдачи, а 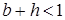 – это условие стабильности для мультипликатора закрытой экономики. Таким образом, можно сделать следующие выводы:
– это условие стабильности для мультипликатора закрытой экономики. Таким образом, можно сделать следующие выводы:
1. Необходимое (но не достаточное) условие стабильности для мультипликатора внешней торговли с внешнеторговой отдачей является то, что мультипликаторы обоих стран без внешнеторговой отдачи стабильны.
2. Достаточным (но не необходимым) условием стабильности мультипликатора с внешнеторговой отдачей является то, что для обоих изолированных стран мультипликатор закрытой экономики стабилен.
3. Если для обоих изолированных стран мультипликатор закрытой экономики нестабилен, то мультипликатор внешней торговли с отдачей также нестабилен.
4. Если, в предположении, что каждая страна предполагается изолированной, окажется, что в одной из них мультипликатор закрытой экономики стабилен, в то время как в другой – нет, то мультипликатор внешней торговли с отдачей может быть стабилен или нестабилен.
Модель мультипликатора с внешнеторговой отдачей может быть легко распространена на случай с несколькими странами. Пусть  – (частичная) склонность страны
– (частичная) склонность страны  к импорту из страны
к импорту из страны  , тогда
, тогда

является общей склонностью к импорту страны  . Аналогично:
. Аналогично:
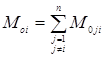 ,
,
где  – автономный импорт страны
– автономный импорт страны  из страны
из страны  . Тогда для любой страны
. Тогда для любой страны 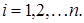 :
:


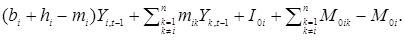 (5.14)
(5.14)
Характеристическое уравнение для однородной части системы (5.14):
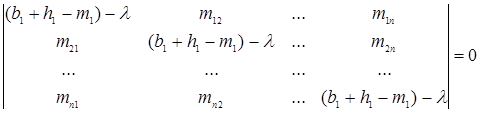 .
.
Применив условия стабильности, можно сделать выводы схожие с теми, которые были получены для случая с двумя странами. К примеру,  для всех
для всех 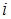 – это достаточное условие стабильности, в то время как при
– это достаточное условие стабильности, в то время как при  модель становится нестабильной. Более того, необходимое и достаточное условия стабильности также гарантируют, что статическое равновесие для неоднородной системы существует и имеет экономический смысл. Частное решение системы (5.14) –
модель становится нестабильной. Более того, необходимое и достаточное условия стабильности также гарантируют, что статическое равновесие для неоднородной системы существует и имеет экономический смысл. Частное решение системы (5.14) –  , где
, где 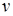 – вектор-столбец независимых (автономных) величин, а матрица A – матрица коэффициентов (очевидно положительных) дифференциальной системы. Известно, что положительность ведущих главных миноров матрицы
– вектор-столбец независимых (автономных) величин, а матрица A – матрица коэффициентов (очевидно положительных) дифференциальной системы. Известно, что положительность ведущих главных миноров матрицы  обеспечивает то, что
обеспечивает то, что  неотрицательна.
неотрицательна.





 ,
,  ,
,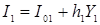 ,
, 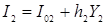 ,
,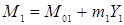 ,
,  ,
,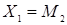 ,
, 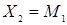 ,
, .
.  .
. и
и  – автономные компоненты. Индексы 1 и 2 соответственно отображают состояние «страны 1» и «страны 2».
– автономные компоненты. Индексы 1 и 2 соответственно отображают состояние «страны 1» и «страны 2».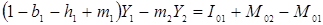 , (5.7)
, (5.7)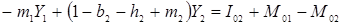 .
. , (5.8)
, (5.8) ,
, , (5.9)
, (5.9) .
. ,
,  и
и 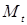 зависят от
зависят от  . После обычных подстановок получаем систему разностных уравнений
. После обычных подстановок получаем систему разностных уравнений , (5.10)
, (5.10)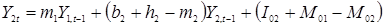 .
.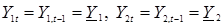 , где
, где  ,
,  – постоянные; величины, которые мы получили полностью совпадают со статическими точками равновесия (5.8).
– постоянные; величины, которые мы получили полностью совпадают со статическими точками равновесия (5.8). . (5.11)
. (5.11) (см. 2.2.), коэффициенты положительны. Применим условия стабильности. Необходимыми и достаточными условиями стабильности являются:
(см. 2.2.), коэффициенты положительны. Применим условия стабильности. Необходимыми и достаточными условиями стабильности являются: , (5.12)
, (5.12)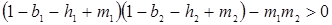 .
. , (5.13)
, (5.13)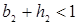 .
. и
и 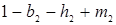 оба должны быть положительны.
оба должны быть положительны.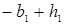 и
и  должны быть меньше 1.
должны быть меньше 1. , а также
, а также  , то модель нестабильна.
, то модель нестабильна. ,
,  больше единицы, а другая меньше, то модель может проявлять как стабильное, так и нестабильное поведение в зависимости от соотношения
больше единицы, а другая меньше, то модель может проявлять как стабильное, так и нестабильное поведение в зависимости от соотношения 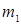 и
и 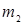 .
.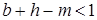 – это условие стабильности для мультипликатора внешней торговли без отдачи, а
– это условие стабильности для мультипликатора внешней торговли без отдачи, а 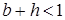 – это условие стабильности для мультипликатора закрытой экономики. Таким образом, можно сделать следующие выводы:
– это условие стабильности для мультипликатора закрытой экономики. Таким образом, можно сделать следующие выводы: – (частичная) склонность страны
– (частичная) склонность страны  к импорту из страны
к импорту из страны  , тогда
, тогда
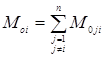 ,
, – автономный импорт страны
– автономный импорт страны  из страны
из страны  . Тогда для любой страны
. Тогда для любой страны 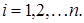 :
:

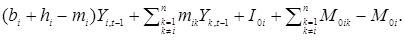 (5.14)
(5.14)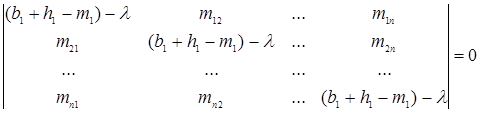 .
. для всех
для всех 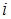 – это достаточное условие стабильности, в то время как при
– это достаточное условие стабильности, в то время как при  , где
, где 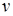 – вектор-столбец независимых (автономных) величин, а матрица A – матрица коэффициентов (очевидно положительных) дифференциальной системы. Известно, что положительность ведущих главных миноров матрицы
– вектор-столбец независимых (автономных) величин, а матрица A – матрица коэффициентов (очевидно положительных) дифференциальной системы. Известно, что положительность ведущих главных миноров матрицы  обеспечивает то, что
обеспечивает то, что  неотрицательна.
неотрицательна.


