Наиболее простой иллюстрацией вышеизложенным положениям служит паутинообразная модель рыночного равновесия, которая является одной из классических экономико-математических моделей. Эта динамическая модель была получена из статической модели спроса и предложения. Предположим, что предложение 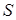 реагирует на изменение цены
реагирует на изменение цены 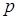 с лагом в один период, в то время как спрос
с лагом в один период, в то время как спрос 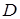 определяется ценой, и обе эти зависимости линейны:
определяется ценой, и обе эти зависимости линейны:
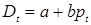 ,
,
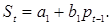
Почему предложение ведет себя таким образом? Во-первых, модель относится к продукции, которая не производится мгновенно – требуется фиксированный промежуток времени (совпадающий по величине с дискретом времени). Решающим ограничением является то, что производители считают, что цена, установленная в начале периода, не изменяется на его протяжении и является основой для выбора объемов производства в будущем периоде.
Существенным предположением модели является очистка рынка. В каждом периоде рынок устанавливает такую цену, при которой спрос поглощает в точности весь объем предложения, то есть нет поставщиков с нераспроданным товаром и потребителей с неудовлетворенным спросом. То есть формально:
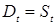 ,
,
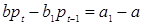 . (1.1)
. (1.1)
Общее решение соответствующего однородного уравнения равно 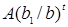 , а частное решение (1.1):
, а частное решение (1.1):
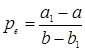 .
.
В предположении, что 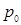 известно,
известно, 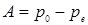 .
.
Общее решение (1.1) в этом случае равняется
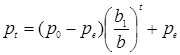 . (1.2)
. (1.2)
В этом случае частное решение получает экономическую интерпретацию статической цены равновесия. Из (1.2) видно, что, если начальное значение цены 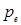 установлено, то
установлено, то 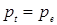 , то есть цена фиксируется на уровне
, то есть цена фиксируется на уровне 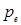 (естественно, при условии, что никакие экзогенные возмущения не возникают). Это и означает, что наблюдается статическое равновесие. Другой способ проверить это утверждение - проанализировать поведение цены во времени в соответствии с уравнением (1.2).
(естественно, при условии, что никакие экзогенные возмущения не возникают). Это и означает, что наблюдается статическое равновесие. Другой способ проверить это утверждение - проанализировать поведение цены во времени в соответствии с уравнением (1.2).
Обычно, график спроса имеет отрицательный угол наклона 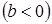 , а предложение - положительный
, а предложение - положительный 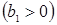 . Таким образом,
. Таким образом, 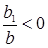 , и цена будет производить колебательные движения вокруг своего равновесного значения. Эти периодические колебания могут осуществляться с увеличивающимся, постоянным или уменьшающимся периодом (рис. 1.3.), в зависимости от соотношения
, и цена будет производить колебательные движения вокруг своего равновесного значения. Эти периодические колебания могут осуществляться с увеличивающимся, постоянным или уменьшающимся периодом (рис. 1.3.), в зависимости от соотношения 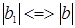 | (символ
| (символ 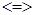 означает «меньше, равно или больше»), то есть в зависимости от того, превосходит ли угол наклона кривой спроса, угол наклона кривой предложения.
означает «меньше, равно или больше»), то есть в зависимости от того, превосходит ли угол наклона кривой спроса, угол наклона кривой предложения.
Как видно из (1.2), условие стабильности, то есть условие при котором цена сходится - не важно каким образом - к равновесному значению, в любом случае 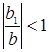 , то есть
, то есть 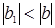 .
.
Теорема 1.1. (теорема о рыночном равновесии в паутинообразной модели) В паутинообразной модели точка равновесия является стабильной, если угол наклона кривой спроса больше чем угол наклона кривой предложения.
Эта теорема описывает лишь стабильность классической паутинообразной модели, но не гарантирует того, что для модели, содержащей некоторые дополнительные условия, условия стабильности останутся теми же.
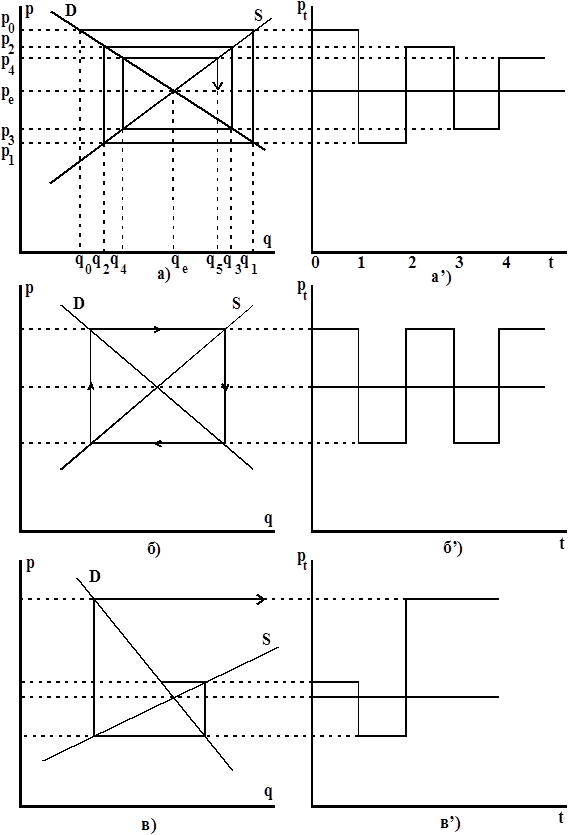
Рисунок 1.3. Теорема о рыночном равновесии в паутинообразной модели.
Нормальная цена
Рассуждения, опирающиеся на предположения о неизменности уровня рыночных цен, используемые при планировании объемов продаж, на практике оказываются, как правило, неприменимыми. Известный экономист Маршалл предложил методику, которая позволяла в какой-то мере избавиться от этого губительного предположения на этапе планирования.
Воспользуемся методикой Маршалла и покажем, что ее использование оказывает на модель в целом стабилизирующее воздействие. Традиционная паутинообразная модель рыночного равновесия может быть представлена как частный случай более общей модели:
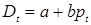 ,
,
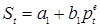 , (1.3)
, (1.3)
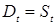 ,
,
где 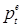 - цена, ожидаемая производителями, то есть цена, которая установится, по их мнению, на момент реализации продукции. Теорема о рыночном равновесии предполагает в качестве основного допущения, что
- цена, ожидаемая производителями, то есть цена, которая установится, по их мнению, на момент реализации продукции. Теорема о рыночном равновесии предполагает в качестве основного допущения, что 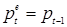 .
.
Таким образом, кажется неразумным предполагать, что производители будут ожидать, что цена останется на своем предыдущем уровне, в то время как она напротив варьируется от периода к периоду. Все учатся на опыте. Поэтому в модель следует ввести некоторые дополнения и усовершенствования.
Под нормальной ценой 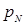 понимается цена, которая, по мнению производителя, рано или поздно установится на рынке. Поэтому, если текущая цена отличается от нормальной, они считают, что смогут изменить ее в дальнейшем. Другими словами
понимается цена, которая, по мнению производителя, рано или поздно установится на рынке. Поэтому, если текущая цена отличается от нормальной, они считают, что смогут изменить ее в дальнейшем. Другими словами
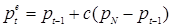 ,
, 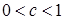 . (1.4)
. (1.4)
Следует отметить, что отдельный вопрос представляет собой определение значения нормальной цены. Идеальным вариантом было бы установить ее на уровне цены статического равновесия, однако в условиях отсутствия полной информации подобный подход оказывается неприменимым. Пусть 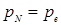 , и
, и
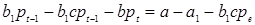 , (1.5)
, (1.5)
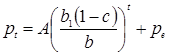 . (1.6)
. (1.6)
Условие стабильности:
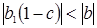 . (1.7)
. (1.7)
На рисунке 1.4 представлены некоторые нестандартные ситуации, которые относятся к случаям, когда кривые спроса и предложения имеют наклон в одну сторону. Отметим, что даже в этом случае имеют место стабильность и нестабильность равновесия.
Выражение 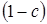 в 1.7 положительно и меньше единицы, так как
в 1.7 положительно и меньше единицы, так как 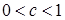 . Значит абсолютное значение
. Значит абсолютное значение 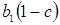 меньше, чем абсолютное значение
меньше, чем абсолютное значение 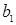 . Сравнив с первоначальной теоремой о рыночном равновесии, получим следующие результаты:
. Сравнив с первоначальной теоремой о рыночном равновесии, получим следующие результаты:
1) Сходимость сохраняется, ее темп увеличивается
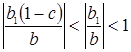 ,
,
модуль 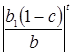 стремится к нулю быстрее, чем модуль
стремится к нулю быстрее, чем модуль 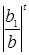 .
.
2) Периодические колебания с постоянной амплитудой становятся затухающими, так как, если 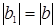 , то
, то
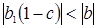 .
.
3) Расходимость может смениться сходимостью, если параметр с существенно близок к единице, так как вполне вероятно, что
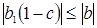 , даже при
, даже при 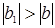 .
.
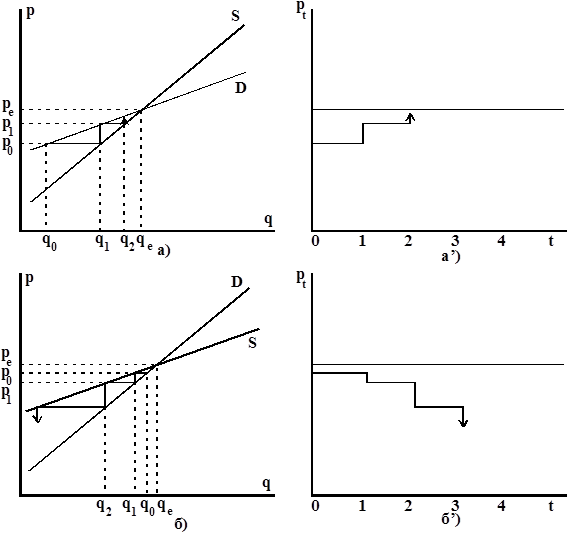
Рисунок 1.4. Нестандартные ситуации
Полученные результаты показывают, что введение в модель нормальной цены делает ее поведение более стабильной.
Адаптивные ожидания
Другой способ совершенствования паутинообразной модели рыночного равновесия - использование адаптивных ожиданий. Планы, которые принимаются в каждый данный период, зависят не только от текущих цен, но и от ожиданий будущих цен. Эти ожидания мы будем толковать, как правило, однозначно и жестко, полагая, что у каждого индивида складываются определенные представления о том, какой будет, по его мнению, цена того или иного интересующего его товара в том или ином периоде. Разумеется, такое предположение чрезмерно жестко. Оно, в действительности, неправомерно по двум причинам.
При необходимости, обсуждая все эти проблемы, связанные с факторами, определяющими планы, допустить неопределенность ожиданий мы должны считать самое вероятное значение цены не репрезентативной ожидаемой ценой, а суммой наиболее вероятных цен ± поправка на неопределенность ожиданий (или, иначе говоря, поправка на риск):
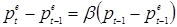 , (1.8)
, (1.8)
где 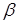 - положительный коэффициент меньше единицы.
- положительный коэффициент меньше единицы.
Таким образом, предположим формально, что люди ожидают установления тех или иных точных цен, то есть что у них формируются определенные ценовые ожидания. Но будем готовыми к тому, чтобы интерпретировать эти определенные ожидания как особые величины, которые наилучшим образом отражают условия неопределенности действительных ожиданий.
Запишем разностное уравнение:
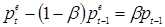 (1.9)
(1.9)
Отметим, что общее решение соответствующего однородного уравнения:
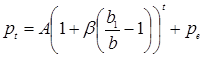 . (1.10)
. (1.10)
Соответствующее частное решение:
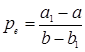 . (1.11)
. (1.11)
Общее решение (1.9):
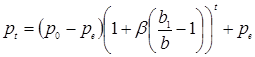 . (1.12)
. (1.12)
Это означает, что ожидаемая цена представляет собой средневзвешенную величину с убывающими во времени весами всех наблюдавшихся цен.
Так как
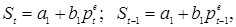
откуда
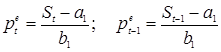 .
.
Подставляя эти значения в (1.9) получим:
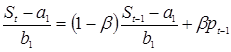 ,
,
откуда
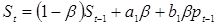 . (1.13)
. (1.13)
Поскольку 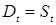 для всех
для всех 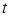 по условию, и
по условию, и 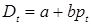 , можно подставить
, можно подставить 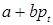 и
и 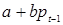 соответственно вместо
соответственно вместо 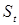 и
и 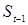 в (1.13) получим
в (1.13) получим
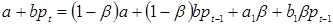 ,
,
откуда
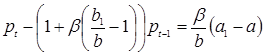 . (1.14)
. (1.14)
Частное решение (1.14) - 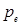 - цена равновесия. Общее решение соответствующего однородного уравнения:
- цена равновесия. Общее решение соответствующего однородного уравнения:
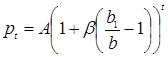 ,
,
и, таким образом, общее решение:
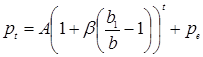 , (1.15)
, (1.15)
где 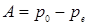 – начальное отклонение. Условие стабильности:
– начальное отклонение. Условие стабильности:
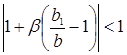 , (1.16)
, (1.16)
то есть
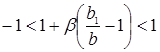
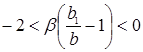 .
.
Разделив обе части на 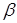 и прибавим
и прибавим 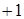 , получим:
, получим:
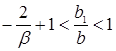 . (1.17)
. (1.17)
Если учесть первоначальное условие условие стабильности Теоремы о рыночном равновесии 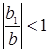 , то
, то
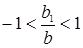 . (1.18)
. (1.18)
Поскольку 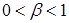 , получим 2 > 2.
, получим 2 > 2.
Таким образом
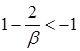 . (1.19)
. (1.19)
Следовательно неравенство (1.17) менее строгое, чем неравенство (1.18). Таким образом, использование адаптивных ожиданий делает модель более стабильной. Применение адаптивных ожиданий является одним из классических приемов стабилизации траектории динамической системы. Однако следует отметить тот факт, что не все динамические системы одинаково реагируют на введение этой стратегии управления. Известны случаи, когда адаптивные ожидания оказывались недостаточно рациональными для совершенствования механизмов управления, и приводили к обратному результату – снижению стабильности за счет сужения ее интервалов.





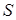 реагирует на изменение цены
реагирует на изменение цены 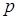 с лагом в один период, в то время как спрос
с лагом в один период, в то время как спрос 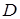 определяется ценой, и обе эти зависимости линейны:
определяется ценой, и обе эти зависимости линейны: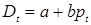 ,
,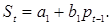
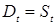 ,
,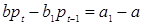 . (1.1)
. (1.1)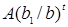 , а частное решение (1.1):
, а частное решение (1.1):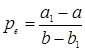 .
.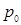 известно,
известно, 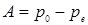 .
.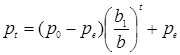 . (1.2)
. (1.2)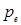 установлено, то
установлено, то 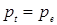 , то есть цена фиксируется на уровне
, то есть цена фиксируется на уровне 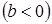 , а предложение - положительный
, а предложение - положительный 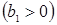 . Таким образом,
. Таким образом, 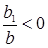 , и цена будет производить колебательные движения вокруг своего равновесного значения. Эти периодические колебания могут осуществляться с увеличивающимся, постоянным или уменьшающимся периодом (рис. 1.3.), в зависимости от соотношения
, и цена будет производить колебательные движения вокруг своего равновесного значения. Эти периодические колебания могут осуществляться с увеличивающимся, постоянным или уменьшающимся периодом (рис. 1.3.), в зависимости от соотношения 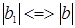 | (символ
| (символ 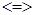 означает «меньше, равно или больше»), то есть в зависимости от того, превосходит ли угол наклона кривой спроса, угол наклона кривой предложения.
означает «меньше, равно или больше»), то есть в зависимости от того, превосходит ли угол наклона кривой спроса, угол наклона кривой предложения.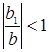 , то есть
, то есть 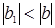 .
.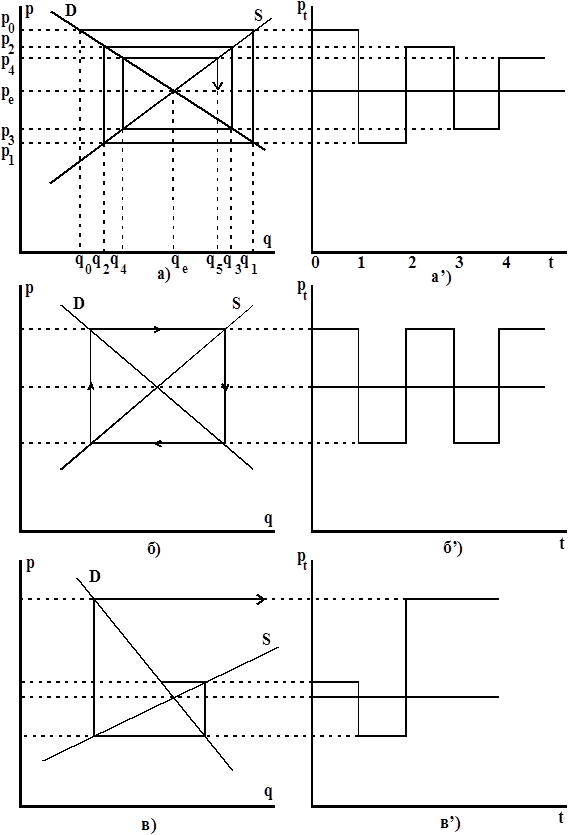
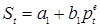 , (1.3)
, (1.3)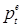 - цена, ожидаемая производителями, то есть цена, которая установится, по их мнению, на момент реализации продукции. Теорема о рыночном равновесии предполагает в качестве основного допущения, что
- цена, ожидаемая производителями, то есть цена, которая установится, по их мнению, на момент реализации продукции. Теорема о рыночном равновесии предполагает в качестве основного допущения, что 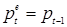 .
.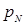 понимается цена, которая, по мнению производителя, рано или поздно установится на рынке. Поэтому, если текущая цена отличается от нормальной, они считают, что смогут изменить ее в дальнейшем. Другими словами
понимается цена, которая, по мнению производителя, рано или поздно установится на рынке. Поэтому, если текущая цена отличается от нормальной, они считают, что смогут изменить ее в дальнейшем. Другими словами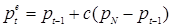 ,
, 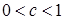 . (1.4)
. (1.4)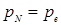 , и
, и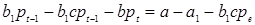 , (1.5)
, (1.5)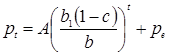 . (1.6)
. (1.6)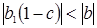 . (1.7)
. (1.7)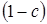 в 1.7 положительно и меньше единицы, так как
в 1.7 положительно и меньше единицы, так как 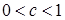 . Значит абсолютное значение
. Значит абсолютное значение 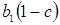 меньше, чем абсолютное значение
меньше, чем абсолютное значение 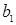 . Сравнив с первоначальной теоремой о рыночном равновесии, получим следующие результаты:
. Сравнив с первоначальной теоремой о рыночном равновесии, получим следующие результаты: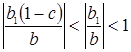 ,
,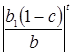 стремится к нулю быстрее, чем модуль
стремится к нулю быстрее, чем модуль 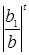 .
.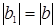 , то
, то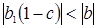 .
.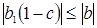 , даже при
, даже при 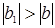 .
.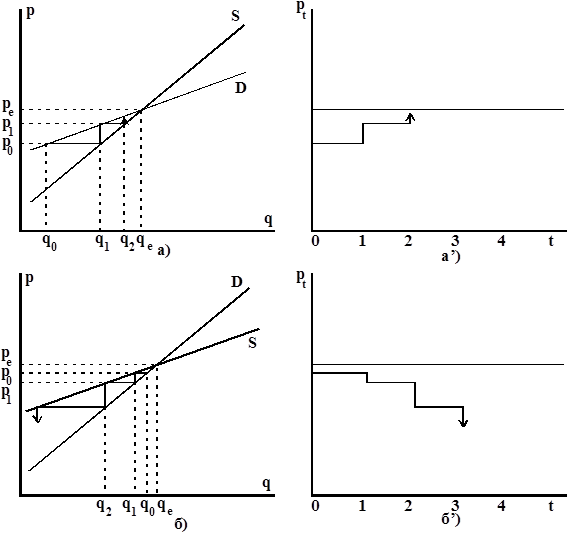
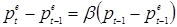 , (1.8)
, (1.8)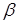 - положительный коэффициент меньше единицы.
- положительный коэффициент меньше единицы.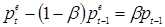 (1.9)
(1.9)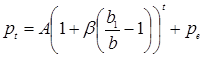 . (1.10)
. (1.10)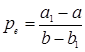 . (1.11)
. (1.11)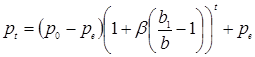 . (1.12)
. (1.12)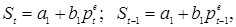
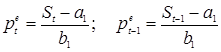 .
.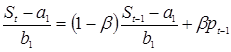 ,
,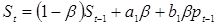 . (1.13)
. (1.13)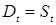 для всех
для всех  по условию, и
по условию, и 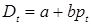 , можно подставить
, можно подставить 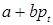 и
и 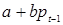 соответственно вместо
соответственно вместо 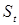 и
и 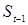 в (1.13) получим
в (1.13) получим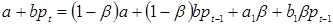 ,
,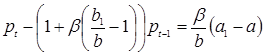 . (1.14)
. (1.14)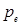 - цена равновесия. Общее решение соответствующего однородного уравнения:
- цена равновесия. Общее решение соответствующего однородного уравнения: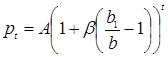 ,
,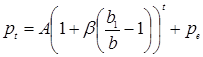 , (1.15)
, (1.15)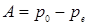 – начальное отклонение. Условие стабильности:
– начальное отклонение. Условие стабильности: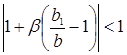 , (1.16)
, (1.16)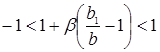
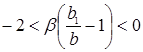 .
.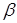 и прибавим
и прибавим 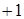 , получим:
, получим: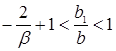 . (1.17)
. (1.17)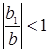 , то
, то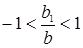 . (1.18)
. (1.18)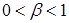 , получим 2 > 2.
, получим 2 > 2.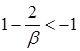 . (1.19)
. (1.19)

