Простейшая динамическая модель с мультипликатором
Как известно из Кейнсианской макроэкономики в замкнутой модели увеличение  автономных инвестиций (или в более общем случае автономных расходов) приводит к увеличению национального дохода в соответствии с уравнением мультипликатора
автономных инвестиций (или в более общем случае автономных расходов) приводит к увеличению национального дохода в соответствии с уравнением мультипликатора
 ,
,
где  - маргинальная (предельная) склонность к потреблению. В этом случае, если первоначальное значение величины равновесного дохода было
- маргинальная (предельная) склонность к потреблению. В этом случае, если первоначальное значение величины равновесного дохода было  , новое значение точки равновесия составит
, новое значение точки равновесия составит

Этот результат, однако, не говорит ничего относительно движения от старой точки равновесия к новой – мы не знаем, будет ли доход двигаться по направлению к равновесию или нет. Только динамическая модель может разъяснить этот вопрос. Обычным предположением является то, что потребление зависит от дохода с лагом в один период, то есть
 . (2.1)
. (2.1)
В предположении, что инвестиции полностью автономны и в начальный момент времени изменяются с  до
до  (и сохраняют этот уровень во всех последующих периодах):
(и сохраняют этот уровень во всех последующих периодах):
 . (2.2)
. (2.2)
Уравнение
 (2.3)
(2.3)
замыкает модель.
Подставляя (2.1) и (2.2) в (2.3) получим следующее уравнение:
 , (2.4)
, (2.4)
решением которого является
 (2.5)
(2.5)
Новое равновесное значение дохода  и начальное
и начальное  различаются на величину
различаются на величину  . Поскольку
. Поскольку
 ,
,
выражение 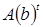 стремится к нулю, а доход движется (монотонно) по направлению к новому состоянию равновесия. На рис. 2.1 представлено графическое отображение данного подхода. Начальный уровень инвестирования
стремится к нулю, а доход движется (монотонно) по направлению к новому состоянию равновесия. На рис. 2.1 представлено графическое отображение данного подхода. Начальный уровень инвестирования  (предполагаем, что
(предполагаем, что  ) и
) и  – его новый уровень (сдвиг был преувеличен для графической наглядности). Соответствующие уровни равновесия
– его новый уровень (сдвиг был преувеличен для графической наглядности). Соответствующие уровни равновесия  и
и  соответственно. Рассмотрим динамику процесса. В периоде
соответственно. Рассмотрим динамику процесса. В периоде  потребление, зависящее от дохода в периоде
потребление, зависящее от дохода в периоде 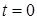 , составляет
, составляет 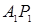 . Добавляя его к новому уровню инвестирования
. Добавляя его к новому уровню инвестирования  получаем доход в периоде
получаем доход в периоде  ,
,  . При помощи «линии 45°» мы переносим этот сегмент на ось и получаем точку
. При помощи «линии 45°» мы переносим этот сегмент на ось и получаем точку  . В периоде
. В периоде  потребление
потребление  и доход
и доход  ; при помощи «линии 45°» получаем точку
; при помощи «линии 45°» получаем точку  и т.д. Как видно из рис. 2.1. траектория системы монотонно сходится к точке
и т.д. Как видно из рис. 2.1. траектория системы монотонно сходится к точке  .
.
Рассмотренный случай предполагал, что инвестирование было полностью автономным. Рассмотрим инвестирование, которое является частично автономным, и частично зависящим от дохода (с лагом в один период) в соответствии с предельной склонностью к инвестированию  ,
,  .
.
Формула (2.2) преобразовывается к виду:
 ,
,
а уравнение (2.4) преобразовывается к виду:
 ,
,
решением которого является:
 .
.
Поскольку и  , и
, и  положительны, траектория монотонна. Стабильность требует
положительны, траектория монотонна. Стабильность требует  , то есть
, то есть
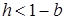 . (2.6.)
. (2.6.)

Рисунок 2.1. Простой динамический мультипликатор.
Поскольку  – предельная склонность к накоплению, условие (2.6) говорит о том, что предельная склонность к инвестированию должна быть меньше для того, чтобы равновесие было стабильным. Отметим, что из этого следует
– предельная склонность к накоплению, условие (2.6) говорит о том, что предельная склонность к инвестированию должна быть меньше для того, чтобы равновесие было стабильным. Отметим, что из этого следует 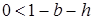 , что определяет положительность акселератора
, что определяет положительность акселератора  .
.
Модель внешней торговли
Как пример дальнейшего совершенствования мультипликаторной модели рассмотрим мультипликатор внешней торговли. Импорт является функцией дохода, а экспорт предполагается полностью экзогенным (позднее будет рассмотрена модель мультипликатора с внешнеторговой отдачей, снимающая это ограничение). В открытой экономике, совокупное предложение определяется как сумма национального продукта  и импорта
и импорта  ; совокупный спрос определяется как национальное потребление
; совокупный спрос определяется как национальное потребление  плюс национальное инвестирование
плюс национальное инвестирование 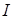 плюс экспорт
плюс экспорт  . Балансовым соотношением является уже не выражение
. Балансовым соотношением является уже не выражение  , а выражение
, а выражение  или
или  . В этом случае формальная модель выглядит следующим образом:
. В этом случае формальная модель выглядит следующим образом:
 ,
,
 ,
,
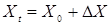 ,
,
 ,
,
 .
.
Подставляя первые четыре выражения в балансовое соотношение, получим
 , (2.7)
, (2.7)
решение которого имеет вид:
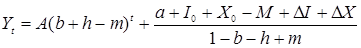 . (2.8)
. (2.8)
Отметим, что мультипликатором является  . «Потери» от импорта представлены величиной
. «Потери» от импорта представлены величиной  – предельной склонностью к импорту.
– предельной склонностью к импорту.
Сумма  очевидно превосходит
очевидно превосходит  . Условие стабильности имеет вид
. Условие стабильности имеет вид  или
или  , что гарантирует положительность мультипликатора
, что гарантирует положительность мультипликатора  . Условие стабильности также может быть преобразовано к виду
. Условие стабильности также может быть преобразовано к виду
 , (2.9)
, (2.9)
то есть предельная склонность к инвестированию должна быть меньше суммы предельной склонности к накоплению и предельной склонности к импорту.
Интересное следствие возникает при рассмотрении вопроса о полной сбалансированности торговли. Предположим, что первоначально торговля сбалансирована (то есть  ) и экспорт автономно увеличивается. Доход увеличивается в соответствии с мультипликатором внешней торговли и также увеличивается импорт, поскольку он – возрастающая функция дохода. Будет ли (вынужденное) увеличение в импорте полностью компенсировать (эндогенное) увеличение экспорта?
) и экспорт автономно увеличивается. Доход увеличивается в соответствии с мультипликатором внешней торговли и также увеличивается импорт, поскольку он – возрастающая функция дохода. Будет ли (вынужденное) увеличение в импорте полностью компенсировать (эндогенное) увеличение экспорта?
Формально имеем:

и
 .
.
Откуда следует, что  в том и только в том случае, когда
в том и только в том случае, когда  , то есть
, то есть  .
.
Налогообложение
Рассмотрим последнее совершенствование модели мультипликатора – модель с налогообложением. Для упрощения задачи предположим, что для закрытой экономики налогообложение является простой линейной функцией дохода,
 .
.
Потребление в этом случае – это функция чистого дохода  , который в нашей упрощенной модели может быть вычислен как
, который в нашей упрощенной модели может быть вычислен как  , где
, где  – уровень обесценения,
– уровень обесценения,  – трансфертные платежи, оба предполагаются эндогенными. Отсюда имеем
– трансфертные платежи, оба предполагаются эндогенными. Отсюда имеем
 ,
,
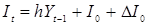 ,
,
 , (2.10)
, (2.10)
 ,
,
 ,
,
где  – правительственные расходы. Простой подстановкой с последующим приведением подобных получаем
– правительственные расходы. Простой подстановкой с последующим приведением подобных получаем
 ,
,
решение которого имеет вид:
 .
.
Поскольку и  , и
, и  – положительны, траектория будет монотонной. Мультипликатор с налогообложением
– положительны, траектория будет монотонной. Мультипликатор с налогообложением  меньше мультипликатора без учета налогообложения
меньше мультипликатора без учета налогообложения 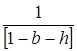 . Условие стабильности
. Условие стабильности
 (2.11)
(2.11)
является менее строгим, чем выражение (2.9), поэтому введение в модель налогообложения делает ее более стабильной.





 автономных инвестиций (или в более общем случае автономных расходов) приводит к увеличению национального дохода в соответствии с уравнением мультипликатора
автономных инвестиций (или в более общем случае автономных расходов) приводит к увеличению национального дохода в соответствии с уравнением мультипликатора ,
, - маргинальная (предельная) склонность к потреблению. В этом случае, если первоначальное значение величины равновесного дохода было
- маргинальная (предельная) склонность к потреблению. В этом случае, если первоначальное значение величины равновесного дохода было  , новое значение точки равновесия составит
, новое значение точки равновесия составит
 . (2.1)
. (2.1) до
до  (и сохраняют этот уровень во всех последующих периодах):
(и сохраняют этот уровень во всех последующих периодах): . (2.2)
. (2.2) (2.3)
(2.3) , (2.4)
, (2.4) (2.5)
(2.5) и начальное
и начальное  различаются на величину
различаются на величину  . Поскольку
. Поскольку ,
,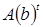 стремится к нулю, а доход движется (монотонно) по направлению к новому состоянию равновесия. На рис. 2.1 представлено графическое отображение данного подхода. Начальный уровень инвестирования
стремится к нулю, а доход движется (монотонно) по направлению к новому состоянию равновесия. На рис. 2.1 представлено графическое отображение данного подхода. Начальный уровень инвестирования  (предполагаем, что
(предполагаем, что  ) и
) и  – его новый уровень (сдвиг был преувеличен для графической наглядности). Соответствующие уровни равновесия
– его новый уровень (сдвиг был преувеличен для графической наглядности). Соответствующие уровни равновесия  и
и  соответственно. Рассмотрим динамику процесса. В периоде
соответственно. Рассмотрим динамику процесса. В периоде  потребление, зависящее от дохода в периоде
потребление, зависящее от дохода в периоде 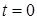 , составляет
, составляет 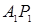 . Добавляя его к новому уровню инвестирования
. Добавляя его к новому уровню инвестирования  получаем доход в периоде
получаем доход в периоде  . При помощи «линии 45°» мы переносим этот сегмент на ось и получаем точку
. При помощи «линии 45°» мы переносим этот сегмент на ось и получаем точку  . В периоде
. В периоде  потребление
потребление  и доход
и доход  ; при помощи «линии 45°» получаем точку
; при помощи «линии 45°» получаем точку  и т.д. Как видно из рис. 2.1. траектория системы монотонно сходится к точке
и т.д. Как видно из рис. 2.1. траектория системы монотонно сходится к точке  ,
,  .
. ,
, ,
, .
. , и
, и  , то есть
, то есть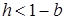 . (2.6.)
. (2.6.)
 – предельная склонность к накоплению, условие (2.6) говорит о том, что предельная склонность к инвестированию должна быть меньше для того, чтобы равновесие было стабильным. Отметим, что из этого следует
– предельная склонность к накоплению, условие (2.6) говорит о том, что предельная склонность к инвестированию должна быть меньше для того, чтобы равновесие было стабильным. Отметим, что из этого следует 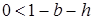 , что определяет положительность акселератора
, что определяет положительность акселератора  .
. и импорта
и импорта  ; совокупный спрос определяется как национальное потребление
; совокупный спрос определяется как национальное потребление  плюс национальное инвестирование
плюс национальное инвестирование 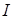 плюс экспорт
плюс экспорт  . Балансовым соотношением является уже не выражение
. Балансовым соотношением является уже не выражение  , а выражение
, а выражение  или
или  . В этом случае формальная модель выглядит следующим образом:
. В этом случае формальная модель выглядит следующим образом: ,
, ,
,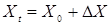 ,
, ,
, .
. , (2.7)
, (2.7)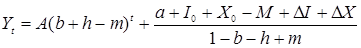 . (2.8)
. (2.8) . «Потери» от импорта представлены величиной
. «Потери» от импорта представлены величиной  – предельной склонностью к импорту.
– предельной склонностью к импорту. очевидно превосходит
очевидно превосходит  или
или  , что гарантирует положительность мультипликатора
, что гарантирует положительность мультипликатора  . Условие стабильности также может быть преобразовано к виду
. Условие стабильности также может быть преобразовано к виду , (2.9)
, (2.9) ) и экспорт автономно увеличивается. Доход увеличивается в соответствии с мультипликатором внешней торговли и также увеличивается импорт, поскольку он – возрастающая функция дохода. Будет ли (вынужденное) увеличение в импорте полностью компенсировать (эндогенное) увеличение экспорта?
) и экспорт автономно увеличивается. Доход увеличивается в соответствии с мультипликатором внешней торговли и также увеличивается импорт, поскольку он – возрастающая функция дохода. Будет ли (вынужденное) увеличение в импорте полностью компенсировать (эндогенное) увеличение экспорта?
 .
. в том и только в том случае, когда
в том и только в том случае, когда  , то есть
, то есть  .
. .
. , который в нашей упрощенной модели может быть вычислен как
, который в нашей упрощенной модели может быть вычислен как  , где
, где  – уровень обесценения,
– уровень обесценения,  – трансфертные платежи, оба предполагаются эндогенными. Отсюда имеем
– трансфертные платежи, оба предполагаются эндогенными. Отсюда имеем ,
,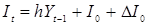 ,
, , (2.10)
, (2.10) ,
, ,
, – правительственные расходы. Простой подстановкой с последующим приведением подобных получаем
– правительственные расходы. Простой подстановкой с последующим приведением подобных получаем ,
, .
. , и
, и  меньше мультипликатора без учета налогообложения
меньше мультипликатора без учета налогообложения 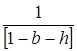 . Условие стабильности
. Условие стабильности (2.11)
(2.11)


