Объединяя (3.10) и (3.12) получаем все возможные случаи, которые могут быть условно отображены на графике (рис. 3.1), согласно Самуэльсону.
На диаграмме изображены функция 
 (кривая
(кривая  ) и функция
) и функция 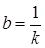 (кривая
(кривая  ). Поскольку
). Поскольку  , нас интересует только та часть положительного квадранта, которая находится под пунктирной линией (именно поэтому и не отображена верхняя часть гиперболы
, нас интересует только та часть положительного квадранта, которая находится под пунктирной линией (именно поэтому и не отображена верхняя часть гиперболы  ). Можно выделить четыре области (помним, что действительные корни положительны).
). Можно выделить четыре области (помним, что действительные корни положительны).
Область A. Любая точка в этой области лежит под функцией 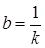 и над функцией
и над функцией 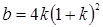 . Это графическое представление неравенств
. Это графическое представление неравенств  . Следовательно, согласно (3.10) и (3.12) условие стабильности выполняется, и корни действительные. Система будет проявлять монотонную сходимость к равновесному значению
. Следовательно, согласно (3.10) и (3.12) условие стабильности выполняется, и корни действительные. Система будет проявлять монотонную сходимость к равновесному значению 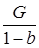 .
.
Область B. Любая точка этой области удовлетворяет неравенствам  . Условие стабильности выполняется и корни комплексные. Результатом являются затухающие колебания вокруг точки равновесия.
. Условие стабильности выполняется и корни комплексные. Результатом являются затухающие колебания вокруг точки равновесия.

Рисунок 3.1. Диаграмма мультипликатора-акселератора Самуэльсона.
Область C. Имеем  . Условие стабильности не выполняется и корни комплексные. Результат – взрывные колебания относительно равновесного значения.
. Условие стабильности не выполняется и корни комплексные. Результат – взрывные колебания относительно равновесного значения.
Область D. В этой области  . Условие стабильности не выполняется и корни действительные. Результатом является монотонная расходимость от точки равновесия.
. Условие стабильности не выполняется и корни действительные. Результатом является монотонная расходимость от точки равновесия.
Для того чтобы полностью завершить исследование необходимо рассмотреть точки, которые лежат на линиях, разграничивающих выделенные области. Поскольку  и
и 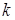 являются положительные константы в данной модели, и
являются положительные константы в данной модели, и  , необходимо исключить из рассмотрения точки на оси
, необходимо исключить из рассмотрения точки на оси 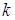 , на оси
, на оси  , начало координат, и точку
, начало координат, и точку  .
.
1. Точки на границе между  и
и 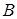 . Здесь выполняется
. Здесь выполняется  , то есть действительный корень кратности два
, то есть действительный корень кратности два  . Поскольку условие стабильности
. Поскольку условие стабильности  выполняется, этот корень меньше единицы. Поэтому функция
выполняется, этот корень меньше единицы. Поэтому функция  будет доминирующей при
будет доминирующей при  , и траектория, в конечном счете, монотонно будет сходиться к равновесию.
, и траектория, в конечном счете, монотонно будет сходиться к равновесию.
2. Точки, попавшие на границу между 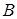 и
и  . Здесь имеем
. Здесь имеем  и
и  , то есть комплексные корни с единичным модулем, которые вызывают колебания с фиксированной амплитудой. Это, так сказать, траектория, разделяющая стабильность и нестабильность.
, то есть комплексные корни с единичным модулем, которые вызывают колебания с фиксированной амплитудой. Это, так сказать, траектория, разделяющая стабильность и нестабильность.
3. Точки, лежащие на границе областей 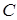 и
и  . Здесь мы имеем
. Здесь мы имеем 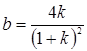 ,
,  , то есть корень кратности два, больший единицы. В результате - траектория, которая, в конечном счете, сведется к монотонной расходимости доминирующей компонентой
, то есть корень кратности два, больший единицы. В результате - траектория, которая, в конечном счете, сведется к монотонной расходимости доминирующей компонентой  .
.
Глава 5. Динамика поведения открытой экономики
Олигополия Курно
Вообще говоря, все экономические системы, даже наиболее простые из них, должны описываться системами уравнений. Тот факт, что многие из них исследуются в виде единственного уравнения, объясняется тем, что сведение системы уравнений к единственному уравнению напрашивается целиком естественно (то есть требуются только прямые подстановки без предшествующих преобразований), и этот метод гораздо проще, чем методы анализа систем уравнений. К примеру, однородная часть модели мультипликатора:
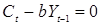 ,
,
 ,
,
 ,
,
имеет характеристическое уравнение

где  , и так далее. Однако прямая подстановка первых двух уравнений в третье является более очевидной и более простой альтернативой. С другой стороны, существуют экономические системы, у которых после такого приведения остается пара-тройка уравнений, для которых с успехом могут применяться методы анализа систем уравнений.
, и так далее. Однако прямая подстановка первых двух уравнений в третье является более очевидной и более простой альтернативой. С другой стороны, существуют экономические системы, у которых после такого приведения остается пара-тройка уравнений, для которых с успехом могут применяться методы анализа систем уравнений.
Общие положения, позволяющие описать поведение фирмы в статичных условиях, выводятся, прежде всего, благодаря допущению о том, что цена одного из продуктов несколько увеличивается, а также результатам анализа влияния этого роста на общую политику фирмы. Подобные положения следовало непосредственно выразить с помощью понятий динамики, если бы можно было предположить, например, что ожидаемая цена некоторого определенного продукта несколько повысится в некотором определенном периоде в будущем, скажем, речь шла бы о цене товара  которая, согласно ожиданиям, была установлена в периоде, наступающем через
которая, согласно ожиданиям, была установлена в периоде, наступающем через  периодов. Можно было бы рассматривать это как рост цены продукта
периодов. Можно было бы рассматривать это как рост цены продукта  . Применяя правила, пригодные для условий статики, прежде всего, следует уяснить, что неизбежно увеличение планируемого выпуска продукта
. Применяя правила, пригодные для условий статики, прежде всего, следует уяснить, что неизбежно увеличение планируемого выпуска продукта  . Это может служить результатом или увеличения количества применяемых ресурсов, или уменьшения выпуска других продуктов, или того и другого вместе. Увеличение количества применяемых ресурсов может наблюдаться в текущий момент или планироваться. Выпускаемые продукты, количество которых уменьшается, могут быть как одинаковыми, но изготавливаться в различных периодах (
. Это может служить результатом или увеличения количества применяемых ресурсов, или уменьшения выпуска других продуктов, или того и другого вместе. Увеличение количества применяемых ресурсов может наблюдаться в текущий момент или планироваться. Выпускаемые продукты, количество которых уменьшается, могут быть как одинаковыми, но изготавливаться в различных периодах ( ), так и разными (
), так и разными ( или
или  ). Далее всегда есть вероятность того, что некоторые из выпускаемых продуктов окажутся дополняющими по отношению к
). Далее всегда есть вероятность того, что некоторые из выпускаемых продуктов окажутся дополняющими по отношению к  , так что их производство будет соответственно расширено; вероятно также (хотя эта вероятность и меньше), что некоторые из применяемых ресурсов окажутся регрессивными по отношению к продукту
, так что их производство будет соответственно расширено; вероятно также (хотя эта вероятность и меньше), что некоторые из применяемых ресурсов окажутся регрессивными по отношению к продукту  , поэтому их будет использоваться меньше.
, поэтому их будет использоваться меньше.
Все это очень хорошо, но тем не менее вопрос о том, что происходит, когда ожидаемая цена определенного товара для определенного периода в будущем изменяется, это не тот вопрос, который должен нас сильно занимать. Наблюдаются случаи, довольно успешно объясняемые с помощью проведенного выше анализа; можно, например, усмотреть широкую применимость этого анализа в отношении такого, скажем, события, как объявление референдума, но это не типичный случай. Анализ экономической динамики предпочтительнее использовать в иных целях.
Изменения цен, последствия которых мы изучали при разработке статической теории, были изменениями реальных цен. И здесь нам также следовало бы иметь возможность изучить последствия изменения реальных цен, а не просто заниматься результатами изменений в ожиданиях. Теперь перед нами такого рода изменение рыночных цен, которое можно изучать путем непосредственного использования обычных положений: текущий выпуск продукции рассматривается как выпуск определенной продукции в определенном периоде, так что последствия изменения цен на такую продукцию можно выявить, применяя прежние правила. С точки зрения настоящего исследования это значит, что речь идет об изменении цен при данных ценовых ожиданиях. Нельзя допускать, что изменение в уровне текущих цен обусловливает иные ценовые ожидания, даже если это ожидания точно такой же цены. Иначе говоря, изменение цены должно рассматриваться как чисто временное изменение.
Итак, если есть необходимость непосредственно применять в анализе основные правила статики, то необходимо удержаться от рассмотрения всякого рода изменений в уровне рыночных цен, кроме тех изменений, которые, как предполагается, носят временный характер. Нельзя учесть, как данные условия сказываются на ожиданиях. И все-таки, если мы хотим, чтобы настоящая теория привела к полезным выводам, необходимо рассмотреть это влияние.
Как представляется, можно выделить три вида воздействий, которым могут быть подвержены ценовые ожидания. Воздействия первого вида отличаются совершенно неэкономическим характером: это погодные условия, политические события, состояние здоровья людей, их «психология». Второго вида воздействия носят экономический характер, однако, они все-таки еще не связаны тесно с действительным движением цен. Это обычные рыночные «суеверия», с одной стороны, а также сообщения, связанные с будущим движением спроса и предложения (например, сводки об урожае), с другой.
Воздействия третьего вида выражаются в действительном движении цен, прошлом и настоящем, и как раз о последнем можно сказать больше всего.
В соответствии с целью нашего исследования, необходимо считать, что изменения ценовых ожиданий, связанные с воздействиями первого и второго видов, являются автономными. На текущем состоянии экономики эти воздействия могут, видимо, сказаться каким-либо таинственным косвенным образом, но нам нечего и думать как-то учесть это. Не следует забывать, что ценовые ожидания подвержены влиянию независимых факторов, в противном случае не стоило бы об этом и говорить.
Влияние действительных цен на ценовые ожидания, то есть рациональные, обоснованные предположения о ценах, которые установятся в ближайшем будущем, заслуживает дальнейшего анализа, но в этом случае нельзя указать простых приемов исследования. Даже если исключить из рассмотрения независимые факторы, придется обсудить два вопроса: влияние на ценовые ожидания нынешних цен и влияние прошлых цен. Это влияние весьма различно, и очень важно, какими ценами ожидания определяются сильнее.
Прошлые цены — это прошлые цены, поэтому они, с точки зрения нынешнего положения дел, являются просто данными; если их влияние на ценовые ожидания преобладает, то и эти ожидания можно рассматривать как данные. С такого случая мы начали: изменение текущих цен не служит причиной перемен в ценовых ожиданиях; оно считается временным. Но как только прошлые цены перестают играть определяющую роль, мы должны допустить, что текущие цены так или иначе сказываются на ожиданиях. При этом подобное влияние текущих цен может отличаться различной интенсивностью и сказываться во многих различных направлениях.
Введем в анализ характеристику меры воздействия, которое мы изучаем. Если исключить возможность того, что изменение текущей цены продукта может так или иначе сказаться на ценах товара  , которые, как ожидается, установятся в различных периодах в будущем, и если также исключить возможность воздействия данного изменения текущей цены на ожидаемые в будущем цены прочих товаров или факторов производства (оба эти допущения очень серьезны), тогда мы сможем классифицировать данные случаи в соответствии с эластичностью ожиданий. Мы определяем эластичность ожиданий некоторого лица, связанных с ценой товара
, которые, как ожидается, установятся в различных периодах в будущем, и если также исключить возможность воздействия данного изменения текущей цены на ожидаемые в будущем цены прочих товаров или факторов производства (оба эти допущения очень серьезны), тогда мы сможем классифицировать данные случаи в соответствии с эластичностью ожиданий. Мы определяем эластичность ожиданий некоторого лица, связанных с ценой товара  , как отношение пропорционального увеличения ожидаемых в будущем цен товара
, как отношение пропорционального увеличения ожидаемых в будущем цен товара  , к пропорциональному увеличению текущей цены. Таким образом, если ожидания жестко неэластичны (эластичность ожиданий равна нулю), то перед нами случай, когда ожидания заданы. Если эластичность ожиданий равна единице, то изменение уровня текущих цен вызовет изменение (в том же направлении и в той же пропорции) ожидаемых цен. Если раньше предполагалось, что цены останутся без изменений, то теперь предполагается, что они сохраняются без изменений на новом уровне.
, к пропорциональному увеличению текущей цены. Таким образом, если ожидания жестко неэластичны (эластичность ожиданий равна нулю), то перед нами случай, когда ожидания заданы. Если эластичность ожиданий равна единице, то изменение уровня текущих цен вызовет изменение (в том же направлении и в той же пропорции) ожидаемых цен. Если раньше предполагалось, что цены останутся без изменений, то теперь предполагается, что они сохраняются без изменений на новом уровне.
Считается, что цены изменяются непрерывно. Как очевидно, речь здесь идет о двух основных случаях. Однако полезно провести также различие между «промежуточным» случаем, когда эластичность ожиданий меньше единицы и больше нуля, и двумя «крайними» случаями, когда эластичность ожиданий больше единицы и когда эластичность ожиданий отрицательна. Эластичность ожиданий будет больше единицы, если изменения текущих цен носят такой характер, что люди считают себя способными распознать направление этих изменений и стремятся экстраполировать события; эластичность ожиданий будет отрицательной, если они строят противоположные догадки, полагая, будто данные изменения служат кульминацией в развитии событий.
Если, с точки зрения предпринимателя, эластичность ценовых ожиданий в отношении товара  равна единице (считается, что цена этого товара изменяется непрерывно), то повышение текущей цены товара
равна единице (считается, что цена этого товара изменяется непрерывно), то повышение текущей цены товара 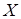 вызовет одинаковое повышение всех его ожидаемых цен. Как мы обнаружили, изучая условия статики, изменение цен товаров, образующих некий товарный набор, позволяет считать этот набор единичным товаром, соответственно, все закономерности экономического поведения остаются в отношении данного набора товаров справедливыми, как если бы это был единичный товар. Если эластичность ожиданий равна единице, то повышение текущей цены товара
вызовет одинаковое повышение всех его ожидаемых цен. Как мы обнаружили, изучая условия статики, изменение цен товаров, образующих некий товарный набор, позволяет считать этот набор единичным товаром, соответственно, все закономерности экономического поведения остаются в отношении данного набора товаров справедливыми, как если бы это был единичный товар. Если эластичность ожиданий равна единице, то повышение текущей цены товара 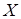 , установившейся на рынке, должно в целом вызвать увеличение планируемого выпуска товара
, установившейся на рынке, должно в целом вызвать увеличение планируемого выпуска товара  . Здесь не остается возможностей для замещения во времени, так что с данной точки зрения фактор времени можно не учитывать. Закономерности составления производственного плана в точности совпадают с закономерностями, управляющими поведением фирмы в статичных условиях — будет обязательно наблюдаться расширение выпуска товара
. Здесь не остается возможностей для замещения во времени, так что с данной точки зрения фактор времени можно не учитывать. Закономерности составления производственного плана в точности совпадают с закономерностями, управляющими поведением фирмы в статичных условиях — будет обязательно наблюдаться расширение выпуска товара  , когда либо растет объем применяемых ресурсов того или иного вида в том или ином периоде, либо происходит замещение товаром
, когда либо растет объем применяемых ресурсов того или иного вида в том или ином периоде, либо происходит замещение товаром 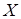 других товаров (других в физическом смысле, а не в смысле выпуска одного и того же товара в разных периодах).
других товаров (других в физическом смысле, а не в смысле выпуска одного и того же товара в разных периодах).
Если рассматривать планируемый выпуск товара 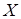 в целом, то он должен возрасти, однако нет, разумеется, причины, по которой это возрастание будет распределяться одинаково по всем периодам. Есть особые основания, чтобы предположить обратное. Дополнительный выпуск, который можно обеспечить за текущий период, а также выпуск, планируемый на ближайшие периоды, обычно оказываются незначительными. То первоначальное оснащение предприятия, которым располагает предприниматель в период составления плана, обыкновенно охватывает почти законченные изделия, намеченные к выпуску в ближайшем и чуть более отдаленном будущем. Так как подобные почти законченные изделия могут храниться на предприятии лишь в ограниченном количестве, «подвижность» подобного рода выпуска по отношению к изменениям цены будет обязательно небольшой. Однако расширение выпуска, относящееся к отдаленному будущему, не наталкивается на подобное ограничение, точнее, это ограничение становится все менее заметным, по мере того как процесс производства «отодвигается» в будущее.
в целом, то он должен возрасти, однако нет, разумеется, причины, по которой это возрастание будет распределяться одинаково по всем периодам. Есть особые основания, чтобы предположить обратное. Дополнительный выпуск, который можно обеспечить за текущий период, а также выпуск, планируемый на ближайшие периоды, обычно оказываются незначительными. То первоначальное оснащение предприятия, которым располагает предприниматель в период составления плана, обыкновенно охватывает почти законченные изделия, намеченные к выпуску в ближайшем и чуть более отдаленном будущем. Так как подобные почти законченные изделия могут храниться на предприятии лишь в ограниченном количестве, «подвижность» подобного рода выпуска по отношению к изменениям цены будет обязательно небольшой. Однако расширение выпуска, относящееся к отдаленному будущему, не наталкивается на подобное ограничение, точнее, это ограничение становится все менее заметным, по мере того как процесс производства «отодвигается» в будущее.
Классическая модель олигополии Курно (Cournot) сформулированная им в 1939 до сих пор рассматривается во многих учебниках по микроэкономике, где говорится о том, что она может быть интерпретирована в терминах современной теории игр. Также становится возможным дать динамическую интерпретацию этой модели, учитывая то, что вложил в нее Курно, когда писал о ее стабильности. Стабильность модели заключается в использовании процесса обучения, во время которого каждая фирма наблюдает за уровнем производства другой фирмы, и, таким образом, совершенствует свое собственное представление о поведении системы в целом. Точнее, в любом периоде  каждая фирма
каждая фирма  наблюдает за уровнем производства остальных фирм и предполагает, что эти величины останутся неизменными в периоде
наблюдает за уровнем производства остальных фирм и предполагает, что эти величины останутся неизменными в периоде 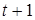 . Таким образом, фирма
. Таким образом, фирма  будет выбирать свой уровень производства исходя из своего мнения и данной рынком кривой спроса.
будет выбирать свой уровень производства исходя из своего мнения и данной рынком кривой спроса.
Интересным фактом, впервые обнаруженным Теохарисом в 1960 году, является то, что при формализации динамического поведения траектория дохода больше не остается стабильной, когда фирм больше, чем две.
Рассмотрим рынок с 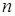 олигополистическими фирмами, производящими однородную продукцию, и линейной кривой спроса
олигополистическими фирмами, производящими однородную продукцию, и линейной кривой спроса
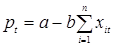 , (5.1)
, (5.1)
где  ,
, 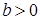 и
и  – реальный уровень производства фирмы i в период времени
– реальный уровень производства фирмы i в период времени  . Также сделаем предположение, что предельные себестоимости
. Также сделаем предположение, что предельные себестоимости  постоянны для линейных кривых затрат
постоянны для линейных кривых затрат 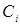 каждой фирмы.
каждой фирмы.
Таким образом, фирма устанавливает рыночную цену, основанную на своих представлениях о том, что уровни производства других фирм останутся неизменными, то есть
 , (5.2)
, (5.2)
на основании того, что каждая фирма  определяет
определяет  так, чтобы максимизировать свою прибыль
так, чтобы максимизировать свою прибыль  .
.
Условия первого порядка для локального максимума  , то есть
, то есть
 ,
,
или
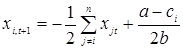 . (5.3)
. (5.3)
Условия второго порядка  несомненно выполняются, поскольку в предположении, что
несомненно выполняются, поскольку в предположении, что  . Следовательно, уравнение (5.3) дает требуемое решение. Рассмотрим дуополию, в которой условия первого рода образуют систему неоднородных разностных уравнений
. Следовательно, уравнение (5.3) дает требуемое решение. Рассмотрим дуополию, в которой условия первого рода образуют систему неоднородных разностных уравнений
 , (5.4)
, (5.4)
 .
.
Характеристическое уравнение однородной части системы (5.4):
 .
.
Откуда 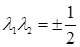 . Поэтому траектория будет сходиться по направлению к точке равновесия, которая получается подстановкой
. Поэтому траектория будет сходиться по направлению к точке равновесия, которая получается подстановкой  в систему (5.3). Простые вычисления дают
в систему (5.3). Простые вычисления дают  .
.
Это подтверждает утверждение Курно о том, что равновесие стабильно, то есть «если один из производителей собьется с пути, ведущего к его истинной заинтересованности, он снова будет на него повернут последовательностью реакций, постоянно уменьшающими амплитуду» [1]. Но это также содержит опасность того, что то, что выполняется для двумерных систем, не выполняется для n-мерных. Рассмотрим матрицу системы (5.3)
 (5.5)
(5.5)
и характеристическое уравнение
 . (5.6)
. (5.6)
Легко проверить, что  – корень характеристического уравнения. Действительно. Представьте себе характеристический детерминант, и добавьте, к примеру, его первые
– корень характеристического уравнения. Действительно. Представьте себе характеристический детерминант, и добавьте, к примеру, его первые  столбцов к последнему (известно, что это не изменит детерминанта). Все элементы последнего столбца будут
столбцов к последнему (известно, что это не изменит детерминанта). Все элементы последнего столбца будут  . Теперь, если мы положим
. Теперь, если мы положим  , то получим детерминант со столбцом из нулей, что, собственно, и означает, что детерминант равен нулю. Отсюда следует, что
, то получим детерминант со столбцом из нулей, что, собственно, и означает, что детерминант равен нулю. Отсюда следует, что 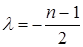 – корень характеристического уравнения.
– корень характеристического уравнения.
Из этого следует, что для  система имеет корень равный –1 (неправильные колебания с постоянной амплитудой), для
система имеет корень равный –1 (неправильные колебания с постоянной амплитудой), для  эти колебания будут взрывными. Таким образом, система стабильна только при
эти колебания будут взрывными. Таким образом, система стабильна только при  .
.
Эти результаты, однако, должны быть переосмыслены с учетом использования регулирующих лагов, различных предположений о формировании ожиданий, и т.п.






 (кривая
(кривая  ) и функция
) и функция 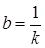 (кривая
(кривая  ). Поскольку
). Поскольку  , нас интересует только та часть положительного квадранта, которая находится под пунктирной линией (именно поэтому и не отображена верхняя часть гиперболы
, нас интересует только та часть положительного квадранта, которая находится под пунктирной линией (именно поэтому и не отображена верхняя часть гиперболы  ). Можно выделить четыре области (помним, что действительные корни положительны).
). Можно выделить четыре области (помним, что действительные корни положительны).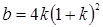 . Это графическое представление неравенств
. Это графическое представление неравенств  . Следовательно, согласно (3.10) и (3.12) условие стабильности выполняется, и корни действительные. Система будет проявлять монотонную сходимость к равновесному значению
. Следовательно, согласно (3.10) и (3.12) условие стабильности выполняется, и корни действительные. Система будет проявлять монотонную сходимость к равновесному значению 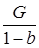 .
. . Условие стабильности выполняется и корни комплексные. Результатом являются затухающие колебания вокруг точки равновесия.
. Условие стабильности выполняется и корни комплексные. Результатом являются затухающие колебания вокруг точки равновесия.
 . Условие стабильности не выполняется и корни комплексные. Результат – взрывные колебания относительно равновесного значения.
. Условие стабильности не выполняется и корни комплексные. Результат – взрывные колебания относительно равновесного значения. . Условие стабильности не выполняется и корни действительные. Результатом является монотонная расходимость от точки равновесия.
. Условие стабильности не выполняется и корни действительные. Результатом является монотонная расходимость от точки равновесия. и
и 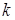 являются положительные константы в данной модели, и
являются положительные константы в данной модели, и  , необходимо исключить из рассмотрения точки на оси
, необходимо исключить из рассмотрения точки на оси 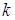 , на оси
, на оси  , начало координат, и точку
, начало координат, и точку  .
. и
и 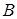 . Здесь выполняется
. Здесь выполняется  , то есть действительный корень кратности два
, то есть действительный корень кратности два  . Поскольку условие стабильности
. Поскольку условие стабильности  выполняется, этот корень меньше единицы. Поэтому функция
выполняется, этот корень меньше единицы. Поэтому функция  будет доминирующей при
будет доминирующей при  , и траектория, в конечном счете, монотонно будет сходиться к равновесию.
, и траектория, в конечном счете, монотонно будет сходиться к равновесию. . Здесь имеем
. Здесь имеем  и
и  , то есть комплексные корни с единичным модулем, которые вызывают колебания с фиксированной амплитудой. Это, так сказать, траектория, разделяющая стабильность и нестабильность.
, то есть комплексные корни с единичным модулем, которые вызывают колебания с фиксированной амплитудой. Это, так сказать, траектория, разделяющая стабильность и нестабильность.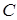 и
и  . Здесь мы имеем
. Здесь мы имеем 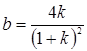 ,
,  , то есть корень кратности два, больший единицы. В результате - траектория, которая, в конечном счете, сведется к монотонной расходимости доминирующей компонентой
, то есть корень кратности два, больший единицы. В результате - траектория, которая, в конечном счете, сведется к монотонной расходимости доминирующей компонентой  .
.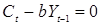 ,
, ,
, ,
,
 , и так далее. Однако прямая подстановка первых двух уравнений в третье является более очевидной и более простой альтернативой. С другой стороны, существуют экономические системы, у которых после такого приведения остается пара-тройка уравнений, для которых с успехом могут применяться методы анализа систем уравнений.
, и так далее. Однако прямая подстановка первых двух уравнений в третье является более очевидной и более простой альтернативой. С другой стороны, существуют экономические системы, у которых после такого приведения остается пара-тройка уравнений, для которых с успехом могут применяться методы анализа систем уравнений. которая, согласно ожиданиям, была установлена в периоде, наступающем через
которая, согласно ожиданиям, была установлена в периоде, наступающем через  периодов. Можно было бы рассматривать это как рост цены продукта
периодов. Можно было бы рассматривать это как рост цены продукта  ), так и разными (
), так и разными ( или
или  ). Далее всегда есть вероятность того, что некоторые из выпускаемых продуктов окажутся дополняющими по отношению к
). Далее всегда есть вероятность того, что некоторые из выпускаемых продуктов окажутся дополняющими по отношению к  , так что их производство будет соответственно расширено; вероятно также (хотя эта вероятность и меньше), что некоторые из применяемых ресурсов окажутся регрессивными по отношению к продукту
, так что их производство будет соответственно расширено; вероятно также (хотя эта вероятность и меньше), что некоторые из применяемых ресурсов окажутся регрессивными по отношению к продукту  , поэтому их будет использоваться меньше.
, поэтому их будет использоваться меньше. , которые, как ожидается, установятся в различных периодах в будущем, и если также исключить возможность воздействия данного изменения текущей цены на ожидаемые в будущем цены прочих товаров или факторов производства (оба эти допущения очень серьезны), тогда мы сможем классифицировать данные случаи в соответствии с эластичностью ожиданий. Мы определяем эластичность ожиданий некоторого лица, связанных с ценой товара
, которые, как ожидается, установятся в различных периодах в будущем, и если также исключить возможность воздействия данного изменения текущей цены на ожидаемые в будущем цены прочих товаров или факторов производства (оба эти допущения очень серьезны), тогда мы сможем классифицировать данные случаи в соответствии с эластичностью ожиданий. Мы определяем эластичность ожиданий некоторого лица, связанных с ценой товара  , к пропорциональному увеличению текущей цены. Таким образом, если ожидания жестко неэластичны (эластичность ожиданий равна нулю), то перед нами случай, когда ожидания заданы. Если эластичность ожиданий равна единице, то изменение уровня текущих цен вызовет изменение (в том же направлении и в той же пропорции) ожидаемых цен. Если раньше предполагалось, что цены останутся без изменений, то теперь предполагается, что они сохраняются без изменений на новом уровне.
, к пропорциональному увеличению текущей цены. Таким образом, если ожидания жестко неэластичны (эластичность ожиданий равна нулю), то перед нами случай, когда ожидания заданы. Если эластичность ожиданий равна единице, то изменение уровня текущих цен вызовет изменение (в том же направлении и в той же пропорции) ожидаемых цен. Если раньше предполагалось, что цены останутся без изменений, то теперь предполагается, что они сохраняются без изменений на новом уровне. равна единице (считается, что цена этого товара изменяется непрерывно), то повышение текущей цены товара
равна единице (считается, что цена этого товара изменяется непрерывно), то повышение текущей цены товара 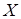 вызовет одинаковое повышение всех его ожидаемых цен. Как мы обнаружили, изучая условия статики, изменение цен товаров, образующих некий товарный набор, позволяет считать этот набор единичным товаром, соответственно, все закономерности экономического поведения остаются в отношении данного набора товаров справедливыми, как если бы это был единичный товар. Если эластичность ожиданий равна единице, то повышение текущей цены товара
вызовет одинаковое повышение всех его ожидаемых цен. Как мы обнаружили, изучая условия статики, изменение цен товаров, образующих некий товарный набор, позволяет считать этот набор единичным товаром, соответственно, все закономерности экономического поведения остаются в отношении данного набора товаров справедливыми, как если бы это был единичный товар. Если эластичность ожиданий равна единице, то повышение текущей цены товара  , когда либо растет объем применяемых ресурсов того или иного вида в том или ином периоде, либо происходит замещение товаром
, когда либо растет объем применяемых ресурсов того или иного вида в том или ином периоде, либо происходит замещение товаром  наблюдает за уровнем производства остальных фирм и предполагает, что эти величины останутся неизменными в периоде
наблюдает за уровнем производства остальных фирм и предполагает, что эти величины останутся неизменными в периоде 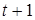 . Таким образом, фирма
. Таким образом, фирма 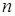 олигополистическими фирмами, производящими однородную продукцию, и линейной кривой спроса
олигополистическими фирмами, производящими однородную продукцию, и линейной кривой спроса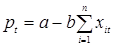 , (5.1)
, (5.1) ,
, 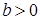 и
и  – реальный уровень производства фирмы i в период времени
– реальный уровень производства фирмы i в период времени  . Также сделаем предположение, что предельные себестоимости
. Также сделаем предположение, что предельные себестоимости  постоянны для линейных кривых затрат
постоянны для линейных кривых затрат 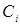 каждой фирмы.
каждой фирмы. , (5.2)
, (5.2) так, чтобы максимизировать свою прибыль
так, чтобы максимизировать свою прибыль  .
. , то есть
, то есть ,
,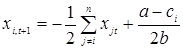 . (5.3)
. (5.3) несомненно выполняются, поскольку в предположении, что
несомненно выполняются, поскольку в предположении, что  . Следовательно, уравнение (5.3) дает требуемое решение. Рассмотрим дуополию, в которой условия первого рода образуют систему неоднородных разностных уравнений
. Следовательно, уравнение (5.3) дает требуемое решение. Рассмотрим дуополию, в которой условия первого рода образуют систему неоднородных разностных уравнений , (5.4)
, (5.4) .
. .
.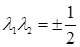 . Поэтому траектория будет сходиться по направлению к точке равновесия, которая получается подстановкой
. Поэтому траектория будет сходиться по направлению к точке равновесия, которая получается подстановкой  в систему (5.3). Простые вычисления дают
в систему (5.3). Простые вычисления дают  .
. (5.5)
(5.5) . (5.6)
. (5.6) – корень характеристического уравнения. Действительно. Представьте себе характеристический детерминант, и добавьте, к примеру, его первые
– корень характеристического уравнения. Действительно. Представьте себе характеристический детерминант, и добавьте, к примеру, его первые  столбцов к последнему (известно, что это не изменит детерминанта). Все элементы последнего столбца будут
столбцов к последнему (известно, что это не изменит детерминанта). Все элементы последнего столбца будут  . Теперь, если мы положим
. Теперь, если мы положим  , то получим детерминант со столбцом из нулей, что, собственно, и означает, что детерминант равен нулю. Отсюда следует, что
, то получим детерминант со столбцом из нулей, что, собственно, и означает, что детерминант равен нулю. Отсюда следует, что 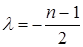 – корень характеристического уравнения.
– корень характеристического уравнения. система имеет корень равный –1 (неправильные колебания с постоянной амплитудой), для
система имеет корень равный –1 (неправильные колебания с постоянной амплитудой), для  эти колебания будут взрывными. Таким образом, система стабильна только при
эти колебания будут взрывными. Таким образом, система стабильна только при  .
.


