Эта модель, которая была построена Самуэльсоном (Samuelson) с учетом предположений Хансена (Hansen) в 1939 году, по сути, является простейшей мультипликаторно-акселераторной моделью определения динамики дохода в производственном цикле. В состав этой модели в качестве «ингредиентов» вошли функция потребления, функция инвестирования (в которой присутствует как автономное, так и вынужденное инвестирование) и их соотношение, которое определяет состояние равновесия – равновесный доход. Функция потребления имеет вид
 , (3.1)
, (3.1)
где потребление зависит от национального дохода с лагом в один период. Константа  – это предельная склонность к потреблению. Поскольку в модель включено инвестирование, мы выделяем вынужденное инвестирование
– это предельная склонность к потреблению. Поскольку в модель включено инвестирование, мы выделяем вынужденное инвестирование  и автономное инвестирование
и автономное инвестирование 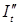 .
.
Тогда
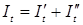 . (3.2)
. (3.2)
Автономное инвестирование (а фактически – общественные расходы) предполагаем постоянными:
 , (3.3)
, (3.3)
где 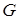 – положительная константа.
– положительная константа.
Вынужденное инвестирование зависит от изменений спроса на товары потребления в соответствии с принципом акселерации:
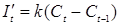 , (3.4)
, (3.4)
где  – коэффициент акселерации (в соответствии с терминологией Хансена).
– коэффициент акселерации (в соответствии с терминологией Хансена).
Состояние равновесия
 (3.5)
(3.5)
замыкает модель.
Простая подстановка дает следующее разностное уравнение второго порядка:
 . (3.6)
. (3.6)
Решение этого функционального уравнения дает поведение во времени национального дохода. Подставив его в уравнения (3.1) и (3.4) получим траектории потребления и инвестирования.
Частное решение уравнения (3.6) может быть легко найдено через  , откуда
, откуда
 . (3.7)
. (3.7)
Эту величину мы получаем применяя мультипликатор  к автономным расходам
к автономным расходам 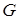 . Это частное решение определяет (стационарное) состояние равновесия национального дохода.
. Это частное решение определяет (стационарное) состояние равновесия национального дохода.
Отклонение от этого равновесного значения будет задаваться общим решением однородного уравнения, соответствующего уравнению (6.6), то есть
 .
.
Характеристическое уравнение:
 . (3.8)
. (3.8)
Проведем качественный анализ уравнения (3.8). Для начала применим условия стабильности. Анализ показывает, что модель, заданная разностным уравнением второго порядка, проявляет стабильное поведение при выполнении следующих условий:
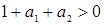 ,
,
 ,
,
 .
.
Для рассматриваемого случая условия стабильности:
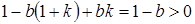 ,
,
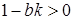 , (3.9)
, (3.9)
 .
.
Первое неравенство выполняется, поскольку мы предположили, что предельная склонность к потреблению меньше единицы (и это эмпирически правдоподобное утверждение); третье неравенство также выполняется, так как левая часть – это сумма положительных величин. Таким образом, критическое неравенство – второе. Следовательно, можно сказать, что условие стабильности
 или
или 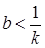 . (3.10)
. (3.10)
В случае если мы заинтересуемся установлением характера поведения (монотонное, колебательное, и т.д.), необходимо отметить, что последовательность знаков коэффициентов в (3.8) «+», «-», «+». Это означает, что не может возникнуть ни одного отрицательного корня. Таким образом, можно исключить из рассмотрения случай с возникновением «неправильных» колебаний. Следующий шаг – это вычислить дискриминант уравнения (3.8). Он равен
 , (3.11)
, (3.11)
и, таким образом,
 , если
, если  .
.
Откуда
 , когда
, когда  . (3.12)
. (3.12)





 , (3.1)
, (3.1) – это предельная склонность к потреблению. Поскольку в модель включено инвестирование, мы выделяем вынужденное инвестирование
– это предельная склонность к потреблению. Поскольку в модель включено инвестирование, мы выделяем вынужденное инвестирование  и автономное инвестирование
и автономное инвестирование 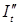 .
.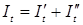 . (3.2)
. (3.2) , (3.3)
, (3.3)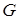 – положительная константа.
– положительная константа.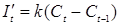 , (3.4)
, (3.4) – коэффициент акселерации (в соответствии с терминологией Хансена).
– коэффициент акселерации (в соответствии с терминологией Хансена). (3.5)
(3.5) . (3.6)
. (3.6) , откуда
, откуда . (3.7)
. (3.7) к автономным расходам
к автономным расходам  .
. . (3.8)
. (3.8)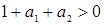 ,
, ,
, .
.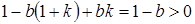 ,
,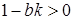 , (3.9)
, (3.9) .
. или
или 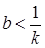 . (3.10)
. (3.10) , (3.11)
, (3.11) , если
, если  .
. . (3.12)
. (3.12)

