

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
¥
| k |
å
k =0
ckx = s (x),| x |< R. Положим
c 0= s (0).
x = 0,тогдаполучим:
¥
| k |
å
k =1
ckxk -1= s ¢(x),| x |< R,
| n |
x = 0.Тогда
c 1= s ¢(0).Продолжаяпроцессдифференцирования,
получим:
n! c = s (n)(0).
Тоесть,
cn =
s (n)(0)
n!
.Такимобразом,коэффициентыстепенногоряда
являются коэффициентами формулыТейлора длясуммыряда.
Поставимвопросы:еслидляпроизвольнойфункции
f (x),имеющей
бесконечноечислопроизводныхвточке
x = 0
построитьряд
¥ (k)
å f
(1) xk,
называемый рядомТейлора функции
1) гдеонбудетсходиться, и
f (x),то
k =0 k!
2) еслибудетсходиться,тобудетлисходитьсяксамойфункции f (x)?
| f |
1) ТаккакрядТейлора
¥ (k)
å
(0) xk –этостепеннойряд,тодлянего
k =0 k!
обычнымобразомможнонаходитьрадиусиинтервалсходимости.Тоесть,
R = lim| f (n)(0)|(n +1)
n ®¥
| f (n +1)(0)|.
2) ТаккакчастнаясуммарядаТейлора–этомногочленизформулы
Тейлора
n
å
k =0
f (k)(0) xk
k!
,торазностьмеждучастнойсуммойифункцией
f (x)
согласно формулеТейлораестьостаточныйчленформулыТейлора. Мы
егорассматриваливформеЛагранжа:
rn (x)=
f (n)(q x)
n!
xn,0< q < 1. Таким
образом,есливнутриинтерваласходимостиостаточный членформулы
Тейлорастремитсякнулюсростом n,тосуммаряда Тейлора совпадаетсисходнойфункцией,покоторойпостроенряд.И тогда говорят,что
функция
f (x)
представима в видерядаТейлора,тоесть
¥
f (x)= å
k =0
f (k)(0) xk.
k!
Примерыразложенияфункцийв рядыТейлора
Пример1. Рассмотримфункцию
|
|
ex. В соответствиис формулой
x x x 2 x 3 xn
Тейлора-Маклорена e
| rn (x)|£ e
=1+1!+ 2!+ 3!+×××+ n!+ rn (x),
× | x | n +1.
(n +1)!
где max{ x,0}
Сосчитаемрадиуссходимостистепенногоряда:
R = lim(n +1)!= lim(n +1)= ¥.
n ®¥ n!
n ®¥
Такимобразом, этотрядсходитсявовсехточкахвещественнойоси.Для
¥ xk
того,чтобывыяснить,будетлисходитьсяряд
å кфункции
| k! |
| | n +1
ex,заметим,
чтоприлюбомзначении
x ÎR
имеем | rn (x)|£ e | x |×
x ® 0 (n +1)!
при n ®¥.
| ¥ |
| å |
k
привсех
x ÎR.
k =0!
Пример 2. Рассмотрим функциюформулойТейлора-Маклорена
f (x) = sin x. В соответствии с
1 1 1
(-1) n +1
sin x = x -
x 3+
x 5+×××+
()
x 2 n -1+ r (x),
1! 3! 5! 2 n -1! n
где
| r (x)|£ | x |2 n +1.Тоесть,
R = lim
(2 n +1)! = ¥ и
rn (x)® 0
при n ®¥.
| n |
| ¥ |
n ®¥ (2 n -1)!
Следовательно,
sin x = å
| () |
x 2 n -1
привсех
x ÎR.
Пример 3. Рассмотрим функциюформулойТейлора-Маклорена
f (x) = cos x.
В соответствии с
111
(-1) n
cos x =1-
x 2+
x 4 -
x 6+×××+
()
x 2 n + r (x),
2! 4! 6! 2 n
| x |2(n +1)
! n
(2 n +2)!
где
| rn (x)|£ (2 n + 2)!. Тоесть,
¥ (
R = lim
n ®¥
-1) n
(2 n)!
= ¥ и
rn (x)® 0
при
n ®¥.Следовательно,
cos x = å
| () |
x 2 n
при всех
x ÎR.
Пример 4. Рассмотрим функцию
f (x) = (1+ x)a,
a ÏN. В
соответствиисформулойТейлора-Маклоренаприa ÏN
+ = +a
+ a a-
+ + a a- a- a- + +.
(1 x)a 1 x
(1) x 2
2!
...
(1)(2)...(
n!
n 1) xn
rn (x)
Найдемрадиуссходимостиэтогостепенногоряда:
R = lim
n +1
=1.
n ®¥ a - n
Дляоценкиостаточногочленапри n,большихилиравныхцелойчастиa,
формаЛагранжаостаточногочленагодитсятолькодля
x > 0.Вэтомслучае
имеем оценку:
| rn (x)|£ |a(a-1)(a- 2)...(a- n)| x |(n +1). Очевидно, что при
(n +1)!
0< x <1
имеем
rn (x)® 0
при n ®¥.Для отрицательныхзначений x
применяетсядругаяформа остаточногочлена. В результатедля | x |<1
справедливопредставление
|
|
(1+ x)a =1+
¥
å
n =1
a(a -1)(a - 2)...(a - n +1) xn.
n!
В случае,когда
a = m
– натуральноечисло,производныефункции
(1+ x) m
порядка выше, чем m, обращаются в 0. Следовательно,
коэффициентырядапристепеняхвыше m – нулевые, изначит,отряда
останетсятолькоконечнаясумма,содержащая
это имеетвид
m +1слагаемое.Разложение
(1 x) m 1
m m ( m -1)( m - 2)...( m - n +1) xn 1
m
Cnxn
+ = + å
n =1
= + å m,
n =1
| n! |
ПримерыприложенийрядовТейлора.
Представленныевпредыдущемпунктеканоническиеразложениямогут
служитьосновойдляполученияновыхразложений.Так,положив
a = -1в
последнем разложении, мы получим формулы суммы бесконечнойгеометрической прогрессии со знаменателем (- q):
1- q + q 2+...+ (- q) n +...=
1+ q
.Замениввэтойформуле q на(- q),получим:
1+ q + q 2+...+ qn +...=
1.
1- q
Заменим впоследней формуле q на
- t 2,мыполучимразложение
1+ t 2
¥
= å
n =0
(- t 2) n,
| t |<1. Последний ряд имеет радиус сходимости,
равный1.Вспомним,чтовнутриинтерваласходимостирядыможноинтегрироватьпочленноипроинтегрируемобечастипоследнегоравенствапо t от0до
| x |
| n =0 |
x, | x |<1,тогдаполучимразложение:
arctg x = å(-1) 2 n +1.
Еще легче получить разложение
ln(1+ x)= å (-1)
n +1 xn
,
если
| ¥ |
проинтегрировать почленно ряд
1- t + t 2+...+ (- t) n +...=
1+ t
внутри
интерваласходимости,тоесть при| t |<1.
Разложенияфункций
ex, sin x
и cos x врядыТейлора,справедливые
длявсехвещественных x,оказываютсятакимижеивслучае,когда x –
комплексноечисло.Пусть x = i × t,где i –мнимаяединица,тоесть,
i 2= -1,а
t – вещественноечисло.(Заметим,чтоТейлора:
i 3= - i,
i 4=1).Разложим
ei × t
вряд
2 3 4 5 6 7 2 4 6
ei × t = + i × t - t
- it + t
+ it - t
- it
+ = - t + t
– t + +
1
t 3 t 5
2! 3! 4! 5! 6! 7!
t 7
..... (1
2! 4! 6!
...)
+ i (t - 3!+ 5!- 7!+....)= cos t
+ i ×sin t.
Вотэтаформула,выражающаясвязьмежду
ex, sin x
иcos x вслучае
комплексныхпеременных, и называется формулой Эйлера.
РядыТейлораслужатдля приближения многихфункций.Деловтом,чтоарифметическиеоперации,которыепроводятсяточно–этооперацииумноженияначисло(аследовательно,ивозведениевцелуюположительнуюстепень)и сложение.Поэтомувычислениезначениймногих известных
|
|
функций,например,
ex,sin x,cos x,ln x, сводится к вычислениюзначений
близкихкэтимфункцияммногочленов–частныхсуммсоответствующихрядовТейлора.Этисуммызаложенывпрограммувычисленийнашихкалькуляторов.
ЧастныесуммырядаТейлора
n
å
k =0
f (k)(0) xk
k!
дляпроизвольнойфункции
f (x)можнополучатьс помощьюпрограммыMAXIMA.Длятого,чтобы
получить
n (k)
å f
(a)(x - a) k
дляконкретнойфункции
f (x),следуетнабрать
k =0 k!
taylor(f(x),x,a,n) и нажать Shift+Enter.
Пример. ДляполучениясуммыТейлора7-йстепенипостепеням(x -1)
для функции ln x
x
следует набрать taylor(log(x)/x,x,1,7). Мы получим
x -1-3(x -1)2/2+11(x -1)3/6-25(x -1)4/12+137(x -1)5/60-49(x -1)6/20+
+363(x -1)7/140+.
Сравнимполученныймногочлен(красныйграфик) сисходнойфункцией
ln x
x (синийграфик)на одномрисунке.Для этоговведем load(draw);
draw2d(color=blue, explicit(log(x)/x,x,0.2,2), color=red,
explicit (taylor(log(x)/x,x,1,7),x,0.2,2))
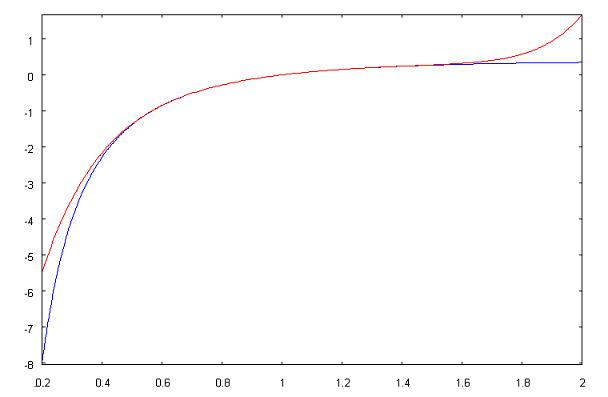
Мы видим,что красныйи синийграфикисливаютсяв окрестности
точки
x =1иудаляютсядруготдругаприудаленииаргументаотзначения1.
Этосвидетельствуетотом,чточастныесуммырядовТейлораприближают
функцию тольков окрестноститочки
x =1.
ТригонометрическиерядыФурье
Вразличныхотрасляхнауки,втомчисле,вфизикеприходитсяиметьдело с периодическимиявлениями.Простейшийпример– электрические
колебания. Периодической называется функция
f (x), для которой
существует такая величина,называемая периодом, что
f (x)=
f (x + T).
Простейшими T - периодическими функциями являются
тригонометрическиефункциивида
sin2p kx,cos2p kx,где k –целоечисло,
T T
называемые гармониками. Представлениепериодическойфункцииввиде
суммыгармоникназываетсягармоническиманализом.Вслучае,когдатакая
суммабесконечна,мыполучаемтригонометрическийряд, называемыйрядомФурье.
Итак, пусть непрерывная T - периодическая функция
f (x)
представлена в виде тригонометрического ряда:
| å |
cos2p kx + b
sin2p kx. Возникает вопрос: как найти
2 k =1 k
T k T
коэффициенты
a 0, ak, bk,
k Î N?
Воспользуемся тем,что гармоникиобладают следующимсвойством:
T /2
ò
- T /2
T /2
ò
- T /2
T /2
cos
sin
2p kx T
|
|
2p kx T
dx = 0,
dx = 0,
ò
- T /2
T /2
ò
- T /2
T /2
ò
- T /2
T /2
ò
cos2p lx sin2p mxdx = 0,
T T
cos2p lx cos2p mxdx = 0,
T T
sin2p lx sin2p mxdx = 0,
T T
cos22p lxdx = 2,
" l, m Î N,
" l, m ÎN, l ¹ m,
" l, m Î N, l ¹ m,
- T /2
T /2
ò
- T /2
T T
sin22p lxdx = 2.
T T
Теперьдлятого,чтобы,например,найтиравенства
am умножимобечасти
| å |
cos2p kx + b
sin2p kx
на cos2p mx
ипроинтегрируем
2 k =1 k
T k T T
наотрезке[- T /2, T /2].Сучетомсвойствгармониквправойчастиравенства
останется только слагаемое
a 2, а в левой части – выражение
| m |
T /2
ò
- T /2
f (x)cos
2p mx T
dx. Отсюдамыполучим
am.
Умножаянаsin2p mx
T
иинтегрируя,получим bm.
Адлятого,чтобыполучить
a 0,нужнопростопроинтегрироватьобе
части равенства
f (x)= a 0+ ¥ a
cos2p kx + b
sin2p kx
на отрезке
| å |
2 k =1 k
T k T
Таким образом, непрерывная периодическая функцияпредставима в видеследующеготригонометрическогорядаФурье:
f (x)
| å |
cos2p kx + b
sin2p kx, где
2 T /2
k =1
k T k T
2p kx
ak = T
ò
- T /2
f (x)cos T
dx,
k = 0,1,2,....,
b = 2
k T
T /2
ò
- T /2
f (x)sin
2p kx T
dx,
k =1,2,....
Вслучае,когдапериодическаяфункцияимеет точкиразрыва,еетакжеможнораскладыватьврядФурье,норавенствофункцииисуммырядабудеттольковточкахнепрерывностифункции.ВточкахразрыварядФурьебудетсходитьсякполусуммезначенийфункциислеваисправаотточкиразрыва:
¥
a 0+ å a
cos2p kx 0+ b
sin2p kx 0= 1(f (x
- 0)+ f (x
+ 0)).
2 k =1 k
T k T 2 0 0
ВозможноразложениефункцииврядФурьеспомощьюMAXIMы.Мы
получимвсе коэффициентырядаФурье дляфункции
f (x), заданнойна
отрезке[- T, T ]
и T -периодическипродолженнойнавсювещественнуюось,
если введем load(fourie); fourier (f(x),x,t) и нажмемShift+Enter.
Пример. Получим коэффициенты ряда Фурье для функции
f (x)= ex,-p £ x < p. Для этого введем load(fourie);fourier(%e^x,x,%pi),
нажмем Shift+Enterи получим
- e -p
)/p,
an = (n sinp n /(e p n 2+ e p)+ e p n sinp n /(n 2+1)-
-cosp n /(e p n 2+ e p)+ e p cosp n /(n 2+1))/p,
bn = (sinp n /(e p n 2+ e p)+ e p p sinp n /(n 2+1)-
- n cosp n /(e p n 2+ e p)+ e p n cosp n /(n 2+1))/p.
Мы видим,что коэффициентысодержатвыражения sinp n = 0и
cosp n = (-1) n. Поэтомупреобразуемкоэффициенты:
a 0=
e p - e -p,
p
| n |
e p),
| - |
| n |
e p).
| + |
Длятого,чтобынетольковычислитькоэффициентырядаФурье,нои
получитьразложениефункции
f (x), заданнойна отрезке[- T, T ]
и T -
периодическипродолженной на всювещественную ось врядФурье, следуетввести load(fourie);totalfourier(f(x),x,T) и нажать Shift+Enter.
Пример. ДляразложенияврядФурьефункцииизпредыдущегопримеравведем load(fourie);totalfourier(%e^x,x,%pi). Приэтомполучимразложение
¥
e -p (e p -1)(e p +1)å
– n =1
n (-1) n sin nx
|
|
n 2+1
¥
e -p (e p -1)(e p +1)å
+ n =1
(-1) n cos nx
n 2+1 +
p p
+ e -p (e p -1)(e p +1)
2p.
Следует отметить, что частные суммы ряда Фурье приближаютисходнуюфункциюне в конкретныхточках,а «всреднемпо отрезку».
Сравнимзаданнуюфункцию
y = ex,-p £ x £ p,и9-ючастнуюсуммуряда
Фурье на одном графике. Для этого сначала введем функцию
g (x),
совпадающуюс9-йчастнойсуммой,азатемнарисуемфункцию ex
(черным
цветом)ифункцию
[-p,p ]:
g (x)
(краснымцветом)наодномграфикенадотрезком
g(x):=-(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum((n*(-
1)^n*sin(n*x))/(n^2+1),n,1,9))/%pi+(%e^(-%pi)*(%e^%pi-
1)*(%e^%pi+1)*sum(((-1)^n*cos(n*x))/(n^2+1),n,1,9))/%pi+
(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1))/(2*%pi);
load(draw); draw2d(explicit(%e^x,x,-%pi,%pi), color=red,explicit(g(x),x,-%pi,%pi)).
В результате получимкартину
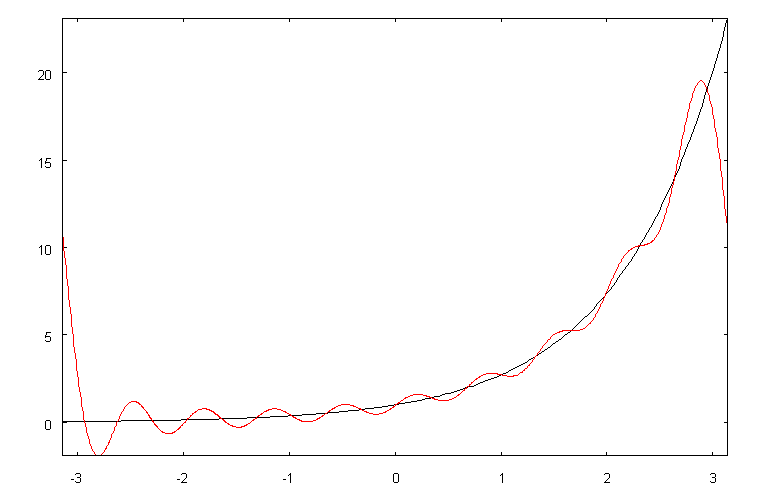
Здесь видно, что в конечных точках отрезка, где функция
y = ex,-p £ x £ p, припериодическомпродолжениис отрезка [-p,p ] в
другиеточкивещественнойоситерпитразрыв,графикчастнойсуммырядаФурье(краснаялиния)значительноотличаетсяотграфикаэкспоненциальнойфункции.Еслибратьчастнуюсуммусбольшимколичествомчленов,тографикчастнойсуммыбудеттеснееприближатьсякисходнойфункцииво
внутреннихточкахинтервала (-p,p),новблизиточек x = ±p
поведение
будет тем же из-за разрыва исходной функции при периодическомпродолжении.
ДИФФЕРЕНЦИАЛЬНЫЕУРАВНЕНИЯ
Дифференциальным уравнением называется соотношение вида
F (x, y (x), y ¢, y ¢,..., y (n))= 0. Решить дифференциальное уравнение – это
значит,определитьфункцию
y (x),удовлетворяющееэтомусоотношению,
возможно, в неявном или параметрическомвиде.
Простейшеедифференциальноеуравнениевида
y ¢(x)=
f (x)
мы уже
решали, так как находили
y (x)= ò f (x) dx. Мы знаем, что интеграл
определяетсясточностьюдопроизвольногопостоянногослагаемого.Тоесть
решение простейшего дифференциального уравнения содержит
произвольнуюпостоянную.Решенияболеесложныхдифференциальныхуравненийтакженаходятсясточностьюдопроизвольныхпостоянных.Любуюфункцию,удовлетворяющуюдифференциальномууравнению,мыбудемназывать частнымрешением этогоуравнения,совокупностьчастныхрешенийназовем общимрешением дифференциальногоуравнения.
Порядок дифференциального уравнения определяетсянаивысшимпорядком входящих в него производных. Поэтому дифференциальное
уравнениевида
F (x, y (x), y ¢, y ¢,..., y (n))= 0
считаетсядифференциальным
уравнением n -гопорядка.
Также,какнелюбаяфункцияможетбытьпроинтегрирована,ипредставленаввидеэлементарныхфункций,такинелюбоедифференциальноеуравнениеимеетрешение,выражающеесячерезэлементарныефункции.Классдифференциальныхуравнений,
интегрируемыхв квадратурах,узок.Мы изучимнесколькоклассов
дифференциальныхуравнений,интегрируемыхвквадратурах,атакжерассмотримнекоторыеприближенныеметодырешениядифференциальныхуравнений.Крометого,мырассмотримнекоторыезадачи,связанныесприменениемдифференциальныхуравнений.
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!