Семестр3элементытеориимножеств

СЕМЕСТР3ЭЛЕМЕНТЫТЕОРИИМНОЖЕСТВ

 

Понятие множества или совокупности принадлежиткчислупростейшихматематическихпонятий.Ононеимеетточногоопределения.Любоемножествозадаетсясвоимиэлементами.Примерамиявляютсямножествокнигвбиблиотекеилимножествостудентов,присутствующихназанятии.Обычномножествообозначаютзаглавнымилатинскимибуквами(A),аегоэлементыстрочнымилатинскимибуквами(a).То,чтоэлементпринадлежитмножеству,обозначаюттак:aÎA.ЕслиaнепринадлежитA,тоэтотфактобозначаюттак:aÏA.ЕсливсеэлементымножестваAпринадлежатмножествуB,тоA–подмножествомножестваB(AÌ B).

Чтобызадатьмножество,следуетилиперечислитьегоэлементы,или

указатьхарактеристическоесвойствоегоэлементов,тоестьтакоесвойство,которымобладаютвсеэлементымножестваитолькоони.Мыужезнакомысоследующимипримерамиподмножеств вещественныхчисел.

Примеры.

1. Множествонатуральныхчисел:N={1,2,3,…,n,n+1,…}.Иззаписи

следует,чтовсенатуральныечисла,начинаясдвойки,получаютсяприбавлениемединицы к предыдущемучислу.

2. Множествоцелыхчисел:Z={0, 1,–1, 2,–2,…,n, –n,…}.

3. Множество рациональных чисел: Q={ p | p ÎZ, q Î N}.

q

Вертикальнаячертаозначает,чтозанейуказываетсяхарактеристическоесвойствоэлементовмножества.

4. Рассмотрим множество C комплексных чисел:

C= { z = x + i y | x, y ÎR},гдеi– число,удовлетворяющеесвойству:

i2= -1.

Очевидно,чтотакогочисланесуществуетнадействительнойпрямой.Поэтомудляинтерпретациикомплексныхчиселиспользуютточкиплоскости,накоторойвведеныдвекоординатныеоси.Однасовпадаетсдействительнойпрямой,инанеепроецируютдействительнуючастькомплексногочисла(x). Другая–мнимаяось–перпендикулярнадействительнойоси,инанеепроецируюткоэффициентприi(мнимуючасть числа).

Множество действительных чисел R является подмножеством

множестваC(вслучае,когда

y = 0).Необходимостьвкомплексныхчислах

 

возникаетужетогда,когдамырешаемквадратноеуравнениеисталкиваемсясо случаемотрицательногодискриминанта.Например,решаяуравнение

t 2- 2 t + 5= 0

с отрицательным дискриминантом, мы получим корни

t 1,2=1± -4

или

t 1,2=1± 2i. В комплексной плоскостидва этих

комплексных числа выглядят так:

 

Очевидно,чтоNÌ ZÌ QÌ RÌ C.

 

 

Двамножестваравнытогда итолькотогда,когдасостоятиз однихитех

жеэлементов.Поэтому A = B

означает,что A Ì B иодновременно B Ì A.

 

Врамкахрассматриваемойматематическойтеориивводятдваисключительныхмножества:пустоемножество(Æ),несодержащееэлементов,иуниверсальноемножествоили«универсум»(U),содержащеевсе элементыданнойтеории.

 

Декартовопроизведениемножеств

A \ B = A Ç Bc.

 

Пусть A и B – подмножествамножестваRвещественныхчисел.

Декартовымпроизведениемэтихмножеств A ´ B

назовемтакоемножество

точекскоординатами(x,y)наплоскости

R2, что x Î A

иодновременно

y Î B. Например,если A представляетотрезок[0,2],а B –отрезок[-1,6],то

A ´ B

– этопрямоугольникс соответствующимисторонами.Аналогично

вводитсядекартовопроизведениетрехиболее множеств.

 

 

ЭЛЕМЕНТЫКОМБИНАТОРИКИ

 

 

РЯДЫ

Числовыеряды

 

 

Понятиепределапоследовательностидаетвозможностьввестипонятие

¥

числовогоряда–бесконечнойсуммывида

å ak,где

k =1

ak –общийчленряда.

Напервыйвзглядбесконечноесуммированиеневозможноужехотябывсилуконечностижизнилюбого,ктозанимаетсясуммированием.Выходизположенияследующий:бесконечнаясуммапонимаетсякак предел

n

последовательности

sn –конечных n - ных частныхсумм

 

¥

sn = å ak. Таким

k =1

образом,суммойряда

å ak будем называтьчисло

k =1

å k

n

s = lim a.

n ®¥ k =1

 

Рядназывается сходящимся,еслидлянегосуществуетконечнаясумма.Рядназывается расходящимся,еслисоответствующийпределчастныхсуммне существует или бесконечен.

 

Пример 1. Сосчитаем сумму ряда

¥

å qk, | q |<1. Имеем согласно

k =1

 

формулесуммыгеометрическойпрогрессии

 

sn =

n

å

k =1

qk = q × qn -1.Поскольку

q -1

 

qn ® 0

 

при n ®¥,получим

¥

å qk =

k =1

q.

1- q

Заметим, чтопри| q |³1соответствующийрядрасходится.

 

 

¥

Пример 2. Сосчитаемсуммуряда å 1

 

. Имеем

 

 

sn = 1 + 1

 

 

+...+ 1

k =1 k (k +1)

= 2-1+ 3- 2+...+ n +1- n =

1×2 2×3

n (n +1) 1×2 2×3

n (n +1)

=1- 1+ 1- 1+...+ 1- 1

=1- 1,

¥

2 2 3

n n +1

n +1

следовательно,å 1

 

=1.

k =1 k (k +1)

 

Необходимым признаком сходимости числового ряда является

¥

n

условие:lim a = 0.Доказываетсяэтолегко:пустьряд

n ®¥

å akk =1

сходится,тоесть

n

существует lim s = s. При n ®¥справедливо:

n ®¥

n -1® ¥. Следовательно,

n -1

lim s = s. Поскольку

n ®¥

sn - sn -1= an, то из1-гои 2-госвойствпределов

последовательностейимеем:

lim an = lim(sn - sn -1)= 0, что и требовалось

 

доказать.

n ®¥

n ®¥

 

å

Заметим,чтонеобходимоеусловиесходимостинеявляетсядостаточным.Тоесть,стремлениекнулюобщегочленаряданеобеспечиваетегосходимость.

 

Контрпример. Покажем,чторяд

¥ 1, называемыйгармоническим

k =1 k

рядом,расходится.Дляэтогорассмотримпоследовательностьчастныхсумм

s 2 n,то естьчастныесуммы

s 2, s 4, s 8,.....Присуммированиичленовконечной

суммы

 

s 2 n

сгруппируемрядомстоящиечленысуммы,начинаяот

до

2 l +1

2 l +1,привсех l =1,..., n -1:

 

sn =1+ 1+ (1+ 1)+ (1+...+ 1)+...+ (1

 

+...+

1)>

2 2 3 4 5 8

2 n -1+1 2 n

>1+ 1+ 2× 1+ 4× 1+...+ 2 n -1× 1

=1+ n × 1.

2 4 8 2 n 2

Таким образом,

lim s 2

=¥, и значит, предел последовательности

n ®¥ n

частныхсуммне можетбыть конечным.

 

 

Свойствачисловых рядов

 

 

Следующиесвойствасходящихсярядовочевиднымобразомследуютизсвойствпределовпоследовательностей.

¥ ¥ ¥ ¥

1. Пустьряды

 

¥

å ak и

k =1

å bkk =1

сходятся, причем

å ak = s,

k =1

å bk = s.

k =1

Тогдаряд

å(a × ak + b × bk)

k =1

также сходится, причем

 

¥

å(a × ak + b × bk)= a × s + b ×s.

k =1

 

 

2. Ряды

¥

å akk =1

¥

и å ak + Nk =1

 

сходятсяилирасходятсяодновременно,

 

причем

¥ ¥

å ak + N = å ak - sN.

k =1

k =1

 

Знакопеременные ряды

 

 

Длязнакопеременныхрядовприведенныепризнакисходимоститакжеможноприменять,нодляисследования абсолютнойсходимости. Делов

 

том,чтоеслиряд

 

¥

¥

å| ck |

k =1

 

сходится,тосходитсяиряд

¥

å ck,причемвэтом

k =1

случаеряд

å ck называетсяабсолютносходящимся.Такимобразом,если

k =1

 

имеетсязнакопеременныйряд

¥

å ck,имеетсмыслпроверитьвозможность

k =1

 

применениякакого-либопризнакасходимостикряду

 

¥

¥

å| ck |,иеслиусловия

k =1

сходимостивыполняются, исходныйряд

å ck сходитсяабсолютно.

k =1

 

 

Пример. Ряд

¥

å

k =1

(-1) k

k a

 

сходитсяабсолютноприa >1.

 

ПризнакЛейбницасходимостизнакочередующегосяряда. Пусть

членыположительнойпоследовательности

¥

ak,монотонноубывая,стремятся

k -1

кнулюпри k ®¥.Тогдаряд

å

k =1

(-1) ak

сходится.

Доказательство. Рассмотримпоследовательностьчетныхчастныхсумм

s 2 n = a 1- a 2+ a 3-......+ a 2 n -1- a 2 n = (a 1- a 2)+ (a 3- a 4)+...+ (a 2 n -1- a 2 n)> 0.

Очевидно,чтосростом n значения

s 2 n

возрастают.Теперьзапишемэтуже

частную сумму в ином виде:

s 2 n = a 1-(a 2- a 3)-......- (a 2 n -2- a 2 n -1)- a 2 n.

Очевидно,что

s 2 n < a 1.Такимобразом,мыимееммонотонновозрастающую

ограниченную сверху последовательность

s 2 n. По одному из свойств

последовательностей существует

lim s = s. Итак, последовательность

2 n

n ®¥

частныхсуммс четныминомерамиимеет предел.Чтоже с нечетнымичастнымисуммами?

 

Так как

s 2 n +1= s 2 n + a 2 n +1 и

lim a 2 n +1= 0, то существует

n ®¥

lim s 2 n +1= lim s 2 n + lim a 2 n +1= s. Следовательно,существуетlim sn = s.

n ®¥

n ®¥

n ®¥

n ®¥

 

 

Пример. Ряд

¥

å

k =1

(-1) k

k a

 

сходитсяпопризнакуЛейбницаприлюбом

 

a > 0.

В предыдущем примере, опираясь на интегральный признак, мы

показали,чтоэтотрядпри

a >1

сходитсяабсолютно.При 0<a £1

рядне

может абсолютносходиться.Ноон сходитсяпопризнакуЛейбница.

 

 

Ряд,сходящийся, нонесходящийсяабсолютно,называется условносходящимся.

 

Функциональныеряды

 

 

 

{ n }

Пусть f (x),

n ÎN

 

x Î M,

 

–последовательностьфункций,заданныхна

одномитомжемножестве,причемприкаждомзначении

¥

x 0Î M

числовой

ряд

 

¥

å fk (x 0)

k =1

сходится. Тогдамы можемрассматриватьфункциональныйряд

å fk (x)

k =1

намножестве M иисследоватьсвойствафункции

s (x)–суммы

ряда –на томже множестве M.

 

В связи с вопросамисходимостифункциональныхрядовотметимследующийиз теоремысравнения мажорантныйпризнак сходимости

функциональногоряда:если

$ an > 0такоечто

¥

" x Î M,

" n ÎN(| fn (x)|£ an)

ирядсположительнымичленами

 

¥

å akk =1

сходится,тофункциональныйряд

å fk (x)

k =1

абсолютносходится намножестве M.

 

Степенные ряды

Простейшимпримеромфункциональногорядаявляетсястепеннойряд–

¥

рядвида

å ck

k =0

(x - a) k. Числа

ck, k = 0,1,..., называются коэффициентами

степенногоряда.Посколькупростойзаменойпеременной x = x - a

¥

исходный

k

степеннойрядпревращаетсявряд

å

k =0

ckx,мыбудемрассматриватьтолько

 

 

степенныерядывида

¥

å

k =0

 

k

ckx. Очевидно,чтотакойрядобязательносходится

вточкедает

x = 0.Ответомнавопрособобластисходимостистепенногоряда

 

 

ТеоремаАбеля. Пустьряд

¥

å

k =0

 

k

ckx

 

сходитсявточке

 

x = x 1,тогдаон

сходится,причемабсолютно, при" x,| x |<| x 1|.

¥

k

Пустьряд

 

" x,| x |>| x 2|.

å

k =0

ckx

расходитсявточке

 

¥

x = x 2

,тогдаонрасходитсяпри

k

Доказательство.Так какряд

å ckx 1

сходится,тообщийчленэтогоряда

k =0

стремитсяк нулю, изначит,ограничен,то есть,

k

 

$ M > 0

 

k 1

тчо| cxk |£ M.

k

 

Пусть

| x |<| x 1|

 

тогда

| cxk |£ M x

k

x

 

.Таккакряд

¥ x

å

Mx

 

сходится,

 

то потеоремесравненияабсолютносходитсяряд

 

¥

k

å ckx 1

k =1 1

.

Таккак

 

¥

k

å ckx 2

k =0

 

 

расходится,то

 

¥

å

k =0

 

 

k

ckx

k =0

 

не может сходитьсянипри

какихзначениях

x, | x |>| x 2|,таккаквпротивномслучаеонбысходился,в

соответствии с доказаннойчастьютеоремы, ипри

x = x 2.

ИзтеоремыАбеляследует,в частности,чтообластьсходимости

¥

k

степенногоряда

å

k =0

ckx

представляетсобойнекоторыйинтервал(- R, R),а

областьрасходимости–внешностьэтогоинтервала.Чтокасаетсядвухточек x = ± R,являющихсяграницамиэтогоинтервала,тосходимостьилирасходимостьрядавэтихточкахследуетпроверятьдлякаждойфункциииндивидуально.

 

Число R называется радиусомсходимости степенногоряда.Интервал

(- R, R)

называется интерваломсходимости степенногоряда.

 

 

Способыопределениярадиуса сходимостистепенногоряда

 

1. В соответствии с признаком Даламбера если

| c xn +1| | c

|| x | ¥

| c || x |

lim

n +1

= lim

n +1

<1,то

å| cxk |

сходится,если

lim

n +1

>1,

n ®¥

| cnxn +1|

¥

å

n ®¥

 

 

k

| cn |

kk =0

n ®¥

| cn |

то ряд

k =0

| cxk |

расходится. Следовательно, при | x |= R

имеем:

lim| cn +1| R =1

 

или

 

R = lim

| cn |.

n ®¥

| cn |

n ®¥ | cn +1|

 

2. АналогичноиспользуяпризнакКоши, получим

R = 1.

n

lim n | c |

n ®¥

¥ xn

Пример 1.Найтиобластьсходимостистепенногоряда

å p. Найдем

n

n =1

 

радиуссходимости.Здесь

c = 1

 

. Следовательно,

R = lim(n +1) p

 

=1.

n np

 

Проверим сходимость в точке

n ®¥

 

x =1. Имеем ряд

np

¥

å p, который

 

 

сходится, если

 

 

p >1ирасходится,если

 

 

p £1.

n =1 n

 

Проверимсходимостьв точке

 

x = -1.Имеемряд

¥

å

n =1

(-1) n, который

np

сходится, если

p > 0

и расходится, если

p £ 0.

 

 

Замечание. Внутри интервала сходимости ряд можно почленноинтегрироватьидифференцироватьлюбоечислораз.Этозначит,чтоесли

¥ b ¥ b

k

k

å ckx = s (x),| x |< R,то1)

ò s (x) dx = å

ck ò xdx,| a |,| b |< R,

k =0

 

 

2)(s (x))(m)=

 

¥

å ck

k = m

a

 

(xk)(m),| x |< R.

k =0 a

 

Примерыразложенияфункцийв рядыТейлора

 

 

 

Пример1. Рассмотримфункцию

ex. В соответствиис формулой

x x x 2 x 3 xn

Тейлора-Маклорена e

 

 

| rn (x)|£ e

=1+1!+ 2!+ 3!+×××+ n!+ rn (x),

× | x | n +1.

(n +1)!

где max{ x,0}

 

Сосчитаемрадиуссходимостистепенногоряда:

R = lim(n +1)!= lim(n +1)= ¥.

n ®¥ n!

n ®¥

Такимобразом, этотрядсходитсявовсехточкахвещественнойоси.Для

¥ xk

того,чтобывыяснить,будетлисходитьсяряд

å кфункции

k!

k =0

| | n +1

ex,заметим,

 

чтоприлюбомзначении

x ÎR

имеем | rn (x)|£ e | x |×

 

x ® 0 (n +1)!

при n ®¥.

¥

å

Следовательно, ex = xk

k

 

 

привсех

 

x ÎR.

k =0!

 

 

 

Пример 2. Рассмотрим функциюформулойТейлора-Маклорена

f (x) = sin x. В соответствии с

 

1 1 1

(-1) n +1

sin x = x -

x 3+

x 5+×××+

()

x 2 n -1+ r (x),

1! 3! 5! 2 n -1! n

 

где

| r (x)|£ | x |2 n +1.Тоесть,

 

R = lim

(2 n +1)! = ¥ и

 

rn (x)® 0

 

при n ®¥.

n

(2 n +1)!

 

 

¥

(-1) n +1

n ®¥ (2 n -1)!

Следовательно,

sin x = å

()

n =12 n -1!

x 2 n -1

привсех

x ÎR.

 

 

 

Пример 3. Рассмотрим функциюформулойТейлора-Маклорена

f (x) = cos x.

 

В соответствии с

 

111

(-1) n

cos x =1-

x 2+

x 4 -

x 6+×××+

()

x 2 n + r (x),

2! 4! 6! 2 n

 

| x |2(n +1)

! n

 

(2 n +2)!

где

| rn (x)|£ (2 n + 2)!. Тоесть,

¥ (

R = lim

n ®¥

-1) n

 

(2 n)!

= ¥ и

rn (x)® 0

при

n ®¥.Следовательно,

cos x = å

()

n =02 n!

x 2 n

при всех

x ÎR.

 

 

Пример 4. Рассмотрим функцию

f (x) = (1+ x)a,

a ÏN. В

соответствиисформулойТейлора-Маклоренаприa ÏN

 

 

+ = +a

+ a a-

+ + a a- a- a- + +.

(1 x)a 1 x

(1) x 2

2!

...

(1)(2)...(

n!

n 1) xn

rn (x)

 

 

Найдемрадиуссходимостиэтогостепенногоряда:

 

R = lim

n +1

 

=1.

n ®¥ a - n

 

Дляоценкиостаточногочленапри n,большихилиравныхцелойчастиa,

формаЛагранжаостаточногочленагодитсятолькодля

x > 0.Вэтомслучае

 

имеем оценку:

| rn (x)|£ |a(a-1)(a- 2)...(a- n)| x |(n +1). Очевидно, что при

(n +1)!

0< x <1

имеем

rn (x)® 0

при n ®¥.Для отрицательныхзначений x

применяетсядругаяформа остаточногочлена. В результатедля | x |<1

 

справедливопредставление

 

(1+ x)a =1+

¥

å

n =1

a(a -1)(a - 2)...(a - n +1) xn.

n!

 

В случае,когда

a = m

– натуральноечисло,производныефункции

(1+ x) m

порядка выше, чем m, обращаются в 0. Следовательно,

коэффициентырядапристепеняхвыше m – нулевые, изначит,отряда

останетсятолькоконечнаясумма,содержащая

это имеетвид

m +1слагаемое.Разложение

 

 

(1 x) m 1

m m ( m -1)( m - 2)...( m - n +1) xn 1

m

Cnxn

+ = + å

n =1

= + å m,

n =1

 

n!

а полученнаяформуланосит название«биномНьютона».

 

 

ПримерыприложенийрядовТейлора.

Представленныевпредыдущемпунктеканоническиеразложениямогут

служитьосновойдляполученияновыхразложений.Так,положив

a = -1в

последнем разложении, мы получим формулы суммы бесконечнойгеометрической прогрессии со знаменателем (- q):

 

1- q + q 2+...+ (- q) n +...=

1+ q

 

.Замениввэтойформуле q на(- q),получим:

 

1+ q + q 2+...+ qn +...=

1.

1- q

 

Заменим впоследней формуле q на

- t 2,мыполучимразложение

 

 

1+ t 2

¥

= å

n =0

 

(- t 2) n,

 

| t |<1. Последний ряд имеет радиус сходимости,

равный1.Вспомним,чтовнутриинтерваласходимостирядыможноинтегрироватьпочленноипроинтегрируемобечастипоследнегоравенствапо t от0до

 

x

¥ 2 n +1

n =0

n

x, | x |<1,тогдаполучимразложение:

arctg x = å(-1) 2 n +1.

 

 

Еще легче получить разложение

ln(1+ x)= å (-1)

n +1 xn

,

 

если

¥

n =1 n

 

проинтегрировать почленно ряд

 

1- t + t 2+...+ (- t) n +...=

1+ t

 

внутри

интерваласходимости,тоесть при| t |<1.

 

 

 

Разложенияфункций

ex, sin x

и cos x врядыТейлора,справедливые

длявсехвещественных x,оказываютсятакимижеивслучае,когда x –

комплексноечисло.Пусть x = i × t,где i –мнимаяединица,тоесть,

i 2= -1,а

t – вещественноечисло.(Заметим,чтоТейлора:

i 3= - i,

i 4=1).Разложим

ei × t

вряд

2 3 4 5 6 7 2 4 6

ei × t = + i × t - t

- it + t

+ it - t

- it

+ = - t + t

– t + +

1

 

t 3 t 5

 

2! 3! 4! 5! 6! 7!

t 7

..... (1

 

2! 4! 6!

...)

+ i (t - 3!+ 5!- 7!+....)= cos t

+ i ×sin t.

 

 

Вотэтаформула,выражающаясвязьмежду

ex, sin x

иcos x вслучае

комплексныхпеременных, и называется формулой Эйлера.

 

 

РядыТейлораслужатдля приближения многихфункций.Деловтом,чтоарифметическиеоперации,которыепроводятсяточно–этооперацииумноженияначисло(аследовательно,ивозведениевцелуюположительнуюстепень)и сложение.Поэтомувычислениезначениймногих известных

функций,например,

ex,sin x,cos x,ln x, сводится к вычислениюзначений

близкихкэтимфункцияммногочленов–частныхсуммсоответствующихрядовТейлора.Этисуммызаложенывпрограммувычисленийнашихкалькуляторов.

 

ЧастныесуммырядаТейлора

n

å

k =0

f (k)(0) xk

k!

 

дляпроизвольнойфункции

f (x)можнополучатьс помощьюпрограммыMAXIMA.Длятого,чтобы

 

получить

n (k)

f

å

(a)(x - a) k

 

дляконкретнойфункции

 

f (x),следуетнабрать

k =0 k!

taylor(f(x),x,a,n) и нажать Shift+Enter.

 

Пример. ДляполучениясуммыТейлора7-йстепенипостепеням(x -1)

для функции ln x

x

 

следует набрать taylor(log(x)/x,x,1,7). Мы получим

x -1-3(x -1)2/2+11(x -1)3/6-25(x -1)4/12+137(x -1)5/60-49(x -1)6/20+

+363(x -1)7/140+.

Сравнимполученныймногочлен(красныйграфик) сисходнойфункцией

ln x

x (синийграфик)на одномрисунке.Для этоговведем load(draw);

draw2d(color=blue, explicit(log(x)/x,x,0.2,2), color=red,

explicit (taylor(log(x)/x,x,1,7),x,0.2,2))

 

 

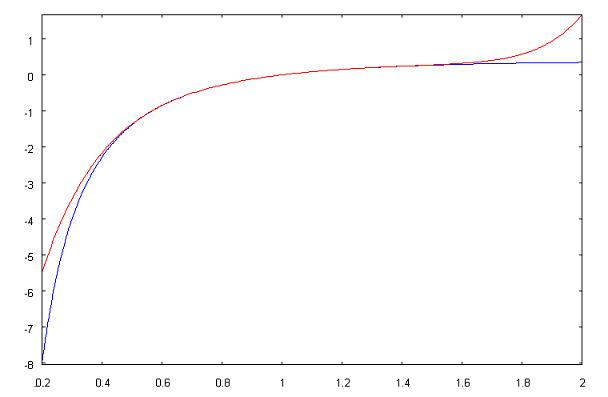
Мы видим,что красныйи синийграфикисливаютсяв окрестности

точки

x =1иудаляютсядруготдругаприудаленииаргументаотзначения1.

Этосвидетельствуетотом,чточастныесуммырядовТейлораприближают

функцию тольков окрестноститочки

x =1.

 

ТригонометрическиерядыФурье

 

 

Вразличныхотрасляхнауки,втомчисле,вфизикеприходитсяиметьдело с периодическимиявлениями.Простейшийпример– электрические

колебания. Периодической называется функция

f (x), для которой

существует такая величина,называемая периодом, что

f (x)=

f (x + T).

Простейшими T - периодическими функциями являются

 

тригонометрическиефункциивида

sin2p kx,cos2p kx,где k –целоечисло,

T T

называемые гармониками. Представлениепериодическойфункцииввиде

суммыгармоникназываетсягармоническиманализом.Вслучае,когдатакая

 

суммабесконечна,мыполучаемтригонометрическийряд, называемыйрядомФурье.

 

Итак, пусть непрерывная T - периодическая функция

f (x)

представлена в виде тригонометрического ряда:

å

f (x)= a 0+ ¥ a

cos2p kx + b

sin2p kx. Возникает вопрос: как найти

2 k =1 k

T k T

коэффициенты

a 0, ak, bk,

k Î N?

Воспользуемся тем,что гармоникиобладают следующимсвойством:

T /2

ò

- T /2

T /2

ò

- T /2

T /2

 

cos

 

sin

2p kx T

 

2p kx T

 

dx = 0,

 

 

dx = 0,

 

ò

- T /2

T /2

ò

- T /2

T /2

ò

- T /2

T /2

ò

cos2p lx sin2p mxdx = 0,

T T

 

cos2p lx cos2p mxdx = 0,

T T

 

sin2p lx sin2p mxdx = 0,

T T

 

cos22p lxdx = 2,

 

" l, m Î N,

 

 

" l, m ÎN, l ¹ m,

 

 

" l, m Î N, l ¹ m,

 

- T /2

T /2

ò

- T /2

T T

 

sin22p lxdx = 2.

T T

 

Теперьдлятого,чтобы,например,найтиравенства

am умножимобечасти

å

f (x)= a 0+ ¥ a

cos2p kx + b

sin2p kx

на cos2p mx

 

ипроинтегрируем

2 k =1 k

T k T T

наотрезке[- T /2, T /2].Сучетомсвойствгармониквправойчастиравенства

 

останется только слагаемое

a 2, а в левой части – выражение

m

T

T /2

ò

- T /2

 

f (x)cos

2p mx T

 

dx. Отсюдамыполучим

 

am.

Умножаянаsin2p mx

T

 

иинтегрируя,получим bm.

 

Адлятого,чтобыполучить

a 0,нужнопростопроинтегрироватьобе

 

части равенства

f (x)= a 0+ ¥ a

cos2p kx + b

sin2p kx

 

на отрезке

 

 

å

[- T /2, T /2].

2 k =1 k

T k T

 

Таким образом, непрерывная периодическая функцияпредставима в видеследующеготригонометрическогорядаФурье:

f (x)

å

f (x)= a 0+ ¥ a

cos2p kx + b

sin2p kx, где

2 T /2

 

k =1

k T k T

 

2p kx

ak = T

ò

- T /2

f (x)cos T

dx,

k = 0,1,2,....,

b = 2

k T

T /2

ò

- T /2

 

f (x)sin

2p kx T

 

dx,

 

k =1,2,....

 

Вслучае,когдапериодическаяфункцияимеет точкиразрыва,еетакжеможнораскладыватьврядФурье,норавенствофункцииисуммырядабудеттольковточкахнепрерывностифункции.ВточкахразрыварядФурьебудетсходитьсякполусуммезначенийфункциислеваисправаотточкиразрыва:

¥

a 0+ å a

cos2p kx 0+ b

sin2p kx 0= 1(f (x

- 0)+ f (x

+ 0)).

2 k =1 k

T k T 2 0 0

 

ВозможноразложениефункцииврядФурьеспомощьюMAXIMы.Мы

получимвсе коэффициентырядаФурье дляфункции

f (x), заданнойна

отрезке[- T, T ]

и T -периодическипродолженнойнавсювещественнуюось,

если введем load(fourie); fourier (f(x),x,t) и нажмемShift+Enter.

Пример. Получим коэффициенты ряда Фурье для функции

f (x)= ex,-p £ x < p. Для этого введем load(fourie);fourier(%e^x,x,%pi),

нажмем Shift+Enterи получим

a = (e p

- e -p

)/p,

an = (n sinp n /(e p n 2+ e p)+ e p n sinp n /(n 2+1)-

-cosp n /(e p n 2+ e p)+ e p cosp n /(n 2+1))/p,

bn = (sinp n /(e p n 2+ e p)+ e p p sinp n /(n 2+1)-

- n cosp n /(e p n 2+ e p)+ e p n cosp n /(n 2+1))/p.

 

Мы видим,что коэффициентысодержатвыражения sinp n = 0и

cosp n = (-1) n. Поэтомупреобразуемкоэффициенты:

 

 

a 0=

e p - e -p,

p

n

a = (-1) (1

e p),

-

n p e p (n 2+1) (n 2+1)

n

b = (-1) n (- 1

e p).

+

n p e p (n 2+1) (n 2+1)

 

Длятого,чтобынетольковычислитькоэффициентырядаФурье,нои

получитьразложениефункции

f (x), заданнойна отрезке[- T, T ]

и T -

периодическипродолженной на всювещественную ось врядФурье, следуетввести load(fourie);totalfourier(f(x),x,T) и нажать Shift+Enter.

 

 

Пример. ДляразложенияврядФурьефункцииизпредыдущегопримеравведем load(fourie);totalfourier(%e^x,x,%pi). Приэтомполучимразложение

¥

e -p (e p -1)(e p +1)å

– n =1

n (-1) n sin nx

n 2+1

¥

e -p (e p -1)(e p +1)å

+ n =1

(-1) n cos nx

n 2+1 +

p p

+ e -p (e p -1)(e p +1)

2p.

 

Следует отметить, что частные суммы ряда Фурье приближаютисходнуюфункциюне в конкретныхточках,а «всреднемпо отрезку».

Сравнимзаданнуюфункцию

y = ex,-p £ x £ p,и9-ючастнуюсуммуряда

Фурье на одном графике. Для этого сначала введем функцию

g (x),

совпадающуюс9-йчастнойсуммой,азатемнарисуемфункцию ex

(черным

цветом)ифункцию

[-p,p ]:

g (x)

(краснымцветом)наодномграфикенадотрезком

g(x):=-(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum((n*(-

1)^n*sin(n*x))/(n^2+1),n,1,9))/%pi+(%e^(-%pi)*(%e^%pi-

1)*(%e^%pi+1)*sum(((-1)^n*cos(n*x))/(n^2+1),n,1,9))/%pi+

(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1))/(2*%pi);

load(draw); draw2d(explicit(%e^x,x,-%pi,%pi), color=red,explicit(g(x),x,-%pi,%pi)).

 

 

В результате получимкартину

 

 

 

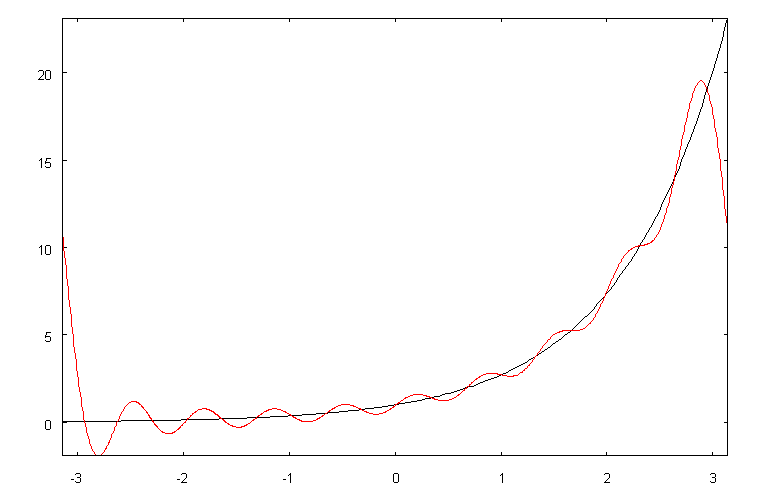
Здесь видно, что в конечных точках отрезка, где функция

y = ex,-p £ x £ p, припериодическомпродолжениис отрезка [-p,p ] в

другиеточкивещественнойоситерпитразрыв,графикчастнойсуммырядаФурье(краснаялиния)значительноотличаетсяотграфикаэкспоненциальнойфункции.Еслибратьчастнуюсуммусбольшимколичествомчленов,тографикчастнойсуммыбудеттеснееприближатьсякисходнойфункцииво

внутреннихточкахинтервала (-p,p),новблизиточек x = ±p

поведение

будет тем же из-за разрыва исходной функции при периодическомпродолжении.

 

 

ДИФФЕРЕНЦИАЛЬНЫЕУРАВНЕНИЯ

 

 

Дифференциальным уравнением называется соотношение вида

F (x, y (x), y ¢, y ¢,..., y (n))= 0. Решить дифференциальное уравнение – это

значит,определитьфункцию

y (x),удовлетворяющееэтомусоотношению,

возможно, в неявном или параметрическомвиде.

Простейшеедифференциальноеуравнениевида

 

 

y ¢(x)=

 

 

f (x)

 

 

мы уже

 

решали, так как находили

y (x)= ò f (x) dx. Мы знаем, что интеграл

определяетсясточностьюдопроизвольногопостоянногослагаемого.Тоесть

решение простейшего дифференциального уравнения содержит

 

произвольнуюпостоянную.Решенияболеесложныхдифференциальныхуравненийтакженаходятсясточностьюдопроизвольныхпостоянных.Любуюфункцию,удовлетворяющуюдифференциальномууравнению,мыбудемназывать частнымрешением этогоуравнения,совокупностьчастныхрешенийназовем общимрешением дифференциальногоуравнения.

Порядок дифференциального уравнения определяетсянаивысшимпорядком входящих в него производных. Поэтому дифференциальное

уравнениевида

F (x, y (x), y ¢, y ¢,..., y (n))= 0

считаетсядифференциальным

уравнением n -гопорядка.

Также,какнелюбаяфункцияможетбытьпроинтегрирована,ипредставленаввидеэлементарныхфункций,такинелюбоедифференциальноеуравнениеимеетрешение,выражающеесячерезэлементарныефункции.Классдифференциальныхуравнений,

интегрируемыхв квадратурах,узок.Мы изучимнесколькоклассов

дифференциальныхуравнений,интегрируемыхвквадратурах,атакжерассмотримн