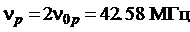Мы рассмотрим физическую реализацию кубита на примере квантовой системы со спиновым магнитным резонансом.
На основе уравнения Дирака можно показать, что наличие спина у электрона приводит к появлению у него магнитного момента. Соответствующий гамильтониан взаимодействия магнитного момента 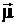 с магнитным полем
с магнитным полем 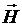 есть:
есть:
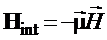 , где
, где 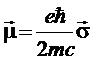
Пусть магнитное поле 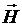 есть комбинация однородного поля
есть комбинация однородного поля 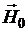 , направленного вдоль оси
, направленного вдоль оси 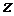 и поля
и поля 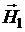 , вращающегося в плоскости
, вращающегося в плоскости  :
:

Для определенности будем иметь ввиду электрон. С учетом отрицательного знака заряда электрона, имеем:
 , где
, где 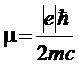
Уравнение Паули, представляющее собой модификацию уравнения Шредингера с учетом спина электрона, есть:
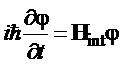 ,
,
где  - двухкомнонетнный спинор.
- двухкомнонетнный спинор.
Пусть  ,
,  - соответственно продольная и поперечная частоты.
- соответственно продольная и поперечная частоты.
Тогда уравнение Паули примет вид:
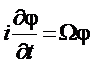 ,
,
где  - оператор частоты.
- оператор частоты.
Осуществим переход к другим (медленным) переменным посредством преобразования

Рассматриваемое преобразование называется переходом во вращающуюся систему координат. Для новой переменной получим уравнение:

Учтем, что (см. формулу (4.4) раздела 4.2):
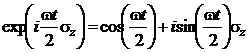
Тогда, рассматриваемое уравнение примет вид:

Его решение, очевидно, есть:
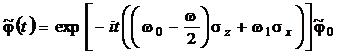
Последняя формула описывает поворот квантового состояния на сфере Блоха.
Ось поворота и угол вращения есть:
 ,
,  ,
,
Где  - частота Раби
- частота Раби
Наиболее простая динамика спина- кубита будет наблюдаться в условиях резонанса, когда
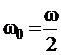 . Практически такой резонанс достигается обычно путем медленного изменения продольного поля
. Практически такой резонанс достигается обычно путем медленного изменения продольного поля  .
.
В условиях резонанса в рассматриваемом примере происходит вращение состояния кубита вокруг оси 
Задача 4.18 Пусть начальное состояние кубита есть  , что соответствует «северному полюсу» на сфере Блоха. Покажите, что в условиях резонанса, чтобы перевести кубит из состояния
, что соответствует «северному полюсу» на сфере Блоха. Покажите, что в условиях резонанса, чтобы перевести кубит из состояния 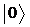 в состояние
в состояние 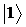 , достаточно выждать в течении времени
, достаточно выждать в течении времени  (так называемый
(так называемый 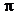 - импульс). Аналогично, покажите, что воздействие в течении
- импульс). Аналогично, покажите, что воздействие в течении  приводит к повороту состояния на угол
приводит к повороту состояния на угол 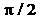 вокруг оси
вокруг оси  , что соответствует преобразованию состояния
, что соответствует преобразованию состояния  в состояние
в состояние 
Динамика кубита может быть представлена в виде:
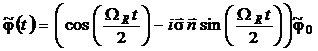
Задача 4.19 Пусть начальное состояние кубита есть  . Покажите, что вероятность переворота спина (спин- флип) есть:
. Покажите, что вероятность переворота спина (спин- флип) есть:
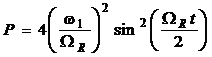
Среднее по времени от полученной вероятности есть:

Последнее выражение, рассматриваемое как функция  , описывает резонанс на частоте
, описывает резонанс на частоте  .
.
Заметим, что в реальных экспериментах, как правило, 
Приведём некоторые данные, необходимые для проведения численных оценок
Магнитный момент электрона:
 , где
, где
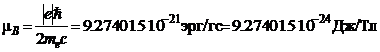 - магнетон Бора.
- магнетон Бора.
Небольшое отличие отношения 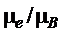 от единицы называется аномальным магнитным моментом электрона. Теоретическое объяснение этого эффекта, согласующееся с экспериментом с очень высокой точности, является важным достижением квантовой электродинамики.
от единицы называется аномальным магнитным моментом электрона. Теоретическое объяснение этого эффекта, согласующееся с экспериментом с очень высокой точности, является важным достижением квантовой электродинамики.
Магнитный момент протона есть:
 , где
, где
 - ядерный магнетон
- ядерный магнетон
Большое отличие магнитного момента протона от ядерного магнетона является следствием сложной (кварковой) структуры частицы (заметим, что в теории Дирака частица предполагается точечной).
Нейтрон, несмотря на нулевой заряд, также обладает магнитным моментом, который равен (в ядерных магнетонах)
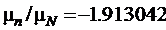
Оценим типичные частоты, возникающие при магнитном резонансе
Пусть продольное поле есть: 
Тогда для электрона получаем: 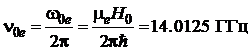 ,
,
Резонансная частота есть: 
Аналогично для протона:
 ,
,
Резонансная частота протона: 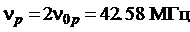





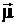 с магнитным полем
с магнитным полем 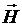 есть:
есть: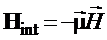 , где
, где 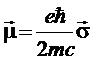
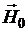 , направленного вдоль оси
, направленного вдоль оси 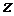 и поля
и поля 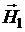 , вращающегося в плоскости
, вращающегося в плоскости  :
:
 , где
, где 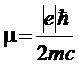
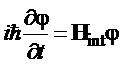 ,
, - двухкомнонетнный спинор.
- двухкомнонетнный спинор. ,
,  - соответственно продольная и поперечная частоты.
- соответственно продольная и поперечная частоты.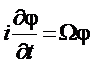 ,
, - оператор частоты.
- оператор частоты.

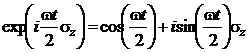

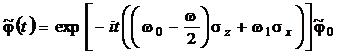
 ,
,  ,
, - частота Раби
- частота Раби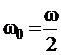 . Практически такой резонанс достигается обычно путем медленного изменения продольного поля
. Практически такой резонанс достигается обычно путем медленного изменения продольного поля 
 , что соответствует «северному полюсу» на сфере Блоха. Покажите, что в условиях резонанса, чтобы перевести кубит из состояния
, что соответствует «северному полюсу» на сфере Блоха. Покажите, что в условиях резонанса, чтобы перевести кубит из состояния 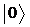 в состояние
в состояние 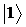 , достаточно выждать в течении времени
, достаточно выждать в течении времени  (так называемый
(так называемый 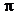 - импульс). Аналогично, покажите, что воздействие в течении
- импульс). Аналогично, покажите, что воздействие в течении  приводит к повороту состояния на угол
приводит к повороту состояния на угол 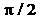 вокруг оси
вокруг оси 
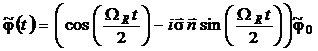
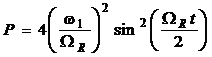

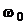 , описывает резонанс на частоте
, описывает резонанс на частоте  .
.
 , где
, где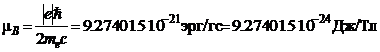 - магнетон Бора.
- магнетон Бора.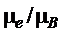 от единицы называется аномальным магнитным моментом электрона. Теоретическое объяснение этого эффекта, согласующееся с экспериментом с очень высокой точности, является важным достижением квантовой электродинамики.
от единицы называется аномальным магнитным моментом электрона. Теоретическое объяснение этого эффекта, согласующееся с экспериментом с очень высокой точности, является важным достижением квантовой электродинамики. , где
, где - ядерный магнетон
- ядерный магнетон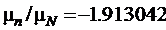

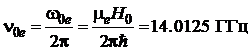 ,
,
 ,
,