Неравенство, предложенное Шредингером и Робертсоном, отражает в себе свойства, присущие как неравенству Коши- Буняковского, так и соотношению неопределенностей Гейзенберга и, в известном смысле, может считаться их обобщением [35,36].
Пусть  и
и  - две произвольные наблюдаемые. Без ограничения общности будем считать их центрированными:
- две произвольные наблюдаемые. Без ограничения общности будем считать их центрированными:  .
.
Рассмотрим следующее заведомо неотрицательное выражение:

Здесь  - произвольное действительное число,
- произвольное действительное число, 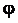 - тоже действительное, но фиксированное число (фаза, выбор которой мы осуществим позднее).
- тоже действительное, но фиксированное число (фаза, выбор которой мы осуществим позднее).
Определим ковариацию величин как

Заметим, что симметризация произведения наблюдаемых потребовалась нам, чтобы сделать соответствующий оператор эрмитовым.
Пусть:
 ,
,
где 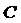 - эрмитов оператор. Тогда:
- эрмитов оператор. Тогда:
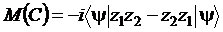
В развернутой записи выражение для  имеет вид:
имеет вид:

Пусть:
 ,
,
Очевидно, можно найти такой угол  , чтобы выполнялись тождества:
, чтобы выполнялись тождества:
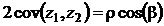

Тогда:

Распорядимся произволом в выборе фазы 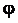 , чтобы обеспечить выполнение равенства
, чтобы обеспечить выполнение равенства  . Указанный выбор, очевидно, обеспечит получение наиболее сильного неравенства:
. Указанный выбор, очевидно, обеспечит получение наиболее сильного неравенства:

Определим коэффициент корреляции между наблюдаемыми  и
и  как:
как:

В результате, искомое неравенство (соотношение неопределенностей Шредингера- Робертсона) примет вид:
 ,
,
где 
Введенный параметр 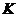 есть аналог известного числа Шмидта [37]. Это число имеет фундаментальное значение для описания квантовых корреляций и квантовой информации (см. Приложение к Главе 3).
есть аналог известного числа Шмидта [37]. Это число имеет фундаментальное значение для описания квантовых корреляций и квантовой информации (см. Приложение к Главе 3).
Пусть теперь рассматриваемые наблюдаемые есть операторы координаты и импульса соответственно:
 ,
,  .
.
Тогда, в силу фундаментального перестановочного соотношения для координаты и импульса, 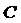 есть тождественный оператор (единичная матрица).
есть тождественный оператор (единичная матрица).
В этом случае соотношение неопределенностей Шредингера- Робертсона будет иметь вид:

Пусть  ,
,  - неопределенности (стандартные отклонения) для координаты и импульса. Тогда:
- неопределенности (стандартные отклонения) для координаты и импульса. Тогда:

Таким образом, если координата и импульс коррелируют друг с другом, произведение их неопределенностей возрастает в  раз по сравнению с величиной, определяемой неравенством Гейзенберга.
раз по сравнению с величиной, определяемой неравенством Гейзенберга.
Заметим, что в силу некоммутативности координаты и импульса, их квантовая ковариация не может быть оценена по выборке подобно классической ковариации. Для вычисления соответствующей оценки нужно знать априори (или оценить по результатам взаимно- дополнительных измерений) вектор состояния (волновую функцию). Пусть:
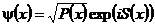 ,
,
где действительные функции 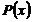 и
и  есть соответственно плотность и фаза пси- функции. Заметим, что фаза
есть соответственно плотность и фаза пси- функции. Заметим, что фаза  есть аналог классического действия механической системы.
есть аналог классического действия механической системы.
Используя функции плотности и фазы, нетрудно получить следующее простое представление для ковариации координаты и импульса:

Наглядность полученного результата обусловлена тем, что в классической механике производная от функции действия  есть импульс.
есть импульс.





 и
и  - две произвольные наблюдаемые. Без ограничения общности будем считать их центрированными:
- две произвольные наблюдаемые. Без ограничения общности будем считать их центрированными:  .
.
 - произвольное действительное число,
- произвольное действительное число, 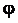 - тоже действительное, но фиксированное число (фаза, выбор которой мы осуществим позднее).
- тоже действительное, но фиксированное число (фаза, выбор которой мы осуществим позднее).
 ,
,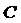 - эрмитов оператор. Тогда:
- эрмитов оператор. Тогда: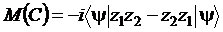
 имеет вид:
имеет вид:
 ,
, , чтобы выполнялись тождества:
, чтобы выполнялись тождества: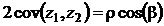


 . Указанный выбор, очевидно, обеспечит получение наиболее сильного неравенства:
. Указанный выбор, очевидно, обеспечит получение наиболее сильного неравенства:

 ,
,
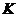 есть аналог известного числа Шмидта [37]. Это число имеет фундаментальное значение для описания квантовых корреляций и квантовой информации (см. Приложение к Главе 3).
есть аналог известного числа Шмидта [37]. Это число имеет фундаментальное значение для описания квантовых корреляций и квантовой информации (см. Приложение к Главе 3). ,
,  .
.
 ,
,  - неопределенности (стандартные отклонения) для координаты и импульса. Тогда:
- неопределенности (стандартные отклонения) для координаты и импульса. Тогда:
 раз по сравнению с величиной, определяемой неравенством Гейзенберга.
раз по сравнению с величиной, определяемой неравенством Гейзенберга.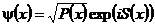 ,
,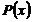 и
и  есть соответственно плотность и фаза пси- функции. Заметим, что фаза
есть соответственно плотность и фаза пси- функции. Заметим, что фаза 
 есть импульс.
есть импульс.


