Свойства характеристической функции позволяют ввести оператор координаты в импульсном представлении. Действительно, рассматривая характеристическую функцию как свертку (1.5), имеем

Таким образом, если в координатном представлении координата описывается оператором  , сводящимся к умножению пси- функции на число
, сводящимся к умножению пси- функции на число  , (т.е.
, (т.е. 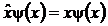 ), то в импульсном представлении оператор координаты есть
), то в импульсном представлении оператор координаты есть  .
.
Аналогичным образом нетрудно показать, что, если в импульсном представлении импульс описывается оператором  , просто сводящимся к умножению пси- функции на число
, просто сводящимся к умножению пси- функции на число 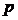 , т.е.
, т.е.  , то в координатном представлении оператор импульса есть
, то в координатном представлении оператор импульса есть  (изменение знака перед мнимой единицей
(изменение знака перед мнимой единицей 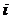 соответствует отличию между прямым и обратным преобразованиями Фурье).
соответствует отличию между прямым и обратным преобразованиями Фурье).
Заметим, что операторы координаты и импульса эрмитовы. Переход от координатного представления к импульсному оставляет инвариантным фундаментальное коммутационное соотношение:
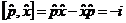
В случае нескольких степеней свободы представленное каноническое соотношение примет вид
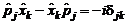 ,
, 
Здесь 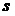 - число степеней свободы
- число степеней свободы
Рассматриваемое соотношение показывает, что каждый импульс не коммутирует только со своей (канонически сопряженной) координатой и коммутирует со всеми остальными координатами.
Все координаты коммутируют между собой, так же как и все импульсы коммутируют между собой

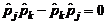
Преобразование, сохраняющее фундаментальные коммутационные соотношения, называются каноническими.
Преобразование Фурье является частным случаем унитарных преобразований. Оказывается, что в квантовой информатике можно рассматривать произвольные унитарные преобразования. При этом будет происходить замена одного представления на другое, дополнительное по отношению к исходному. Измерения, проводимые в различных представлениях, порождают совокупность взаимно- дополнительных распределений. Рассмотренные соображения, изложенные систематическим образом, являются основой постулатов квантовой информатики (см. главу 3).
Приложение 1. Дельта- функция и ее свойства.
Мы приведем только краткую сводку некоторых важных свойств дельта- функции. Более полное и строгое изложение вопроса можно найти в [34].
Дельта- функция является важным инструментом в квантовой информатике, поскольку находит широкое применение в таких вопросах, как теория преобразования Фурье, статистический анализ взаимно- дополнительных распределений и др.
Проведем исследования выражения (1.3) из раздела 1.1:
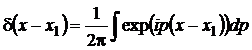 (П1.1)
(П1.1)
В точке 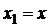 рассматриваемый интеграл заведомо расходится. Проведем его регуляризацию. Ограничим область интегрирования по переменной
рассматриваемый интеграл заведомо расходится. Проведем его регуляризацию. Ограничим область интегрирования по переменной  в пределах от
в пределах от  до
до  . Регуляризованная версия исходного соотношения (П1.1) есть
. Регуляризованная версия исходного соотношения (П1.1) есть
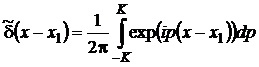
Элементарное интегрирование сразу приводит к результату:

Заметим, что интеграл от полученной функции по переменной 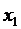 всегда равен единице:
всегда равен единице:
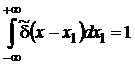
Проанализируем характер поведения рассматриваемой функции  . Её максимум находится в точке
. Её максимум находится в точке 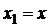 и равен
и равен  . При больших значениях обрезающего множителя
. При больших значениях обрезающего множителя  рассматриваемая функция локализована внутри интервала порядка
рассматриваемая функция локализована внутри интервала порядка  . При увеличении
. При увеличении  функция становится все более и более локализованной вблизи ноля.
функция становится все более и более локализованной вблизи ноля.
Последовательность функций  , отвечающая бесконечно растущей последовательности значений
, отвечающая бесконечно растущей последовательности значений  , называется дельта-образной. Дельта-функцию можно определить как обобщенную сингулярную предельную функцию дельта-образной последовательности.
, называется дельта-образной. Дельта-функцию можно определить как обобщенную сингулярную предельную функцию дельта-образной последовательности.
Таким образом,

Приведем также некоторые другие представления для дельта- функции:
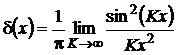 (П1.2)
(П1.2)
 (П1.3)
(П1.3)
Задача П1.1 Обоснуйте представления (П1.2) и (П1.3) для дельта- функции.
Дельта- функция может рассматриваться как производная от ступенчатой функции (функции Хевисайда)
 , где
, где
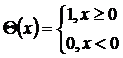
Основное свойство дельта- функции определяет способ ее интеграции с произвольной несингулярной функцией:

Нетрудно получить и некоторые другие свойства для дельта- функции
 (П1.4)
(П1.4)
 (П1.5)
(П1.5)
 , (П1.6)
, (П1.6)
где  - простые корни функции
- простые корни функции 
Задача П1.2. Обоснуйте приведенные формулы (П1.4)- (П1.6).






 , сводящимся к умножению пси- функции на число
, сводящимся к умножению пси- функции на число  , (т.е.
, (т.е. 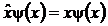 ), то в импульсном представлении оператор координаты есть
), то в импульсном представлении оператор координаты есть  .
. , просто сводящимся к умножению пси- функции на число
, просто сводящимся к умножению пси- функции на число 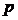 , т.е.
, т.е.  , то в координатном представлении оператор импульса есть
, то в координатном представлении оператор импульса есть  (изменение знака перед мнимой единицей
(изменение знака перед мнимой единицей 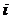 соответствует отличию между прямым и обратным преобразованиями Фурье).
соответствует отличию между прямым и обратным преобразованиями Фурье).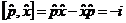
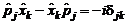 ,
, 
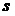 - число степеней свободы
- число степеней свободы
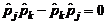
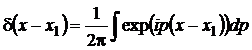 (П1.1)
(П1.1)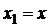 рассматриваемый интеграл заведомо расходится. Проведем его регуляризацию. Ограничим область интегрирования по переменной
рассматриваемый интеграл заведомо расходится. Проведем его регуляризацию. Ограничим область интегрирования по переменной  в пределах от
в пределах от  до
до  . Регуляризованная версия исходного соотношения (П1.1) есть
. Регуляризованная версия исходного соотношения (П1.1) есть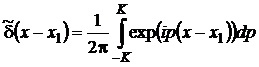

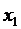 всегда равен единице:
всегда равен единице: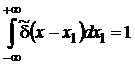
 . Её максимум находится в точке
. Её максимум находится в точке  . При больших значениях обрезающего множителя
. При больших значениях обрезающего множителя  . При увеличении
. При увеличении 
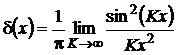 (П1.2)
(П1.2) (П1.3)
(П1.3) , где
, где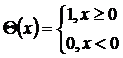

 (П1.4)
(П1.4) (П1.5)
(П1.5) , (П1.6)
, (П1.6) - простые корни функции
- простые корни функции 



