Рассматриваемое неравенство имеет место для векторов произвольных линейных пространств, в которых определено понятие скалярного произведения. Приведем примеры таких пространств.
В комплексном конечномерном пространстве 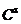 размерности
размерности 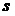 скалярное произведение двух векторов определяется следующей формулой (в обозначениях Дирака):
скалярное произведение двух векторов определяется следующей формулой (в обозначениях Дирака):
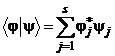
В бесконечномерном гильбертовом пространстве  аналогичное определение имеет вид:
аналогичное определение имеет вид:
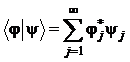
Наконец, если 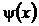 и
и 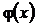 - комплексные функции из пространства
- комплексные функции из пространства  , то их скалярное произведение есть:
, то их скалярное произведение есть:

Покажем, что для любых векторов линейного пространства со скалярным произведением выполняется следующее неравенство Коши- Буняковского:
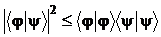
Для определенности, при проведении выкладок будем иметь ввиду функции из пространства  .
.
Предположим вначале, что скалярное произведение 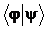 - действительное число.
- действительное число.
Пусть  - действительный параметр. Рассмотрим следующую заведомо неотрицательную функцию от
- действительный параметр. Рассмотрим следующую заведомо неотрицательную функцию от  (эта функция представляет собой интеграл от заведомо неотрицательного выражения).
(эта функция представляет собой интеграл от заведомо неотрицательного выражения).
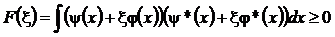
В обозначениях Дирака имеем:
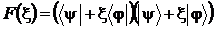
В развернутой записи рассматриваемая функция представляет собой квадратный трехчлен:
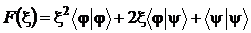
Здесь мы учли предположение о действительности рассматриваемого скалярного произведения, т.е. 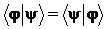 .
.
Условие неотрицательности означает, что дискриминант меньше или равен нулю:

Таким образом в рассматриваемом случае выполняется неравенство Коши- Буняковского:
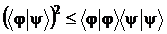
Предположим теперь, что 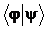 - комплексное число. Пусть
- комплексное число. Пусть 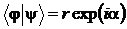 , где
, где 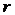 и
и  - действительные числа.
- действительные числа.
Введем функцию, отличающуюся от 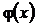 только фазой
только фазой
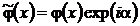
Тогда 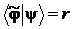 является действительным числом и для него выполняется доказанное выше неравенство:
является действительным числом и для него выполняется доказанное выше неравенство:

Учтем, что введенное фазовое преобразование не меняет модуля скалярного произведения, поэтому:  ,
, 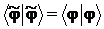 .
.
Таким образом, неравенство Коши- Буняковского выполняется и в общем случае:
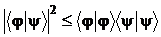
Введем величину 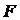 , называемую согласованностью (fidelity) квантовых состояний
, называемую согласованностью (fidelity) квантовых состояний 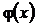 и
и 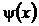 .
.
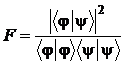
Для состояний, нормированных на единицу, имеем просто:
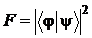
Из неравенства Коши- Буняковского следует, что

Если исходить из этого неравенства, то заманчиво предположить, что 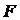 задает некоторую вероятность. Так оно и есть. Статистический смысл величины
задает некоторую вероятность. Так оно и есть. Статистический смысл величины 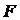 заключается в том, что она задает вероятность обнаружения квантовой системы в состоянии
заключается в том, что она задает вероятность обнаружения квантовой системы в состоянии 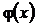 при условии, что она была приготовлена в состоянии
при условии, что она была приготовлена в состоянии 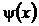
Обмен информацией в природе предполагает, что состояние 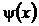 , приготовленное (созданное) на одном конце (в системе «передатчик») может быть обнаружено (воспринято) таковым в другой системе-«приёмнике». В идеальном случае «приемник» может быть настроен на получение того же квантового состояния, когда
, приготовленное (созданное) на одном конце (в системе «передатчик») может быть обнаружено (воспринято) таковым в другой системе-«приёмнике». В идеальном случае «приемник» может быть настроен на получение того же квантового состояния, когда 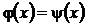 (с точностью до фазового множителя). В этом случае
(с точностью до фазового множителя). В этом случае  . В действительности состояния
. В действительности состояния 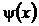 и
и 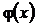 , на которые настроен приемник и передатчик соответственно, всегда хотя бы немного отличаются и
, на которые настроен приемник и передатчик соответственно, всегда хотя бы немного отличаются и 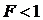 . В рассматриваемом случае, таким образом,
. В рассматриваемом случае, таким образом, 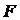 задает вероятность «успеха» приемно- передающего акта.
задает вероятность «успеха» приемно- передающего акта.





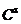 размерности
размерности 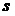 скалярное произведение двух векторов определяется следующей формулой (в обозначениях Дирака):
скалярное произведение двух векторов определяется следующей формулой (в обозначениях Дирака):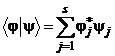
 аналогичное определение имеет вид:
аналогичное определение имеет вид: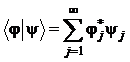
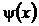 и
и 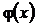 - комплексные функции из пространства
- комплексные функции из пространства  , то их скалярное произведение есть:
, то их скалярное произведение есть:
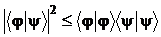
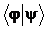 - действительное число.
- действительное число. - действительный параметр. Рассмотрим следующую заведомо неотрицательную функцию от
- действительный параметр. Рассмотрим следующую заведомо неотрицательную функцию от 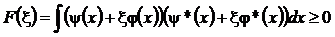
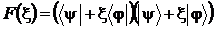
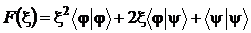
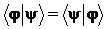 .
.
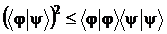
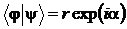 , где
, где 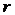 и
и  - действительные числа.
- действительные числа.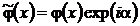
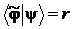 является действительным числом и для него выполняется доказанное выше неравенство:
является действительным числом и для него выполняется доказанное выше неравенство:
 ,
, 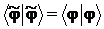 .
. , называемую согласованностью (fidelity) квантовых состояний
, называемую согласованностью (fidelity) квантовых состояний 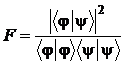
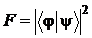

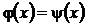 (с точностью до фазового множителя). В этом случае
(с точностью до фазового множителя). В этом случае  . В действительности состояния
. В действительности состояния 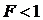 . В рассматриваемом случае, таким образом,
. В рассматриваемом случае, таким образом, 


