Технологические процессы обработки металлов давлением оцениваются многими критериями. Многокритериальность свидетельствует о неопределенности целей. Стремление технолога добиться того, чтобы поковка была максимально точной, обладала высокими механическими свойствами, была дешевой при малой изнашиваемости штампов и оборудования, не всегда осуществимо. Применение одного критерия в качестве целевой функции может дать неправильную оценку процессу. Поэтому реальное решение всегда будет компромиссом.
Определение множества целей, степень достижения которых предстоит оценивать, базируется на анализе оцениваемого процесса. При этом предполагается приведение всех вариантов к тождественному эффекту.
При оценке технологического процесса наиболее удобно использовать граф целей и задач. Цели любого уровня могут рассматриваться как задачи, решение которых приводит к достижению целей вышестоящего уровня. Для построения графа целей и задач проектирования технологического процесса обработки давлением необходимо на основе анализа этого процесса определить множество целей различных рангов. Например, целью нулевого ранга F0 выбирается оптимальный технологический процесс. Далее можно выделить три цели первого ранга: F11 – качество изделия, F12 – технический уровень технологического процесса, F13 – приведенные затраты. Цели следующего ранга определяются конкретным видом и назначением поковки. Дальнейшие цели учитывают коэффициент использования металла, производительность, степень автоматизации производства, стойкость инструмента и т.д.
Целям технологического процесса ставятся в соответствие критерии их достижения. Для проектируемых процессов критерии определяют по прототипам и аналогам либо имитационным моделированием.
Решением многокритериальной задачи оптимизации является выбор предпочтительного варианта технологического процесса на основе установленных оценок для критериев.
Выбор оптимального технологического процесса со многими критериями относится к классу задач принятия решения, который характеризуется множеством целей и множеством вариантов их достижения. Задача нахождения наилучшего решения на множестве целей (задача многоцелевой оптимизации) формулируется следующим образом.
Пусть х – решение, определенное на множестве Х возможных способов достижения поставленных целей. Элементы х 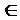 Х называются допустимыми решениями, вариантами решений, альтернативами и так далее. Каждое решение приводит к результату, последствия которого оцениваются набором из n скалярных критериев W1(x),..., Wn(x), характеризующих эффективность достижения целей. Вектор W = (W1,...,Wn) связан с решением х
Х называются допустимыми решениями, вариантами решений, альтернативами и так далее. Каждое решение приводит к результату, последствия которого оцениваются набором из n скалярных критериев W1(x),..., Wn(x), характеризующих эффективность достижения целей. Вектор W = (W1,...,Wn) связан с решением х 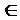 Х отображением, определяемым как векторное произведение:
Х отображением, определяемым как векторное произведение:
W0 = W*1 ´ W*2 ´... ´ W*n (2.9.1)
где W*i (i =1,..., n) – множество допустимых значений i–го частного критерия.
Необходимо найти такое допустимое и наилучшее решение 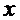 0
0 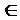 Х, которое оптимизирует эффективность W(х).
Х, которое оптимизирует эффективность W(х).
Модель оптимизации имеет вид:
W(х0)= opt W(х), х 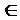 Х (2.9.2)
Х (2.9.2)
где opt– оператор оптимизации, определяющий в явном виде принцип выбора наилучшего решения из всех допустимых.
Идеальным решением называется такое, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Как правило, это множество пустое, так как между критериями существуют противоречия. Улучшение решения по одному из критериев вызывает ухудшение по другому или совокупности критериев. В связи с этим возникают задачи: выявление области компромисса; установление принципа, определяющего выбор наилучшего решения среди множества допустимых; построение математической или логической модели, реализующей принятый в задаче принцип оптимальности.
Для решения первой задачи из области допустимого множества решений Х выделяют два непересекающихся множества: ХС 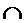 ХК = Æ. В первой области ХС, называемой областью согласия, все принадлежащие ей решения могут быть улучшены одновременно по всем частным критериям. Область ХК называется областью Парето, или областью компромисса, а решения, ей соответствующие, – эффективными. При любом выборе решения из этой области нужно заранее условиться о каком-то компромиссе, устанавливающем принцип выбора наилучшего решения.
ХК = Æ. В первой области ХС, называемой областью согласия, все принадлежащие ей решения могут быть улучшены одновременно по всем частным критериям. Область ХК называется областью Парето, или областью компромисса, а решения, ей соответствующие, – эффективными. При любом выборе решения из этой области нужно заранее условиться о каком-то компромиссе, устанавливающем принцип выбора наилучшего решения.
Одним из универсальных методов принятия решения при многих критериях является построение решающих правил, которые постулируют свертку частных критериев в один обобщенный критерий, называемый комплексным критерием (или функцией ценностей, функцией предпочтения, функцией полезности):
W0(x) = j [W1(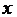 ),..., WN(
),..., WN(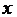 )] (2.9.3)
)] (2.9.3)
такой, что число W0(x) может служить оценкой эффективности. При предположении о независимости частных критериев обобщенный критерий представляется как аддитивная функция N переменных:
W0(x) = 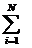 ji [Wi(x)]. (2.9.4)
ji [Wi(x)]. (2.9.4)
Функция ji[Wi(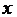 )] обеспечивает возможность учета нелинейного характера зависимости комплексного критерия от частных. Простейший способ построения комплексного критерия основан на линейной свертке частных критериев:
)] обеспечивает возможность учета нелинейного характера зависимости комплексного критерия от частных. Простейший способ построения комплексного критерия основан на линейной свертке частных критериев:
W0(x) = 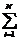 li [Wi(x)], (2.9.5)
li [Wi(x)], (2.9.5)
где li – положительные числа, в общем случае различные для всех i =1,..., N.
Применение линейной формы допустимо в качестве комплексного критерия, еслипространство критериев однородно, то есть когда критерии приведены к одной единице измерения или безразмерны. Комплексный критерий в аддитивной форме позволяет определять вклад каждого критерия Wi(x) в суммарную оценку эффективности. При использовании линейной формы необходимо установить границы изменения критериев, в пределах которых возможна линейная компенсация одних частных критериев за счет других.
Построение любого решающего правила и выбор принципа оптимальности требуют в задачах многокритериальной оптимизации привлечения лица, участвующего в принятии решения и способного с позиций оценки нескольких целей установить предпочтительность выбора вариантов решений. Однако в сложной ситуации выбора решения представления лица, принимающего решения, обычно оказываются неполными инечеткими. Они не позволяют ему априорно полностью проанализировать различные аспекты сравниваемых вариантов решений, установить их существенность, сформулировать целостное отношение к альтернативным вариантам.
Таким образом, методика решения многокритериальной задачи предусматривает следующие этапы:
анализ научно-технической и патентной литературы для назначения и ввода в модель конкретных значений параметров, которые подлежат дальнейшему уточнению;
замена нескольких критериев комплексным критерием, который включает в себя все используемые критерии; например,
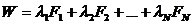 (2.9.6)
(2.9.6)
где li – весовые коэффициенты; величина li определяет значимость критерия Fi;вычисление li; для этого используют различные методы, но все они основаны на мнении экспертов.
Методы принятия решений облегчают процесс оптимизации, но не дают ответа относительно выбора конечного результата. Окончательный ответ остается прерогативой человека.
Вопросы по дисциплине
«Основы научных исследований, организация и планирование эксперимента»
1. Переход от одних единиц измерения к другим
2. Первая теорема подобия
3. Вторая теорема подобия. p–теорема
4. Формирование безразмерных комплексов p на основе размерностей
5. Корреляционный анализ опытных данных
6. Дисперсионный анализ опытных данных
7. Основные понятия и определения планирования эксперимента
8. План полного факторного эксперимента
9. Классификация планов эксперимента
10. Критерии оптимальности планов эксперимента.
11. Построение линейных и квазилинейных уравнений регрессии на базе планирования эксперимента
12. Проверка значимости коэффициентов линейных и квазилинейных моделей
13. Построение регрессионных моделей второго порядка
14. Регрессионный анализ
15. Оценка фактора времени при планировании эксперимента
16. Выбор лучшей модели по среднеквадратичной ошибке аппроксимации
17.. Критерий Уилкса выбора лучшей модели
18. Выбор лучшей модели по комплексной функции качества
19. Стратегия экспериментальной работы. Выбор объекта исследования, целевой функции, объема выборки, основного уровня и интервалов варьирования факторов
20. Особенности промышленного эксперимента
21. Организация контроля над выполнением программы экспериментальной работы.
22. Оценка завершенности экспериментальной работы



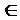 Х называются допустимыми решениями, вариантами решений, альтернативами и так далее. Каждое решение приводит к результату, последствия которого оцениваются набором из n скалярных критериев W1(x),..., Wn(x), характеризующих эффективность достижения целей. Вектор W = (W1,...,Wn) связан с решением х
Х называются допустимыми решениями, вариантами решений, альтернативами и так далее. Каждое решение приводит к результату, последствия которого оцениваются набором из n скалярных критериев W1(x),..., Wn(x), характеризующих эффективность достижения целей. Вектор W = (W1,...,Wn) связан с решением х 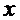 0
0 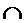 ХК = Æ. В первой области ХС, называемой областью согласия, все принадлежащие ей решения могут быть улучшены одновременно по всем частным критериям. Область ХК называется областью Парето, или областью компромисса, а решения, ей соответствующие, – эффективными. При любом выборе решения из этой области нужно заранее условиться о каком-то компромиссе, устанавливающем принцип выбора наилучшего решения.
ХК = Æ. В первой области ХС, называемой областью согласия, все принадлежащие ей решения могут быть улучшены одновременно по всем частным критериям. Область ХК называется областью Парето, или областью компромисса, а решения, ей соответствующие, – эффективными. При любом выборе решения из этой области нужно заранее условиться о каком-то компромиссе, устанавливающем принцип выбора наилучшего решения.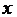 ),..., WN(
),..., WN(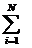 ji [Wi(x)]. (2.9.4)
ji [Wi(x)]. (2.9.4)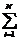 li [Wi(x)], (2.9.5)
li [Wi(x)], (2.9.5)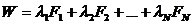 (2.9.6)
(2.9.6)

